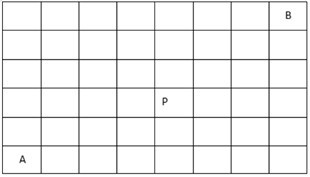
【组合数学+动态规划】在如下8*6的矩阵中，请计算从A移动到B一共有____种走法。要求每次只能向上或向右移动一格，并且不能经过P。

在如下8*6的矩阵中，请计算从A移动到B一共有__种走法。要求每次只能向上或向右移动一格，并且不能经过P。

A:456 
B:492 
C:568 
D:626 
E:680 
F:702

解析: 
8*6的矩阵，从左下角A到右上角B，一共需要走12步，其中5步向上，7步向右，因此总的走法一共有C(12,5)=792种，但题目规定不能经过P，因此需要减去经过P点的走法。 
经过P的路径分为两部分，从A到P，从P到B。 
同理，从A到P的走法：C(6,2)=15； 
同理，从P到B的走法：C(6,3)=20； 
因此从A到B经过P点的走法有15*20=300种， 
所以从A到B不经过P点的走法有792-300=492种。

这题其实可以用程序算出来 
简单的动态规划 
dp[i][j] = dp[i][j-1] + dp[i-1][j];

代码如下:

 #include <iostream>
 #include <cstdio>
 #include <algorithm>
 #include <string>

 using namespace std;
 int main()
 {

   int dp[][] = {};

   for(int i = ; i <= ; i++)
     for(int j = ; j <= ; j++)
         dp[i][j] = dp[i-][j] + dp[i][j-];

     int dp2[][] = {};
     dp2[][] = ;

     for(int i = ; i <= ; i++)
         for(int j = ; j <= ; j++)
             dp2[i][j] = dp2[i-][j] + dp2[i][j-];

     cout<<dp[][] - dp2[][] * dp[][]<<endl;

   return ;
 }

或者如下图：