NOIP 车站分级 (luogu 1983 & codevs 3294 & vijos 1851) - 拓扑排序 - bitset

描述

一条单向的铁路线上,依次有编号为 1, 2, ..., n 的 n 个火车站。每个火车站都有一个级别,最低为 1 级。现有若干趟车次在这条线路上行驶,每一趟都满足如下要求:如果这趟车次停靠了火车站 x,则始发站、终点站之间所有级别大于等于火车站 x 的都必须停靠。
(注意:起始站和终点站自然也算作事先已知需要停靠的站点)
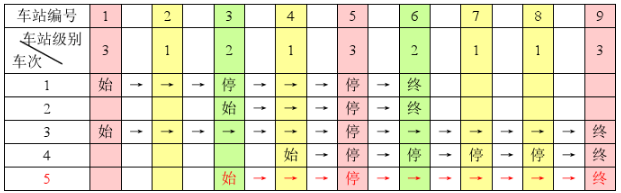
例如,下表是 5 趟车次的运行情况。其中,前 4 趟车次均满足要求,而第 5 趟车次由于停靠了 3 号火车站(2 级)却未停靠途经的 6 号火车站(亦为 2 级)而不满足要求。

现有 m 趟车次的运行情况(全部满足要求),试推算这 n 个火车站至少分为几个不同的级别。

格式

输入格式

第一行包含 2 个正整数 n, m,用一个空格隔开。
第 i + 1 行(1 ≤ i ≤ m)中,首先是一个正整数 s i (2 ≤ s i ≤ n),表示第 i 趟车次有 s i 个停靠站;接下来有 s i 个正整数,表示所有停靠站的编号,从小到大排列。每两个数之间用一个空格隔开。输入保证所有的车次都满足要求。

输出格式

输出只有一行,包含一个正整数,即 n 个火车站最少划分的级别数。

样例1

样例输入1

9 2
4 1 3 5 6
3 3 5 6

Copy

样例输出1

2

Copy

样例2

样例输入2

9 3
4 1 3 5 6
3 3 5 6
3 1 5 9

Copy

样例输出2

3

Copy

限制

每个测试点1s。

提示

对于 20%的数据,1 ≤ n, m ≤ 10;
对于 50%的数据,1 ≤ n, m ≤ 100;
对于 100%的数据,1 ≤ n, m ≤ 1000

来源

NOIP 2013 普及组

---

　　题目大意 (题目很简洁，不需(会)要(写)大意)

　　显然拓扑排序。(哪来那么多显然？)

　　这是一个拓扑排序比较基本的应用吧。

　　现在考虑如何建图，首先确定节点u连向节点v的一条有向边表示什么，表示v比u的等级高(严格大于)。

　　那么拓扑排序进行了多少层就是答案了。

　　因为从起点到终点间停靠的站的等级大于等于这两个站，所以不确定，不能连边，但是，中间没有停靠的站一定比这些停靠了的站等级低，故这中间所有没有停靠的站，向所有停靠了的站连1条有向边。

　　然而这样很遗憾的是，理论上O(n³)是会TLE，所以我们需要一些黑科技优化。(但实际上，普及组的数据比较水。。。所以可以过)

　　我们直接考虑点i会向哪些点连边。首先我们需要枚举所有航线，如果这个点在它的起点和终点间，并且没有停靠，我们就需要向这些停靠的点连边。这个实质上是将一些需要连边的顶点集合取并，所以考虑bitset黑科技优化，来代替暴力连边。

　　因此总时间复杂度成功降为。就算是ccf老年机卡一卡就过去了。

　　(这里不得不吐槽一下洛谷的评测鸡真的是ccf老年机标配，洛谷上跑bitset优化后的程序和在vijos和codevs上跑n³大暴力的时间差不多，不过记事本一遍A真地很开心，一个编译错误都没有)

Code

 /**
  * luogu
  * Problem#1983
  * Accepted
  * Time: 764ms
  * Memory: 12132k
  */
 #include <bits/stdc++.h>
 using namespace std;
 #define smax(a, b) a = max(a, b)

 int n, m;
 bitset<> *g;
 bitset<> *stop;
 int *ss, *st;

 inline void init() {
     scanf("%d%d", &n, &m);
     g = new bitset<>[(n + )];
     stop = new bitset<>[(m + )];
     ss = new int[(m + )];
     st = new int[(m + )];
     for(int i = , c, t; i <= m; i++) {
         scanf("%d%d", &c, &ss[i]);
         c -= ;
         stop[i][ss[i]] = ;
         while(c--) {
             scanf("%d", &t);
             stop[i][t] = ;
         }
         scanf("%d", st + i);
         stop[i][st[i]] = ;
     }
 }

 int *dag;
 int *dep;
 queue<int> que;
 inline void topu() {
     for(int i = ; i <= n; i++)
         if(!dag[i])
             que.push(i), dep[i] = ;

     while(!que.empty()) {
         int e = que.front();
         que.pop();
         for(int i = ; i <= n; i++) {
             if(!g[e][i])    continue;
             dag[i]--, smax(dep[i], dep[e] + );
             if(!dag[i])    que.push(i);
         }
     }
 }

 inline void solve() {
     dag = new int[(n + )];
     dep = new int[(n + )];
     memset(dag, , sizeof(int) * (n + ));
     memset(dep, , sizeof(int) * (n + ));
     for(int i = ; i <= n; i++) {
         for(int j = ; j <= m; j++)
             if(i >= ss[j] && i <= st[j] && !stop[j][i])
                 g[i] |= stop[j];
         for(int j = ; j <= n; j++)
             if(g[i][j])
                 dag[j]++;
     }
     topu();
     int res = ;
     for(int i = ; i <= n; i++)
         smax(res, dep[i]);
     printf("%d\n", res);
 }

 int main() {
     init();
     solve();
     return ;
 }