浅谈Trie树

Trie树，也叫字典树。顾名思义，它就是一个字典

字典是干什么的？查找单词！（英文字典哦）

个人认为字典树这个名字起得特别好，因为它真的跟字典特别像，一会r你就知道了。

注：trie的中文翻译就是单词查找树

一、引入

先来看一个题：

给你n个单词构成一个字典，再给你一个单词，问此单词在字典中有没有出现。

简单，暴力！

时间复杂度：n*单词长度

再来看一个题：

给你n个单词构成一个字典，再给你m个单词，问这m个单词在字典中有没有出现。

再暴力！

时间复杂度：n*单词长度+m*n*单词长度

n≤1e4，m≤1e4，单词长度≤1e3

boom！

(╯‵□′)╯︵┻━┻

所以，为什么要学习使用Trie树？

因为它快！

二、概念

我们首先来看看Trie树是啥

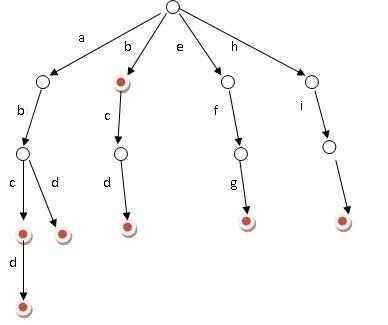
↑就是它

我们来解剖一下，好好研究研究（Trie树：瑟瑟发抖）

首先，我们发现树的每条边上都有一个字母

这就是Trie树的样子，每条边上都有一个字母，每个顶点代表从根到该节点的路径所对应的字符串（根结点除外）

其次，有些节点是红色的，有些则不是

这是什么意思呢？

结点不是代表单词嘛

所以如果结点标红，代表该单词在字典中实际出现过

如果看不太懂，不要紧，继续往下

三、插入单词（构建Trie树）

这里进入正题。第一步，构建trie树

就好比你想要查找单词，首先得有字典才行吧

step1：初始化

Trie树为空，只包含一个孤零零的根结点

step2：插入单词（注：这里假设所有单词仅由小写字母构成）

插入一个单词的步骤如下：

（1）对于Trie树，我们从根结点开始，设该节点为P；对于这个单词，我们从第一个字母开始，设此字符为s

（2）扫描P下方的所有边，看s有没有出现过

如果出现了，设s与P→Q这条边上的字符相同，则P=Q

如果没有出现，另建一条边，使该边上的字母为s，新节点为Q，然后P=Q

（3）s变为该单词的下一个字符，重复步骤2，直到扫描完整个单词为止

---

以概念中的那个图为例

首先我们要插入abc这个单词

（1）P为根结点，s为'a'

发现根结点下方无'a'，所以新建一条边

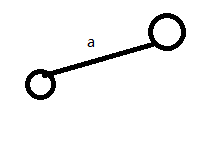
（2）P为a下方那个结点，s为'b'

发现P下方无'b'，所以新建一条边

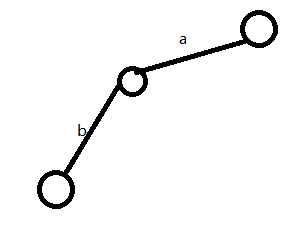
（3）P为b下方那个结点，s为'c'

发现P下方无'c'，所以新建一条边

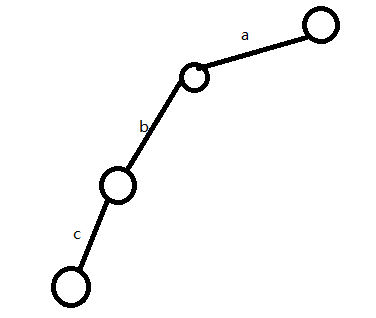
（4）发现abc这个单词插入完成，所以在当前的s做个标记，表示abc是一个出现过的单词

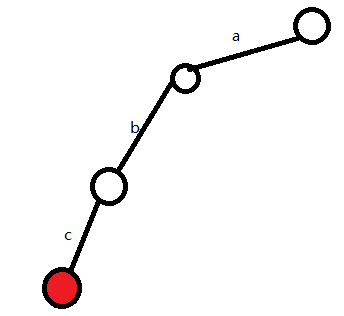
接着我们按照相同的步骤插入bcd、efg和hij

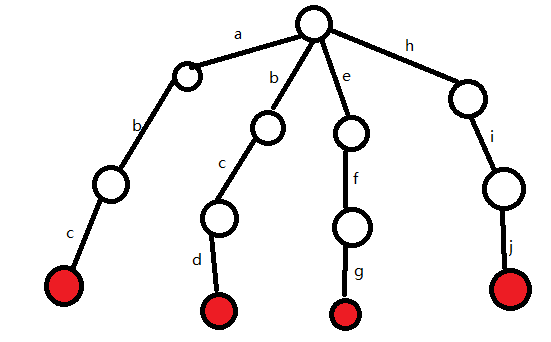
接下来插入abcd

（1）P为根结点，s为'a'

发现根结点下方有'a'，所以P变为'a'下方的结点

（2）P为a下方那个结点，s为'b'

发现P下方有'b'，所以P变为'b'下方的结点

（3）P为b下方那个结点，s为'c'

发现P下方有'c'，所以P变为'c'下方的结点

（4）P为c下方那个红色的结点，s为'd'

发现P下方无'd'，所以所以新建一条边

（5）单词abcd插入完毕，将当前的s做标记

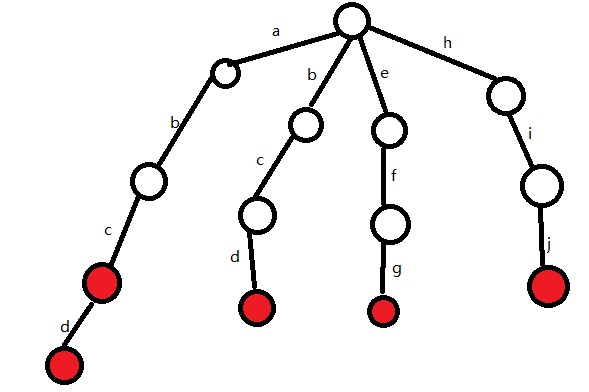
下面按照相同的方法，继续插入单词abd和b

插入完成后Trie树如下：

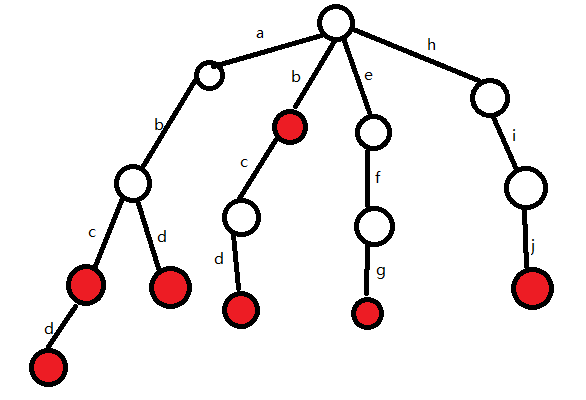
看看一样不：

(右下那条边应该是j）

我们可以发现，在Trie树中有相同前缀的单词共用相同的前缀，这样就可以大大的优化空间和时间

插入单词的时间复杂度为O(NE)（N为单词个数，E为单词长度）

参考代码：

void insert(char *s)//s为要插入的字符串
{
    int len=strlen(s);
    int u=;//1为根节点
    for(int i=;i<len;i++)
    {
        int c=s[i]-'a';//'a'有时需换成'A'或'0'
        if(!trie[u][c])//没有共同前缀，建立一个新的
            ch[u][c]=++tot;//tot为总点数
        u=ch[u][c];//继续向下插入单词
    }
    book[u]=true;//标记是一个出现过的单词（图中涂红色）
}

insert

四、查找单词

词典有了，接下来就可以查词了

在trie树中查单词就跟查字典一样。先查首字母，然后第二个，第三个……

查找过程跟插入的过程很像：

（1）对于Trie树，我们从根结点开始，设该节点为P；对于这个单词，我们从第一个字母开始，设此字符为s

（2）扫描P下方的所有边，看s有没有出现过

如果出现了，设s与P→Q这条边上的字符相同，则P=Q

如果没有出现，则该单词没有出现过，直接返回false

（3）s变为该单词的下一个字符，重复步骤2，直到扫描完整个单词为止

（4）扫描完成后，判断节点P有没有被标记（是不是某个出现过的单词的结尾）。如果标记了，那么该单词出现过，返回true；如果没有标记，那么该单词是词典中这个单词的前缀，返回false。

对于（4）讲解一下：

还是这棵Trie树：

我们查找ef这个单词：

（1）P为根结点，s为'e'

发现根结点下方有'e'，所以P变为'e'下方的结点

（2）P为e下方那个结点，s为'f'

发现P下方有'f'，所以P变为'f'下方的结点

（3）查找完成，发现P这里没有标记，所以ef是词典中单词efg的前缀，而不是直接出现在了词典里，返回false

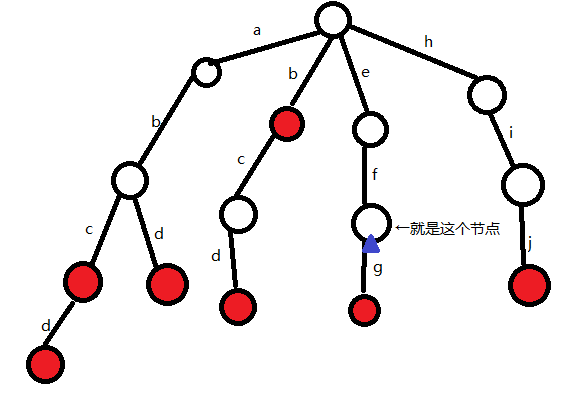
再举一个例子，我们查找abd这个单词：

（1）P为根结点，s为'a'

发现根结点下方有'a'，所以P变为'a'下方的结点

（2）P为a下方那个结点，s为'b'

发现P下方有'b'，所以P变为'b'下方的结点

（3）P为b下方那个结点，s为'd'

发现P下方有'd'，所以P变为'd'下方的结点

（3）查找完成，发现P这里有标记，所以abd是词典中的单词，返回true

应该讲的挺明白的

查找的一个单词的时间复杂度O(E)，比起暴力的O(NE)要快多了

参考代码：

bool find(char *s)//s为要查找的字符串
{
    int len=strlen(s);
    int u=;//1为根节点
    for(int i=;i<len;i++)
    {
        int c=s[i]-'a';//'a'有时需换成'A'或'0'
        if(!trie[u][c])//单词没有出现，直接返回false
            return false;
        u=ch[u][c];//继续向下查找单词
    }
    //如果扫描完了这个单词
    return true;//是某个单词的前缀
}

查找单词是否是词典中某单词的前缀

bool find(char *s)//s为要查找的字符串
{
    int len=strlen(s);
    int u=;//1为根节点
    for(int i=;i<len;i++)
    {
        int c=s[i]-'a';//'a'有时需换成'A'或'0'
        if(!trie[u][c])//单词没有出现，直接返回false
            return false;
        u=ch[u][c];//继续向下查找单词
    }
    //如果扫描完了这个单词
    return book[u];//如果出现过，返回true；如果没有出现过（是前缀），返回false
}

查找单词是否在词典中出现过

模板题：

https://www.cnblogs.com/llllllpppppp/p/9366344.html

本文部分图片来源于网络

部分内容参考《信息学奥赛一本通.提高篇》第二部分第三章 Trie字典树

若需转载，请注明https://www.cnblogs.com/llllllpppppp/p/9449846.html

~祝大家编程顺利~