查找->动态查找表->平衡二叉树

文字描述

平衡二叉树(Balanced Binary Tree或Height-Balanced Tree)

　　因为是俄罗斯数学家G.M.Adel’son-Vel’skii和E.M.Landis在1962年提出来的，所以又称AVL树。它或者是一颗空树，或者是具有下列性质的二叉树：它的左子树和右子树都是平衡二叉树，且左子树和右子树的深度之差的绝对值不超过1。若将二叉树上结点的平衡因子BF(Balanced Factor)定义为该结点的左子树的深度减去它的右子树的深度，则平衡二叉树上所有结点的平衡因子只可能是-1，0和1。只要二叉树上有一个结点的平衡因子的绝对值大于1，则该二叉树就是不平衡的。

　　那么如何使二叉排序树成为平衡树呢？即在一颗二叉排序树中因插入一个结点后失去平衡的话，怎么调整才能使之重新平衡呢？

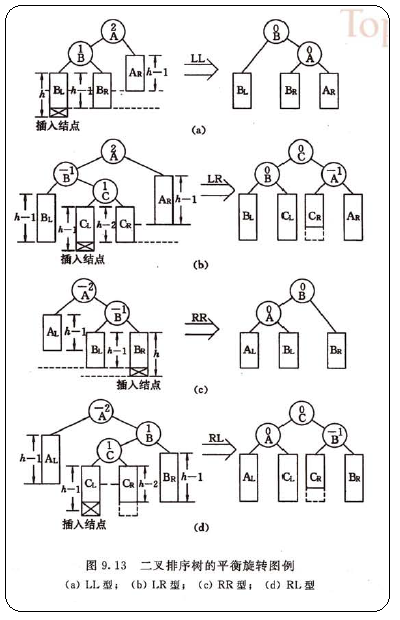
　　一般情况下，假设由于在二叉排序树上插入结点而失去平衡的最小子树根结点的指针a(即a是离插入结点最近，且平衡因子绝对值超过1的祖先结点)，则失去平衡后进行调整的规律可归纳为下面4中情况：

　　(1)单向右旋平衡处理，图9.13(a)所示：在*a的左子树根结点的左子树上插入结点后，*a的平衡因子由1增至2，致使以*a为根的子树失去平衡，则需进行一次向右的顺时针旋转操作。

　　(2)双向旋转(先左后右)，图9.13(b)所示：在*a的左子树根结点的右子树上插入结点后，*a的平衡因子由1增至2，致使以*a为根的子树失去平衡，则需进行两次旋转(先左旋后右旋)操作。

　　(3)单向左旋平衡处理，图9.13(c)所示：在*a的右子树根结点的右子树上插入结点后，*a的平衡因子由-1变为-2，致使以*a为根的子树失去平衡，则需进行一次向左的逆时针旋转操作。

　　(4)双向旋转(先右后左)，图9.13(d)所示：在*a的右子树根结点的左子树上插入结点后，*a的平衡因子由-1变为-2，致使以*a为根的子树失去平衡，则需进行两次选择(先右旋后左旋)

上诉4种情况中，(1)和(3)对称，(2)和(4)对称。它们旋转后依然能保持二叉排序树的特性且由不平衡变为平衡。可以用二叉排序树的特性(”对于二叉排序树，中序遍历所得关键字序列自小至大有序”)证明之。

示意图

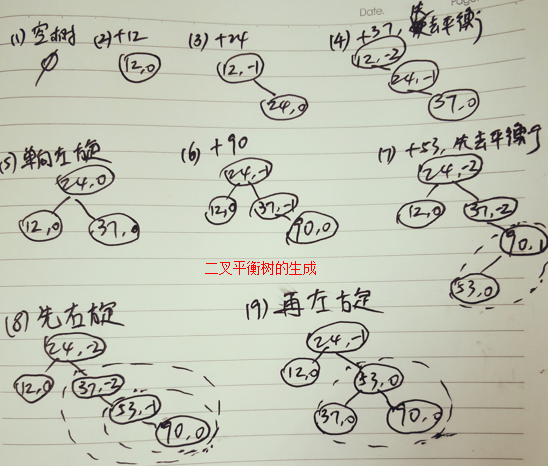
算法分析

　　在平衡二叉排序树上查找的时间复杂度为logn， 不会出现最差的情况。

代码实现

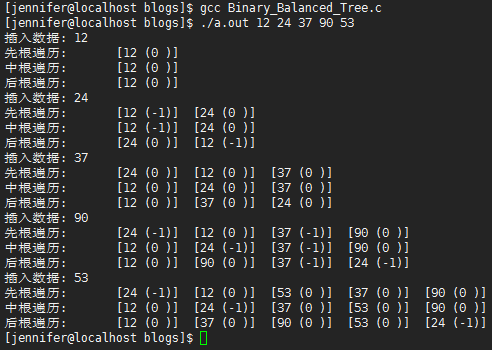
 //./a.out 45 12 53 3 37 100 24 61 90 78
 //./a.out 45 12 53 100 61
 //测试
 #include <stdio.h>
 #include <stdlib.h>
 #include <string.h>

 #define DEBUG
 #define TRUE     1
 #define FALSE    0
 #define LH        +1    //左高
 #define EH        0    //等高
 #define RH        -1    //右高
 #define EQ(a,b)    ((a)==(b))
 #define LT(a,b)    ((a)< (b))
 #define LQ(a,b)    ((a)<=(b))
 #define LCHILD 1
 #define RCHILD 2

 typedef int ElemType;
 typedef int Boolean;
 //平衡二叉树采用二叉链表作为存储结构
 typedef struct BSTNode{
     ElemType data;
     //结点的平衡因子
     int bf;
     //左,右孩子指针
     struct BSTNode *lchild, *rchild;
 }BSTNode, *BSTree; 

 /*右旋平衡处理算法
  *
  *对以*p为根的二叉排序树作右旋处理，处理之后p指向新的树根结点，即旋转之前的左子树的根结点。f始终指向*p的父亲结点
  *提示：建议结合图9.13(a)看，此处*p, lc相当于图中A、B结点。
  */
 void R_Rotate(BSTree *p, BSTree f){
     //*p是其父亲结点f的左孩子结点还是右孩子结点？
     int flag = -;
     if(f && (f->lchild == (*p))){
         //*p是f的左孩子结点
         flag = LCHILD;
     }
     if(f && (f->rchild == (*p))){
         //*p是f的右孩子结点
         flag = RCHILD;
     }

     //lc指向*p的左子树根结点
     BSTNode *lc = (BSTNode*)(*p)->lchild;
     //lc的右子树挂接为*p的左子树
     (*p)->lchild = lc->rchild;
     //p指向新的根结点
     lc->rchild = *p;
     *p = lc;

     //更新父亲结点f的孩子结点指针
     if(f && (flag==LCHILD)){
         f->lchild = *p;
     }
     if(f && (flag==RCHILD)){
         f->rchild = *p;
     }
 }

 /*左旋平衡处理算法
  *
  *提示：和右旋平衡算法是对称的，建议结合图9.13(c)看，此处*p,rc相当图图中的A、B结点。
  */
 void L_Rotate(BSTree *p, BSTree f){
     int flag = -;
     if(f && (f->lchild == (*p))){
         flag = LCHILD;
     }
     if(f && (f->rchild == (*p))){
         flag = RCHILD;
     }

     BSTNode *rc = (BSTNode*)(*p)->rchild;
     (*p)->rchild = rc->lchild;
     rc->lchild = *p;
     *p = rc;

     if(f && (flag==LCHILD)){
         f->lchild = *p;
     }
     if(f && (flag==RCHILD)){
         f->rchild = *p;
     }
 }

 //对指针T所指结点为根的二叉树作左平衡选择处理，本算法结束时，指针T指向新的根结点，f为*T的父亲结点。
 void LeftBalance(BSTree *T, BSTree f){
     //lc指向*T的左子树根结点
     BSTNode *lc = (BSTNode*)(*T)->lchild;
     BSTNode *rd;
     //检查*T的左子树的平衡度，并作相应平衡处理
     switch(lc->bf){
         //新结点插在了*T的左孩子的左子树上，要做单右旋处理
         case LH:
             lc->bf = (*T)->bf = EH;
             R_Rotate(T, f);
             break;
         //新结点插在了*T的左孩子的右子树上，要做双旋处理
         case RH:
             //rd指向*T的左孩子的右子树根
             rd = lc->rchild;
             switch(rd->bf){
                 //修改*T及其左孩子的平衡因子。
                 //提示：建议结合图9.13(b)看，此处*T, lc, rd相当于图中A、B、C结点。
                 case LH:
                     (*T)->bf = RH;
                     lc->bf = EH;
                     break;
                 case EH:
                     (*T)->bf = EH;
                     lc->bf = EH;
                     break;
                 case RH:
                     (*T)->bf = EH;
                     lc->bf = LH;
                     break;
             }
             rd->bf = EH;
             //对*T的左子树lc做左旋平衡处理
             L_Rotate(&lc, *T);
             //对*T左右旋平衡处理
             R_Rotate(T, f);
             break;
         default:
             break;
     }
     return ;
 }

 //和左平衡算法是对称的，此处不再赘述
 void RightBalance(BSTree *T, BSTree f){
     BSTNode *rc = (BSTNode*)(*T)->rchild;
     BSTNode *ld;
     switch(rc->bf){
         case LH:
             //提示：建议结合图9.13(d)看，此处*T, rc, ld相当于图中的A、B、C结点。
             ld = rc->lchild;
             switch(ld->bf){
                 case LH:
                     (*T)->bf = EH;
                     rc->bf = RH;
                     break;
                 case EH:
                     (*T)->bf = EH;
                     rc->bf = EH;
                     break;
                 case RH:
                     (*T)->bf = LH;
                     rc->bf = EH;
                     break;
             }
             ld->bf = EH;
             R_Rotate(&rc, *T);
             L_Rotate(T, f);
             break;
         case RH:
             rc->bf = (*T)->bf = EH;
             L_Rotate(T, f);
             break;
         default:
             break;
     }
     return ;
 }

 /*平衡二叉树的插入算法
  *
  *若在平衡二叉排序树中T不存在和e有相同关键字的结点，则插入一个数据元素为e
  *的新结点点，并返回TRUE；否则返回FALSE。若因插入而使二叉排序树失去平衡，则
  *作平衡选择处理，布尔变量taller反映T长高与否。
  */
 int InsertAVL(BSTree *T,BSTree f, ElemType e, Boolean *taller){
     if(!(*T)){
         //插入新结点，树"长高"，置taller为TRUE，并返回TRUE
         (*T) = (BSTree)malloc(sizeof(BSTNode));
         (*T)->data = e;
         (*T)->bf = EH;
         (*T)->lchild = (*T)->rchild = NULL;
         *taller = TRUE;
         return TRUE;
     }else{
         if(EQ((*T)->data, e)){
             //树中已经存在和e相同的结点，不再插入，并返回FALSE
             *taller = FALSE;
             return FALSE;
         }
         if(LT(e, (*T)->data)){
             //应该继续在*T的左子树上进行搜索
             BSTree *p = malloc(sizeof(BSTree));
             *p = (BSTree)((*T)->lchild);
             if(!InsertAVL(p, *T, e, taller)){
                 //未插入
                 free(p);
                 return FALSE;
             }
             //已插入到*T的左子树中, 更新*T的左子树结点
             (*T)->lchild = *p;
             if(*taller){
                 //左子树"长高"，检查*T的平衡度
                 switch((*T)->bf){
                     case LH:
                         //原本左子树比右子树高，现在左子树上又长高了，需要作左平衡处理
                         LeftBalance(T, f);
                         (*T)->bf = EH;
                         *taller = FALSE;
                         break;
                     case EH:
                         //原本左子树和右子树等高，现在左子树上又长高了，现在*T的左子树比右子树高
                         (*T)->bf = LH;
                         *taller = TRUE;
                         break;
                     case RH:
                         //原本左子树和右子树矮，现在左子树上又长高了，现在*T的左子树比右子树等高
                         (*T)->bf = EH;
                         *taller = FALSE;
                         break;
                 }
             }
             free(p);
             return TRUE;
         }else{
             //应该继续在*T的右子树上进行搜索
             BSTree *p2 = malloc(sizeof(BSTree));
             *p2= (BSTree)((*T)->rchild);
             if(!InsertAVL(p2, *T, e, taller)){
                 //未插入
                 free(p2);
                 return FALSE;
             }
             //已插入到*T的右子树中, 更新*T的右子树结点
             (*T)->rchild = *p2;
             if(*taller){
                 //右子树"长高"，检查*T的平衡度
                 switch((*T)->bf){
                     case LH:
                         //原本左子树比右子树高，现在右子树上长高了，现在*T的左子树比右子树等高
                         (*T)->bf = EH;
                         *taller = FALSE;
                         break;
                     case EH:
                         //原本左子树和右子树等高，现在右子树上长高了，现在*T的左子树比右子树矮
                         (*T)->bf = RH;
                         *taller = TRUE;
                         break;
                     case RH:
                         //原本左子树和右子树矮，现在右子树上长高了，需要作右平衡处理
                         RightBalance(T, f);
                         (*T)->bf = EH;
                         *taller = FALSE;
                         break;
                 }
             }
             free(p2);
             return TRUE;
         }
     }
 }
 //二叉树先根遍历算法的函数声明
 int PreOrderTraverse(BSTree T);
 //二叉树中根遍历算法的函数声明
 int InOrderTraverse(BSTree T);
 //二叉树后根遍历算法的函数声明
 int PostOrderTraverse(BSTree T);
 //分别以先、中、后根遍历算法依次打印二叉树中的结点元素的函数声明
 void print(BSTree T);

 int main(int argc, char *argv[])
 {
     if(argc < )
         return FALSE;
     int i = ;
     ElemType e;
     Boolean taller;
     BSTree Tree = NULL;
     for(i=; i<argc; i++){
         e = atoi(argv[i]);
         printf("插入数据: %d\n", e);
         InsertAVL(&Tree, NULL, e, &taller);
         print(Tree);

     }
     return TRUE;
 }

 //分别以先、中、后根遍历算法依次打印二叉树中的结点元素的函数实现
 void print(BSTree T){
     printf("先根遍历:\t");
     PreOrderTraverse(T);
     printf("\n");    

     printf("中根遍历:\t");
     InOrderTraverse(T);
     printf("\n");    

     printf("后根遍历:\t");
     PostOrderTraverse(T);
     printf("\n");
 }

 //二叉树先根遍历算法的函数实现
 int PreOrderTraverse(BSTree T){
     if(T){
         printf("[%-3d(%-2d)]  ", ((BSTNode*)T)->data, ((BSTNode*)T)->bf);
         PreOrderTraverse((BSTree)T->lchild);
         PreOrderTraverse((BSTree)T->rchild);
     }
     return ;
 }

 //二叉树中根遍历算法的函数实现
 int InOrderTraverse(BSTree T){
     if(T){
         InOrderTraverse((BSTree)T->lchild);
         printf("[%-3d(%-2d)]  ", ((BSTNode*)T)->data, ((BSTNode*)T)->bf);
         InOrderTraverse((BSTree)T->rchild);
     }
     return ;
 }

 //二叉树后根遍历算法的函数实现
 int PostOrderTraverse(BSTree T){
     if(T){
         PostOrderTraverse((BSTree)T->lchild);
         PostOrderTraverse((BSTree)T->rchild);
         printf("[%-3d(%-2d)]  ", ((BSTNode*)T)->data, ((BSTNode*)T)->bf);
     }
     return ;
 }

平衡二叉树

运行