论文笔记：GREEDY FUNCTION APPROXIMATION: A GRADIENT BOOSTING MACHINE

Boost是集成学习方法中的代表思想之一，核心的思想是不断的迭代。boost通常采用改变训练数据的概率分布，针对不同的训练数据分布调用弱学习算法学习一组弱分类器。在多次迭代的过程中，当前次迭代所用的训练数据的概率分布会依据上一次迭代的结果而调整。也就是说训练数据的各样本是有权重的，这个权重本身也会随着迭代而调整。Adaboost(后面补一篇介绍这个的文章吧)在迭代的过程中通过不断调整数据分布的权重来达到提高性能的目的，GBM(Gradient Boosting Machine)则是在迭代的过程中，新的模型建立在之间建立模型损失函数的梯度下降方向上，为什么这么做是有效的，数学语言是最严谨的，让我们从数学的角度出发理解一下。

　　从数值优化的角度入手。对于加性模型$F(X|\Theta) $，我们通过优化$\Theta$得到模型的最优解

$$ \theta^* = \mathop{\arg\min}_{\theta} \ \mathrm{L} (\theta).$$

其中，$\mathrm{L}(\theta) = E_(y,x)\mathrm{L}(y,F(X|\Theta))$　，那么对于$F(X|\Theta) $其最优解为$F^*(x) =F(x|\Theta^*) $　。由于$F(X|\Theta) $是个加性模型，通常有$P^* = \sum_{i = 0}^m p_i$。在优化P的过程中，对于迭代的第m步骤，我们以前获得了m-1个模型，在计算第m个模型的时候，我们要对前m-1个模型的集成求梯度，$g_m$为求得的梯度如下所示$$g_m=\{g_{jm}\} = \{{\big[\frac{\partial{\phi(P)}}{\partial{P_j}}\big]_{p = p_{(m-1)}}}\}$$其中$$P_{m-1} = \sum_{i=0}^{m-1} P_i$$求出梯度之后，我们更新$$p_m = -\rho_mg_m$$其中，$$\rho_m = \mathop{\arg\min}_\rho\ L(P_{m-1}-\rho{g_m})$$

简单整理一下，对于加性模型$F(X|\Theta) $，我们通过对损失函数$L(\theta)$求得$\theta$沿着最优解下降的方向$g_m$，为了确定下降的步长，也就是$\rho$,我们构造一个关于$P_{m-1}+p_m$的损失函数，其中$p_m = -\rho{g_m}$。确定了梯度$g_m$以及在该梯度下的步长$\rho$，$p_m$也就求解出来了。

　　上述的推导过程中，建立在训练的数据集是连续无穷的情况下，对于有限的数据集合在计算$g_m$的过程中，求出的最优解$F^*(X)$对应的点不一定是我们训练集中的点。简单来说就是对于前m-1个模型计算出来的梯度对于有限的训练数据集，并不能直接作为新的基学习器的梯度方向。为了解决这个问题，论文预先假设一个先验分布$h(x_i;a)$,通过最小化损失函数的方式让$h(x_i;a)$逼近预先计算好的梯度$g_m$，论文中用的损失函数是MSE,过程如下所示$$a_m=\mathop{\arg\min}_{a,\beta} \sum_{i=1}^N[{-g_m(x_i)-\beta{h(x_i;a)}}]^2 $$

整体的GBM算法流程如下所示

第三步对应的便是求前m-1个模型的梯度， 第四步根据球出来的梯度通过最小化损失函数的方法让基模型（h(x;a)）逼近梯度下降的方向，第五步也是通过最小化集成的函数预测结果与label的损失也确定第k个基模型的权重。

紧扣最小化似然函数这个过程就不难理解这么做的缘由了。

2019.9.7 在实际理解GBM的调参过程中发现对CART如何学习以及

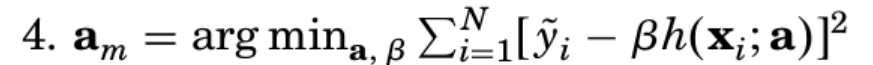
如何影响CART的参数的学习并没有理解清楚.
首先要弄清楚CART学习的参数究竟是什么,这里指的是最优分裂属性以及分裂属性值的选择,外界的干预通过label影响最优划分属性的选择,具体的介绍见:https://blog.csdn.net/niuniuyuh/article/details/76922210