图的深度优先搜索(DFS)和广度优先搜索(BFS)算法

深度优先（DFS）

深度优先遍历，从初始访问结点出发，我们知道初始访问结点可能有多个邻接结点，深度优先遍历的策略就是首先访问第一个邻接结点，然后再以这个被访问的邻接结点作为初始结点，访问它的第一个邻接结点。总结起来可以这样说：每次都在访问完当前结点后首先访问当前结点的第一个邻接结点。

我们从这里可以看到，这样的访问策略是优先往纵向挖掘深入，而不是对一个结点的所有邻接结点进行横向访问。

算法大概过程：

1.把整个图的结构用矩阵来表示，如图：

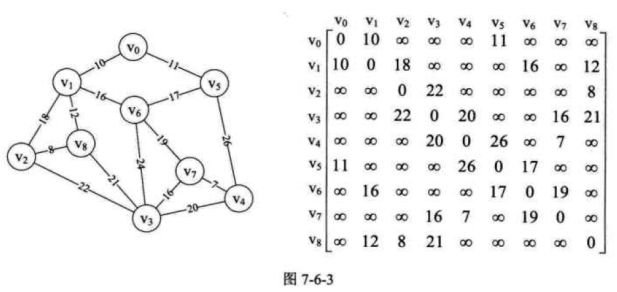
2.我们从第一个顶点（v0）开始遍历，拿到第一个邻接点（二维矩阵里是v1），这个时候我们再对v1进行遍历，v0已经被访问过了所以选择跳过，这时再拿到v2，对v2开始进行遍历。。。以此类推！

代码实现如下：

// 获取某顶点的第一个邻接点
	private int getFirstNeighbor(int index) {
		for (int i = 0; i < vertexSize; i++) {
			if (matrix[index][i] > 0 && matrix[index][i] < MAX_WEIGHT) {
				// 找到了第一邻接点
				return i;
			}
		}
		return -1;
	}

	// 根据前一个邻接点下标，来取得下一个邻接点
	/**
	 * @param v1
	 *            表示要找的顶点
	 * @param index
	 *            表示该顶点相对于哪个邻接点去获取下一个邻接点
	 * @return
	 */
	private int getNextNeighbor(int v1, int index) {
		for (int i = index + 1; i < vertexSize; i++) {
			if (matrix[v1][i] > 0 && matrix[v1][i] < MAX_WEIGHT) {
				return i;
			}
		}
		return -1;
	}

	private void depthSearch(int i) {
		isVisited[i] = true;// 证明当前顶点被访问过了
		// 获取当前顶点的邻接点
		int w = getFirstNeighbor(i);
		// 只要w不是-1
		while (w != -1) {
			// 证明i确实有邻接点
			// 判断w是否被访问过
			if (!isVisited[w]) {
				// 如果没有被访问过,就继续深度遍历w顶点
				System.out.println("深度优先访问到的顶点：" + w);
				depthSearch(w);
			}
			// 如果当前邻接点被访问过了，就继续搜索除了这个w外其他的点
			w = getNextNeighbor(i, w);
		}
	}

	public void depthFirstSearch() {
		// 这是对外提供
		isVisited = new boolean[vertexSize];
		for (int i = 0; i < vertexSize; i++) {
			if (!isVisited[i]) {
				System.out.println("深度优先访问到的顶点：" + i);
				depthSearch(i);
			}
		}
		// 遍历完后，记得把布尔数组归为
		isVisited = new boolean[vertexSize];
	}

　　

广度优先（BFS）

广度优先搜索类似于我们的二叉树的层次遍历，我们还是以v0作为起始点，根据二维矩阵，我们找到v0的第一个邻接点，之后再找到v0的第二个邻接点，直到找不到v0的邻接点为止，由图可知，v0就俩邻接点v1，v5。遍历完后，继续遍历v1的邻接点，v1的遍历完后，开始遍历v5的。。。以此类推！

代码如下：

// 广度优先遍历算法
	public void broadFirstSearch() {
		isVisited = new boolean[vertexSize];
		for (int i = 0; i < vertexSize; i++) {
			if (!isVisited[i]) {
				System.out.println("广度优先访问到的顶点：" + i);
				broadSearch(i);
			}
		}
		isVisited = new boolean[vertexSize];
	}

	private void broadSearch(int i) {
		// 类似于二叉树的层次遍历
		int u, w;
		LinkedList<Integer> queue = new LinkedList<>();
		isVisited[i] = true;
		queue.add(i);
		while (!queue.isEmpty()) {
			u = queue.removeFirst();// 顶点
			w = getFirstNeighbor(u);
			while (w != -1) {
				if (!isVisited[w]) {
					System.out.println("广度优先访问到的顶点：" + w);
					isVisited[w] = true;
					queue.add(w);
				}
				// 拿到后面的邻接点
				w = getNextNeighbor(u, w);
			}
		}
	}