两种非常常见的非线性单元：rectified linear units (ReLUs) 和 leaky ReLUs

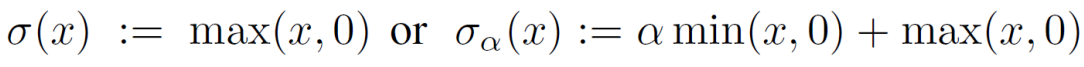
我们选取binary hinge loss进行二分类

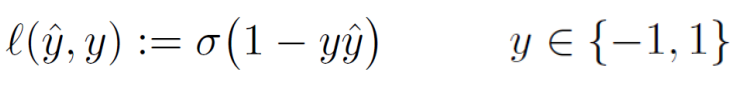
对于多分类，我们可以定义multiclass hinge loss

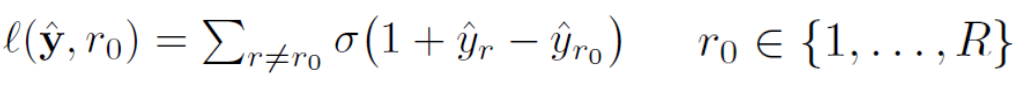
定义Ω为网络的参数空间， L(ω)为loss。

由于我们选了ReLU非线性单元作为loss, 那么L(ω)是分片线性的。对于参数空间，我们可以将其进行一个划分，

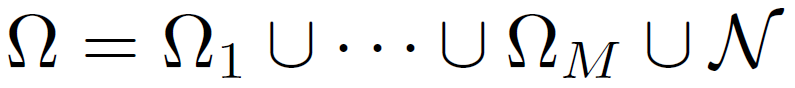
分成有限个open cells Ωu 和 边界N，则损失函数L(ω)在cell的内部是光滑的，在边界上是不可微的。

下面我们将loss限制在某个cell  Ωu上单独考虑，并且loss拥有multilinear form. 由于multilinear form是调和的，由strong maximum principle知，极值点必定在边界处N. 换句话说，ReLU 神经网络 with hinge loss L(ω)是不存在可微的局部极值点的。

目前为止，我们可以知道局部极值有两种情况，

Type I (Flat). 局部极值在cell中，loss为常值。

Type II (Sharp). 局部极值在边界N上。

Main Result 1.   在Type II局部极值点，L(ω)>0.

也就是说，如果存在极值0，那么Type II极值点都是sub-optimal的。

若我们考虑更一般的情况：fully connected networks with leaky ReLU nonlinearities. 那么我们有以下结果，

Main Result 2.  在Type I局部极值点，L(ω)=0. 在Type II局部极值点，L(ω)>0.

在存在极值0的情况下，flat 局部极小值都是optimal的，sharp 局部极小值都是sub-optimal的。若不存在极值0，所有的局部极值点都是sharp的。

未完待续。。。

The Multilinear Structure of ReLU Networks的更多相关文章

  1. 课程一(Neural Networks and Deep Learning)，第四周（Deep Neural Networks） —— 3.Programming Assignments: Deep Neural Network - Application

    Deep Neural Network - Application Congratulations! Welcome to the fourth programming exercise of the ...

  2. DEEP LEARNING WITH STRUCTURE

    DEEP LEARNING WITH STRUCTURE Charlie Tang is a PhD student in the Machine Learning group at the Univ ...

  3. 课程一(Neural Networks and Deep Learning)总结——2、Deep Neural Networks

    Deep L-layer neural network 1 - General methodology As usual you will follow the Deep Learning metho ...

  4. 深度学习材料：从感知机到深度网络A Deep Learning Tutorial: From Perceptrons to Deep Networks

    In recent years, there’s been a resurgence in the field of Artificial Intelligence. It’s spread beyo ...

  5. [综述]Deep Compression/Acceleration深度压缩/加速/量化

    Survey Recent Advances in Efficient Computation of Deep Convolutional Neural Networks, [arxiv '18] A ...

  6. 网络压缩论文集(network compression)

    Convolutional Neural Networks ImageNet Models Architecture Design Activation Functions Visualization ...

  7. CVPR 2017 Paper list

    CVPR2017 paper list Machine Learning 1 Spotlight 1-1A Exclusivity-Consistency Regularized Multi-View ...

  8. (转) Deep Reinforcement Learning: Playing a Racing Game

    Byte Tank Posts Archive Deep Reinforcement Learning: Playing a Racing Game OCT 6TH, 2016 Agent playi ...

  9. 社区发现算法问题&&NetworkX&&Gephi

    在做东西的时候用到了社区发现,因此了解了一下有关社区发现的一些问题 1,社区发现算法 (1)SCAN:一种基于密度的社团发现算法 Paper: <SCAN: A Structural Clust ...

随机推荐

  1. JavaScript DOM 编程艺术(第二版) 初读学习笔记

    这本书留给我的印象就是结构.表现和行为层的分离,以及书后面部分一直在强调的最佳实践原则:平稳退化,逐步增强,向后兼容以及性能考虑. 要注意这不是一本JavaScript入门书籍~ 2.1 准备工作 用 ...

  2. cef加载flash的办法

    cef有2种加载flash插件的方式, 1,npapi,这种方式是调用系统自带的flash插件,由于有安全性方面的问题,已经被新版cef禁用. 2,ppapi,也就是 pepper flash,这是谷 ...

  3. 数据库中TOP—N查询

    1)查询1-4的数据 SELECT rownum, sno, cno, score FROM (SELECT * FROM sc order by score desc) WHERE rownum & ...

  4. Vue实现点击时间获取时间段查询功能

    二话不说,先上图 实现如上代码: //获取本周第一天 showWeekFirstDay: function () { let Nowdate = new Date(); let WeekFirstDa ...

  5. 应用安全 - 工具 | 平台 - gitlist - 漏洞 - 汇总

    简介 用途 Github仓库查看器 CVE-2014-4511 Date 类型 远程代码执行 影响范围 gitlist 0.4.0及之前版本

  6. USACO4.4 Frame Up【拓扑排序】

    题意居然还读了好久... 读完题目之后大概就知道拓扑排序了.用拓扑可以求出一些字母之间的关系,谁先,谁后.但是这个关系不是唯一确定的,所以就会产生多种方案(题目还要求按字典序输出所有的方案) 输出方案 ...

  7. PHP Excel导入

    public function importFile() { $file = request()->file('file'); $params = $this->request->p ...

  8. c++ | final

    C++11的关键字final有两个用途:(1).禁止虚函数被重写:(2).禁止基类被继承. 在派生类中,可以同时使用overried和final.

  9. MySQL数据类型 约束

    一.数据库CDGS. 库 增   create database 库名; 删   drop 库名; 改 alter database 库名称 修改的属性名称; 查 show databases;#查看 ...

  10. 注入(Injection)

    注入(Injection)是: Java EE提供了注入机制,使您的对象能够获取对资源和其他依赖项的引用,而无需直接实例化它们.通过使用将字段标记为注入点的注释之一来装饰字段或方法,可以在类中声明所需 ...