支持向量机(Support Vector Machine)-----SVM之SMO算法(转)
此文转自两篇博文 有修改
序列最小优化算法(英语:Sequential minimal optimization, SMO)是一种用于解决支持向量机训练过程中所产生优化问题的算法。SMO由微软研究院的约翰·普莱特(John Platt)发明于1998年,目前被广泛使用于SVM的训练过程中,并在通行的SVM库libsvm中得到实现。
1998年,SMO算法发表在SVM研究领域内引起了轰动,因为先前可用的SVM训练方法必须使用复杂的方法,并需要昂贵的第三方二次规划工具。而SMO算法较好地避免了这一问题。
前面最后留下来一个对偶函数最后的优化问题,原式为:
-----------------这个是由拉格朗日方法 然后求偏导 列式带入核函数得到的目标函数
SMO就是要解这个凸二次规划问题,这里的C是个很重要的参数,它从本质上说是用来折中经验风险和置信风险的,C越大,置信风险越大,经验风险越小;并且所有的因子都被限制在了以C为边长的大盒子里。
算法详述
(1)、 KKT条件
SMO是以C-SVC的KKT条件为基础进行后续操作的,这个KKT条件是:
其中
上述条件其实就是KT互补条件,SVM学习——软间隔优化一文,有如下结论:
从上面式子可以得到的信息是:当时,松弛变量
,此时有:
,对应样本点就是误分点;当
时,松弛变量
为零,此时有
,对应样本点就是内部点,即分类正确而又远离最大间隔分类超平面的那些样本点;而
时,松弛变量
为零,有
,对应样本点就是支持向量。
(2)、凸优化问题停止条件
对于凸优化问题,在实现时总需要适当的停止条件来结束优化过程,停止条件可以是:
1、监视目标函数的增长率,在它低于某个容忍值时停止训练,这个条件是最直白和简单的,但是效果不好;
2、监视原问题的KKT条件,对于凸优化来说它们是收敛的充要条件,但是由于KKT条件本身是比较苛刻的,所以也需要设定一个容忍值,即所有样本在容忍值范围内满足KKT条件则认为训练可以结束;
3、监视可行间隙,它是原始目标函数值和对偶目标函数值的间隙,对于凸二次优化来说这个间隙是零,以一阶范数软间隔为例:
原始目标函数与对偶目标函数
的差为:
定义比率:
,可以利用这个比率达到某个容忍值作为停止条件。
(3)、SMO思想
沿袭分解思想,固定“Chunking工作集”的大小为2,每次迭代只优化两个点的最小子集且可直接获得解析解,算法流程:
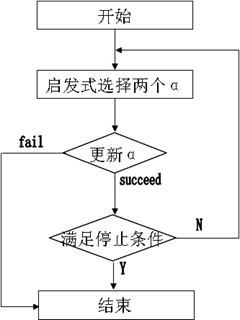
(4)、仅含两个Langrange乘子解析解
为了描述方便定义如下符号:
于是目标函数就变成了:
注意第一个约束条件:,可以将
看作常数,有
(
为常数,我们不关心它的值),等式两边同时乘以
,得到
(
为常数,其值为
,我们不关心它,
 )。将
)。将用上式替换则得到一个只含有变量
的求极值问题:
这下问题就简单了,对求偏导数得到:
将、
带入上式有:
带入、
,用
,表示误差项(可以想象,即使分类正确,
的值也可能很大)、
(
是原始空间向特征空间的映射),这里
可以看成是一个度量两个样本相似性的距离,换句话说,一旦选择核函数则意味着你已经定义了输入空间中元素的相似性。
最后得到迭代式:
注意第二个约束条件——那个强大的盒子:,这意味着
也必须落入这个盒子中,综合考虑两个约束条件,下图更直观:
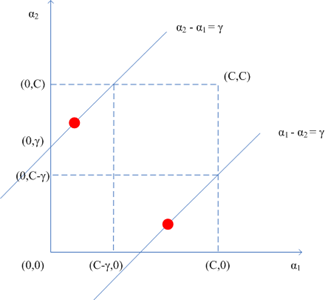
和
异号的情形
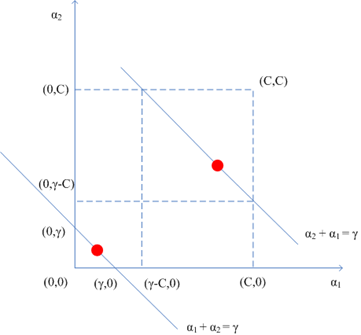
和
同号的情形
可以看到两个乘子既要位于边长为C的盒子里又要在相应直线上,于是对于
的界来说,有如下情况:
整理得下式:
又因为,
,消去
后得到:
(5).综上可总结出SMO的算法框架
SMO算法是一个迭代优化算法。在每一个迭代步骤中,算法首先选取两个待更新的向量,此后分别计算它们的误差项,并根据上述结果计算出 和
和 。最后再根据SVM的定义计算出偏移量
。最后再根据SVM的定义计算出偏移量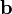 。对于误差项而言,可以根据
。对于误差项而言,可以根据 、
、 和b的增量进行调整,而无需每次重新计算。具体的算法如下:
和b的增量进行调整,而无需每次重新计算。具体的算法如下:
1. 随机数初始化向量权重 ,并计算偏移b。(这一步初始化向量权重只要使
,并计算偏移b。(这一步初始化向量权重只要使 符合上述的约束条件即可,原博文的程序就是range函数)
符合上述的约束条件即可,原博文的程序就是range函数)
2.初始化误差项 ,其中
,其中
3.选取两个向量作为需要调整的点(例如第一次下标为1,2两点,第二次下标3,4...........),然后
令其中
(
是原始空间向特征空间的映射),
4.if  >H 令
>H 令 =H if
=H if  <L 令
<L 令 =L (L,H前面已给出)
=L (L,H前面已给出)
5.令
6.利用更新的 和
和 修改
修改 和b的值
和b的值
7.如果达到终止条件,则算法停止,否则转向3
算法补充说明:
优化向量选择方法
可以采用启发式的方法选择每次迭代中需要优化的向量。第一个向量可以选取不满足支持向量机KKT条件的向量,亦即不满足
-
-

- 即:
-
其中
-
的向量。而第二个向量可以选择使得 最大的向量。
最大的向量。
终止条件
SMO算法的终止条件可以为KKT条件对所有向量均满足,或者目标函数 增长率小于某个阈值,即
增长率小于某个阈值,即
-
-
 (根据前面的凸优化问题停止条件所说,此效果可能不佳,可选择其他方法,见(2))
(根据前面的凸优化问题停止条件所说,此效果可能不佳,可选择其他方法,见(2))
-
---------------------------------以下内容是有关可行间隙方法,乘子优化,SMO加速问题,是深化的内容------------------------------------------------
(6)、启发式的选择方法
根据选择的停止条件可以确定怎么样选择点能对算法收敛贡献最大,例如使用监视可行间隙的方法,一个最直白的选择就是首先优化那些最违反KKT条件的点,所谓违反KKT条件是指:
其中KKT条件
由前面的停止条件3可知,对可行间隙贡献最大的点是那些
其中,
取值大的点,这些点导致可行间隙变大,因此应该首先优化它们(原因见原博文:http://www.cnblogs.com/vivounicorn/archive/2011/06/01/2067496.html)
SMO的启发式选择有两个策略:
启发式选择1:
最外层循环,首先,在所有样本中选择违反KKT条件的一个乘子作为最外层循环,用“启发式选择2”选择另外一个乘子并进行这两个乘子的优化,接着,从所有非边界样本中选择违反KKT条件的一个乘子作为最外层循环,用“启发式选择2”选择另外一个乘子并进行这两个乘子的优化(之所以选择非边界样本是为了提高找到违反KKT条件的点的机会),最后,如果上述非边界样本中没有违反KKT条件的样本,则再从整个样本中去找,直到所有样本中没有需要改变的乘子或者满足其它停止条件为止。
启发式选择2:
内层循环的选择标准可以从下式看出:
要加快第二个乘子的迭代速度,就要使最大,而在
上没什么文章可做,于是只能使
最大。
确定第二个乘子方法:
1、首先在非界乘子中寻找使得最大的样本;
2、如果1中没找到则从随机位置查找非界乘子样本;
3、如果2中也没找到,则从随机位置查找整个样本(包含界上和非界乘子)。
(7)、关于两乘子优化的说明
由式子
可知:
于是对于这个单变量二次函数而言,如果其二阶导数,则二次函数开口向下,可以用上述迭代的方法更新乘子,如果
,则目标函数只能在边界上取得极值(此时二次函数开口向上),换句话说,SMO要能处理
取任何值的情况,于是在
时有以下式子:
1、时:
2、时:
3、


分别将乘子带入得到两种情况下的目标函数值: 和
。显然,哪种情况下目标函数值最大,则乘子就往哪儿移动,如果目标函数的差在某个指定精度范围内,说明优化没有进展。
另外发现,每一步迭代都需要计算输出进而得到
,于是还要更新阈值
,使得新的乘子
、
满足KKT条件,考虑
、
至少有一个在界内,则需要满足
,于是
的迭代可以这样得到:
1、设在界内,则:
又因为:
于是有:
等式两边同乘后移项得:
;
2、设在界内,则:
;
3、设、
都在界内,则:情况1和情况2的
值相等,任取一个;
4、设、
都不在界内,则:
取值为情况1和情况2之间的任意值。
(8)、提高SMO的速度
从实现上来说,对于标准的SMO能提高速度的地方有:
1、能用缓存的地方尽量用,例如,缓存核矩阵,减少重复计算,但是增加了空间复杂度;
2、如果SVM的核为线性核时候,可直接更新,毕竟每次计算
的代价较高,于是可以利用旧的乘子信息来更新
,具体如下:
,应用到这个性质的例子可以参见SVM学习——Coordinate Desent Method。
3、关注可以并行的点,用并行方法来改进,例如可以使用MPI,将样本分为若干份,在查找最大的乘子时可以现在各个节点先找到局部最大点,然后再从中找到全局最大点;又如停止条件是监视对偶间隙,那么可以考虑在每个节点上计算出局部可行间隙,最后在master节点上将局部可行间隙累加得到全局可行间隙。
支持向量机(Support Vector Machine)-----SVM之SMO算法(转)的更多相关文章
- Support Vector Machine(4):SMO算法
经过上一篇的推导,我们的优化问题已经化为了如下等价形式: 我们在不考虑任何约束条件的情况下去想这个minimize的问题,可以将其抽象为: SMO算法的思想是,每次迭代,只改变一个参数,而将n-1个参 ...
- 支持向量机 support vector machine
SVM(support Vector machine) (1) SVM(Support Vector Machine)是从瓦普尼克(Vapnik)的统计学习理论发展而来的,主要针对小样本数据进行学习. ...
- 【机器学习实战】第6章 支持向量机(Support Vector Machine / SVM)
第6章 支持向量机 <script type="text/javascript" src="http://cdn.mathjax.org/mathjax/lates ...
- 故事描述SVM----支持向量机/support vector machine (SVM)
作者:简之链接:https://www.zhihu.com/question/21094489/answer/86273196来源:知乎著作权归作者所有.商业转载请联系作者获得授权,非商业转载请注明出 ...
- 机器学习经典算法笔记-Support Vector Machine SVM
可供使用现成工具:Matlab SVM工具箱.LibSVM.SciKit Learn based on python 一 问题原型 解决模式识别领域中的数据分类问题,属于有监督学习算法的一种. 如图所 ...
- 支持向量机(Support Vector Machine,SVM)
SVM: 1. 线性与非线性 核函数: 2. 与神经网络关系 置信区间结构: 3. 训练方法: 4.SVM light,LS-SVM: 5. VC维 u-SVC 与 c-SVC 区别? 除参数不同外, ...
- 第八篇:支持向量机 (Support Vector Machine)
前言 本文讲解如何使用R语言中e1071包中的SVM函数进行分类操作,并以一个关于鸢尾花分类的实例演示具体分类步骤. 分析总体流程 1. 载入并了解数据集:2. 对数据集进行训练并生成模型:3. 在此 ...
- SVM之SMO算法(转)
支持向量机(Support Vector Machine)-----SVM之SMO算法(转) 此文转自两篇博文 有修改 序列最小优化算法(英语:Sequential minimal optimizat ...
- 支持向量机SVM(Support Vector Machine)
支持向量机(Support Vector Machine)是一种监督式的机器学习方法(supervised machine learning),一般用于二类问题(binary classificati ...
随机推荐
- Java笔记—— 格式化的输入和输出
精确输出 可以用8个字符的宽度和小数点后了两个字符的精度打印x. double x = 10000.0 /3.0; System.out.printf("%8.2f\n",x);/ ...
- java 多线程Callable和Runable执行顺序问题详解
详见:http://blog.yemou.net/article/query/info/tytfjhfascvhzxcyt125 毫无疑问 Runnable会进行异步执行,此处不多说,主要说明Call ...
- 启动springjar
java -jar cms-exporter-0.0.1-SNAPSHOT.jar --spring.config.location=classpath:./config
- !JS实战之随机像素图
JavaScript实例分享之----画随机像素图.随机像素图(作者自己取得名字)指的是一张图片上每一个像素的颜色都是随机的.此时应该能联想到这幅图多么眼花缭乱,好吧,我们用JS来实现它的原因是JS很 ...
- 软件工程(GZSD2015)学生博客列表
2015年贵州师范大学软件工程课程学生博客列表 陈小丽 郑倩 唐洁 周娟 李利思 肖俊 罗文豪 周静 徐明艳 毛涛 邓洪虹 岳庆 李盼 安坤 何亚 涂江凤 张义平 杨明颢 杨家堂 胡贵玲 寿克霞 吴明 ...
- 201521123104 《Java程序设计》第6周学习总结
1. 本周学习总结 1.1 面向对象学习暂告一段落,请使用思维导图,以封装.继承.多态为核心概念画一张思维导图,对面向对象思想进行一个总结. 2. 书面作业 1. clone方法 1.1 Object ...
- java命令行执行带依赖jar包的main函数
有时候客户端没有运行环境,需要将程序放到服务器上执行,可按如下操作: 1.创建libs文件夹,将运行过程中依赖的jar包全部拷贝到此处; 2.编译.执行 javac -Djava.ext.dirs=l ...
- Hibernate第十二篇【二级缓存介绍、缓存策略、查询缓存、集合缓存】
Hibernate二级缓存介绍 前面我们已经讲解过了一级缓存,一级缓存也就是Session缓存,只在Session的范围内有效-作用时间就在Session的作用域中,范围比较小 Hibernate为我 ...
- 06jQuery-05-事件
不同的浏览器绑定事件的代码都不太一样,所以我们使用jQuery来写代码的话,可以屏蔽不同浏览器之间的差异. 在jQuery中,可以使用 on 来绑定一个事件,指定事件的名称和对应的处理函数: // 获 ...
- SQL基础巩固
1.一定要记住,SQL 对大小写不敏感! 2.分号是在数据库系统中分隔每条 SQL 语句的标准方法,这样就可以在对服务器的相同请求中执行一条以上的语句. 如果您使用的是 MS Access 和 SQL ...
