【2016北京集训测试赛（八）】 crash的数列 （思考题）

Description

---

题解

　　题目说这是一个具有神奇特性的数列！这句话是非常有用的因为我们发现，如果套着这个数列的定义再从原数列引出一个新数列，它居然还是一样的......

　　于是我们就想到了能不能用多点数列套着来加速转移呢？

　　但是发现好像太多数列套起来是可以烦死人的......

　　我们就采用嵌套两次吧（第三次以后规律就不明显了），记原数列为A，第一层嵌套为B，第二层嵌套为C。

　　

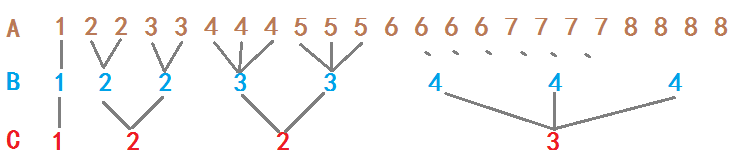
　　我们其实可以发现一些规律，对于Ci，它对应了B中i的个数；对于Bi，它对应了A中i的个数。

　　稍加处理即可，我们一边计算一边模拟数列的运算，同时可以计算实际上在A中前进的步数，如果超过了n就暴力模拟退格。

　　时间复杂度？？？极快

　　PS: 原先写了一个很慢的预处理程序，本地正常编译，对拍没问题；结果上去给OJ的O2卡了我的 用常数做上限的数组的循环到上限的语句gg。（其实还是被空间限制卡掉了1个点......）

 #include <cstdio>
 using namespace std;
 typedef long long ll;
 const int N=;
 ll n,sum,id,end,lis[N];
 int main(){
     scanf("%lld",&n);
     lis[]=lis[]=;
     end=id=sum=;
     for(int i=;;i++)
         for(int j=;j<=lis[i];j++){
             lis[++end]=i;
             sum+=end*i;
             id+=i;
             if(sum<n) continue;
             while(sum-end>=n)
                 id--,sum-=end;
             printf("%lld\n",id);
             return ;
         }
     return ;
 }

奇妙代码

　　注意处理一些细节，比如初始各变量的值（lis[2]=1实际上是为了顺利进入循环而已）。

---