PTA (Advanced Level) 1014 Waiting in Line

Waiting in Line

　　Suppose a bank has N windows open for service. There is a yellow line in front of the windows which devides the waiting area into two parts. The rules for the customers to wait in line are:

• The space inside the yellow line in front of each window is enough to contain a line with Mcustomers. Hence when all the N lines are full, all the customers after (and including) the (st one will have to wait in a line behind the yellow line.
• Each customer will choose the shortest line to wait in when crossing the yellow line. If there are two or more lines with the same length, the customer will always choose the window with the smallest number.
• Customer​i​​ will take T​i​​ minutes to have his/her transaction processed.
• The first N customers are assumed to be served at 8:00am.

　　Now given the processing time of each customer, you are supposed to tell the exact time at which a customer has his/her business done.

　　For example, suppose that a bank has 2 windows and each window may have 2 custmers waiting inside the yellow line. There are 5 customers waiting with transactions taking 1, 2, 6, 4 and 3 minutes, respectively. At 08:00 in the morning, customer​1​​ is served at window​1​​ while customer​2​​ is served at window​2​​. Customer​3​​ will wait in front of window​1​​ and customer​4​​ will wait in front of window​2​​. Customer​5​​ will wait behind the yellow line.

　　At 08:01, customer​1​​ is done and customer​5​​ enters the line in front of window​1​​ since that line seems shorter now. Customer​2​​ will leave at 08:02, customer​4​​ at 08:06, customer​3​​ at 08:07, and finally customer​5​​ at 08:10.

Input Specification:

　　Each input file contains one test case. Each case starts with a line containing 4 positive integers: N (≤, number of windows), M (≤, the maximum capacity of each line inside the yellow line), K (≤, number of customers), and Q (≤, number of customer queries).

　　The next line contains K positive integers, which are the processing time of the K customers.

　　The last line contains Q positive integers, which represent the customers who are asking about the time they can have their transactions done. The customers are numbered from 1 to K.

Output Specification:

　　For each of the Q customers, print in one line the time at which his/her transaction is finished, in the format HH:MM where HH is in [08, 17] and MM is in [00, 59]. Note that since the bank is closed everyday after 17:00, for those customers who cannot be served before 17:00, you must output Sorry instead.

Sample Input:

2 2 7 5
1 2 6 4 3 534 2
3 4 5 6 7

Sample Output:

08:07
08:06
08:10
17:00
Sorry

解题思路：
　　本题意思是银行有n个窗口，每个窗口前最多可以排m个人，现在有k个人，所有窗口从8点开始服务，到17点停止接受服务，不过如果17点前接受了服务，无论多晚也会服务完该客户。要求按查询输出客户完成服务的时间（愚蠢的顾客们只要选定一个排队的窗口就会一直排到关门，即使其他窗口空了也不换）。

　　本题每组测试数据首先给出4个整数，分别为窗口数量n、最大排队人数m、客户人数k、查询数量q，之后一行包括k个整数，代表服务每个客户所需要的时间（分钟），下一行包括q个整数，代表查询的客户。

　　首先分析一下样例

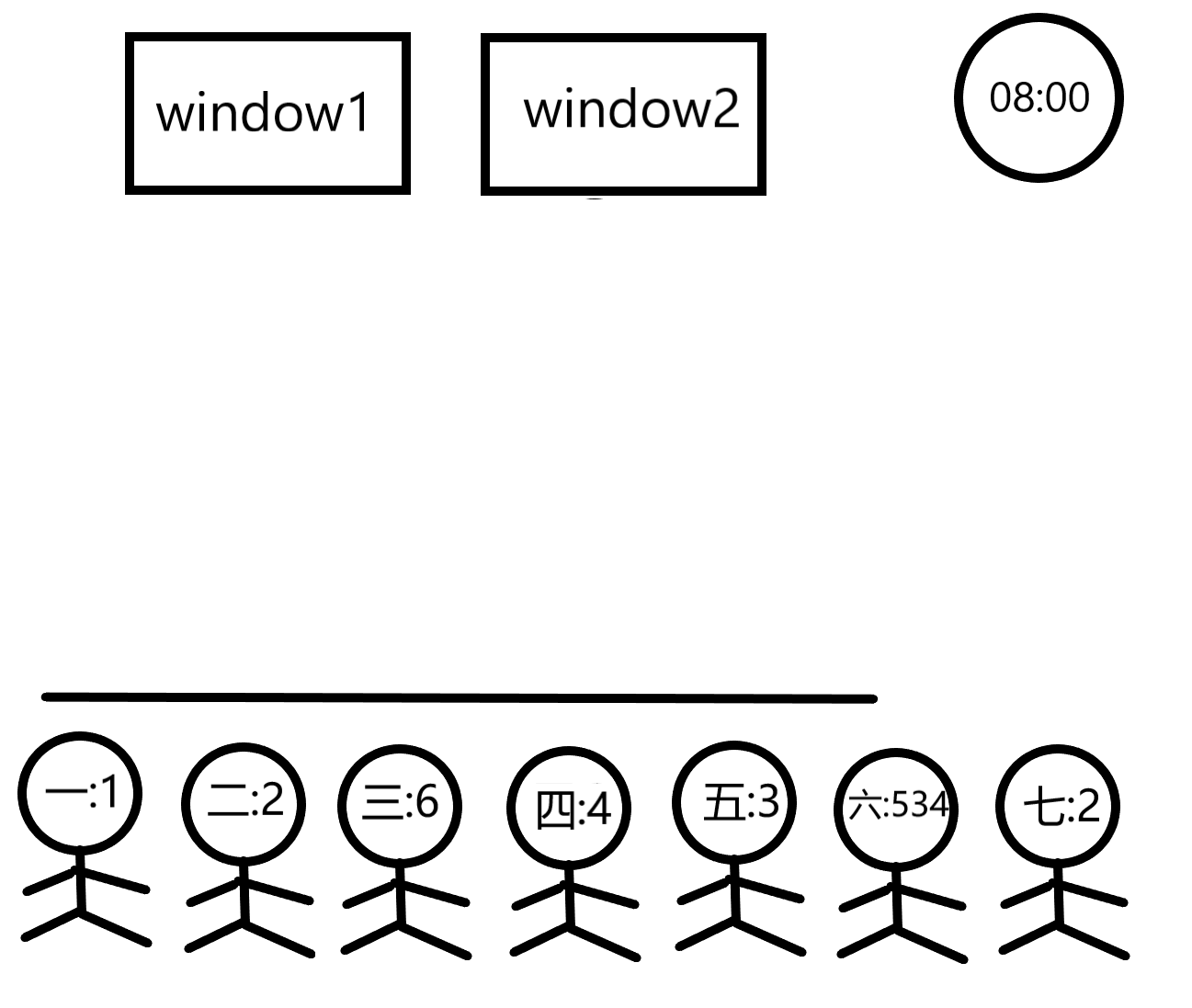
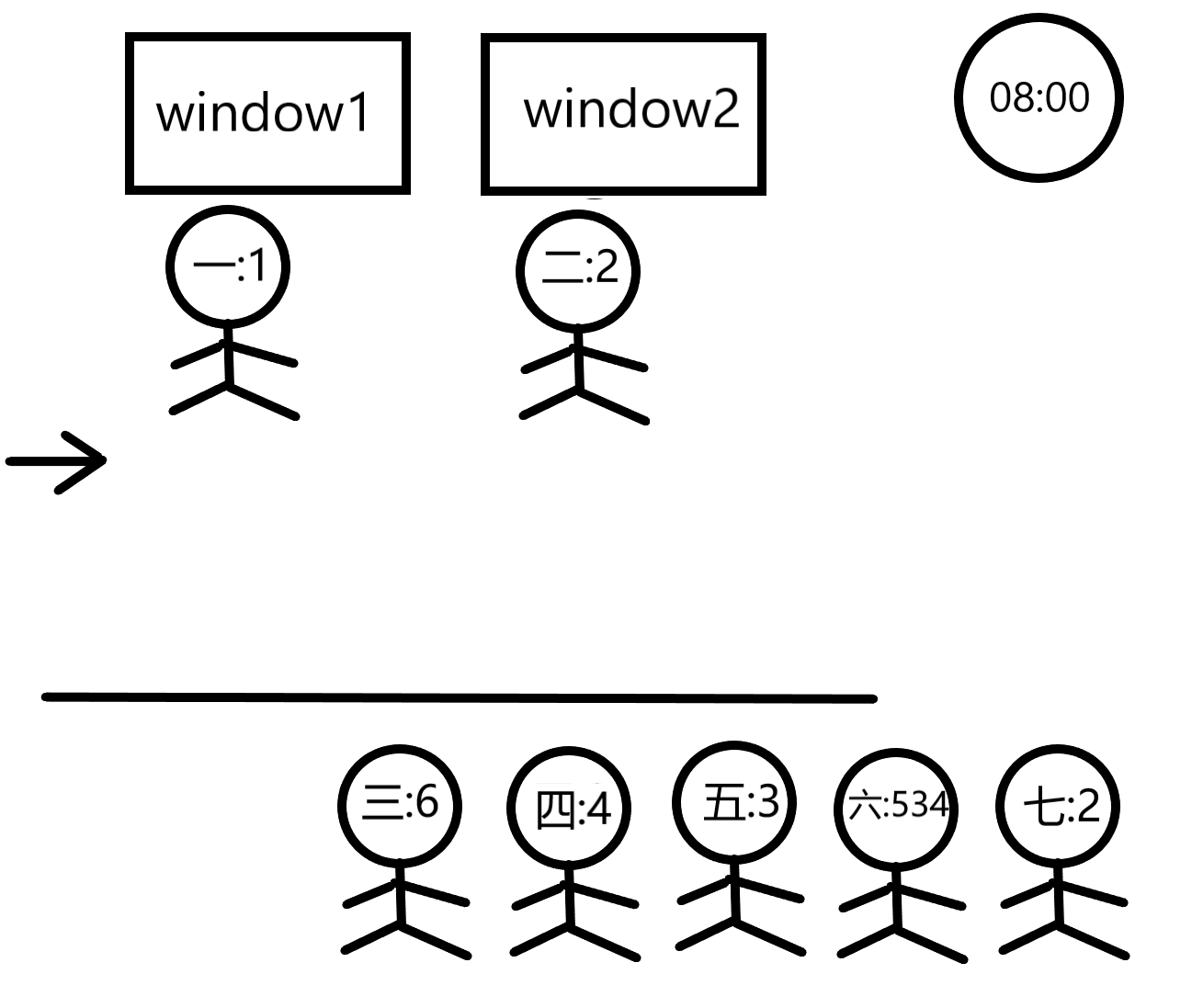
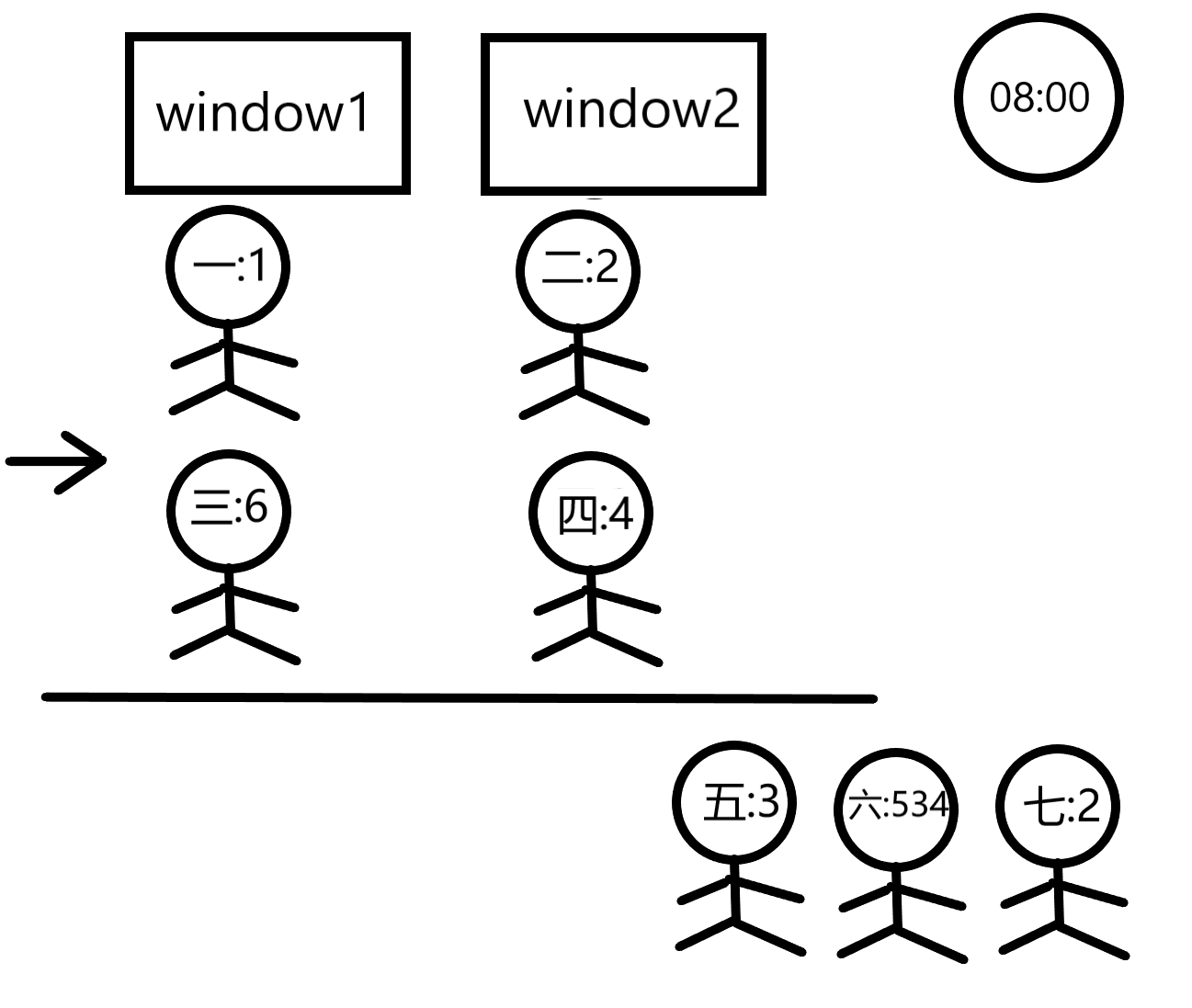
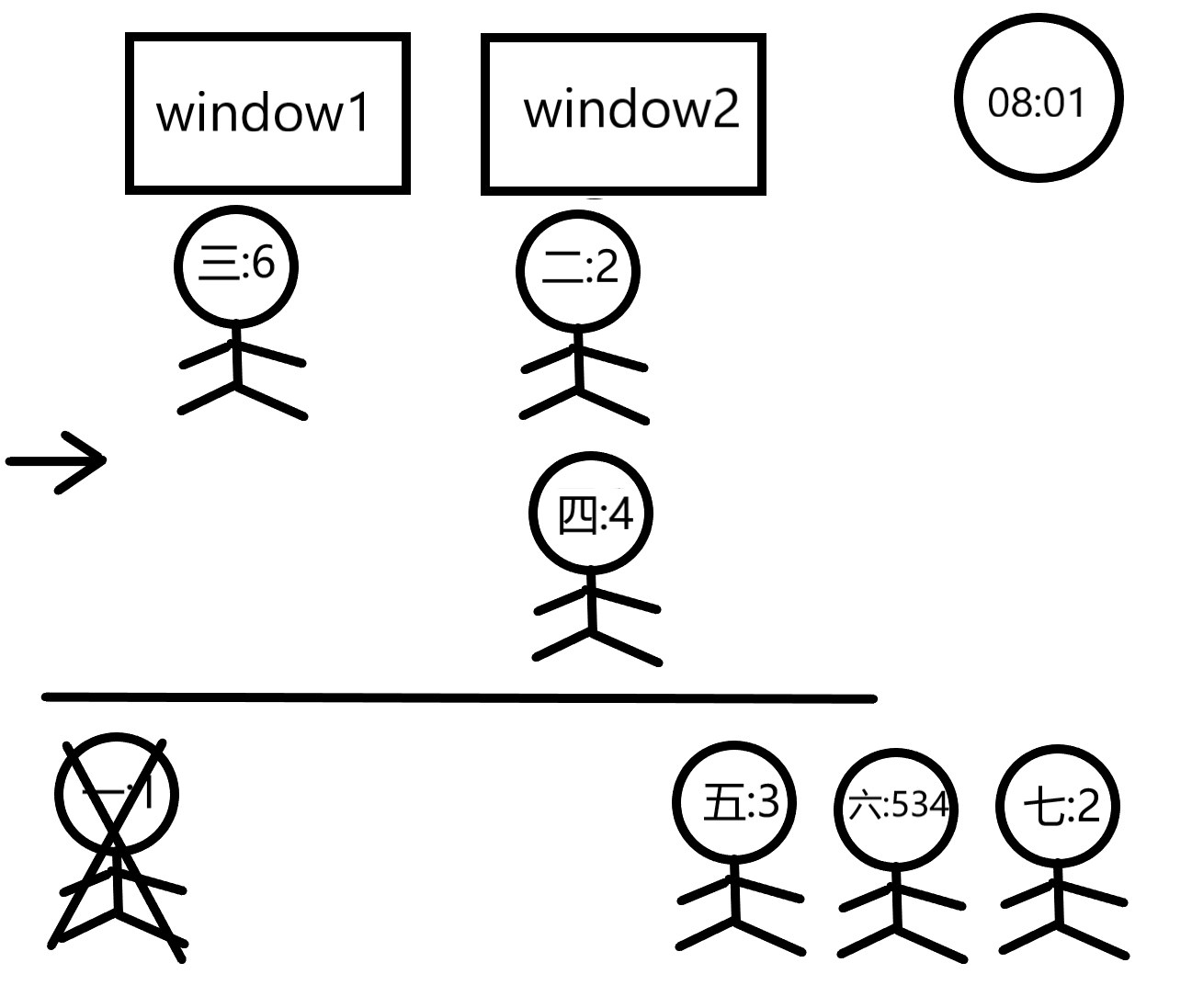
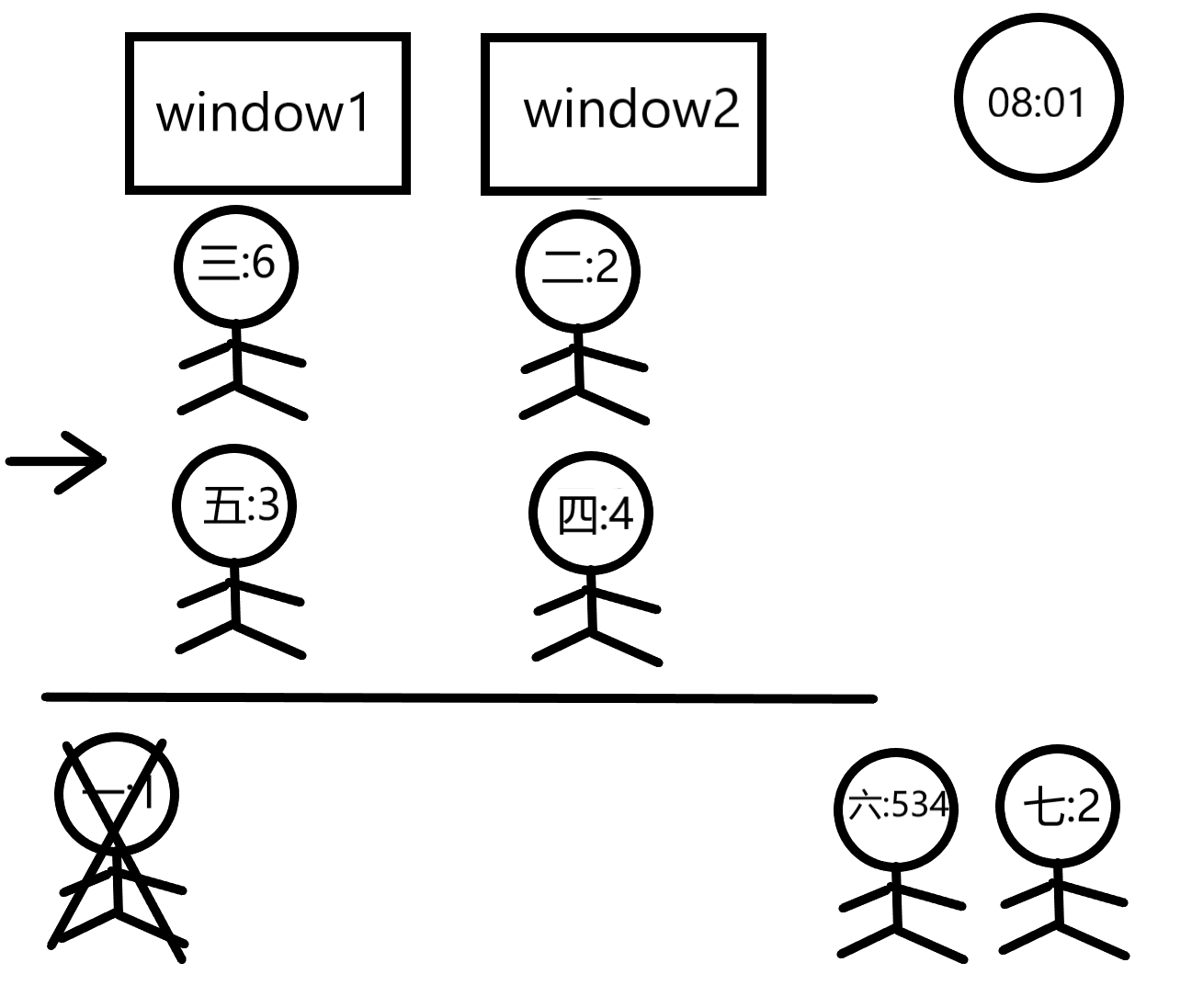
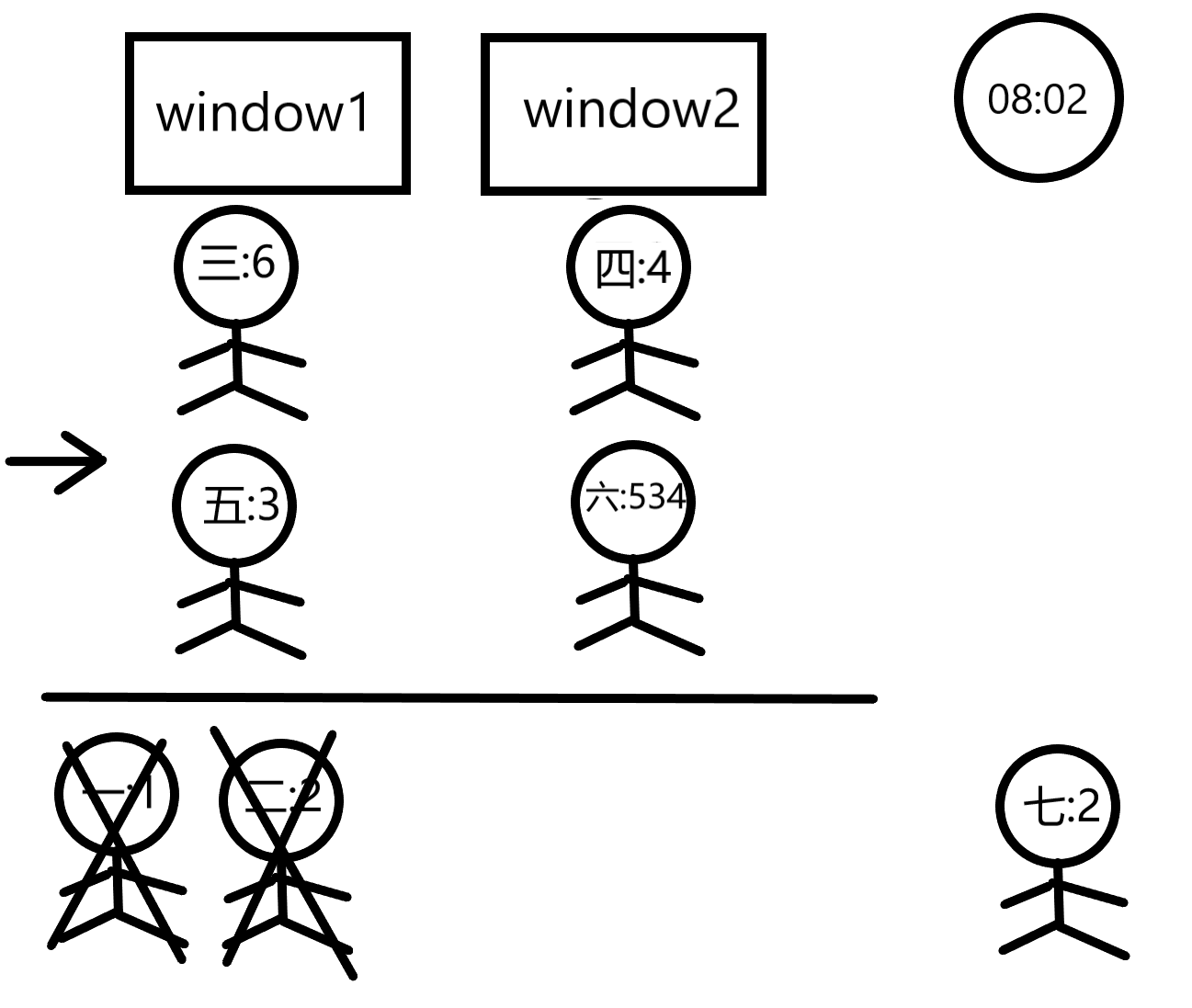
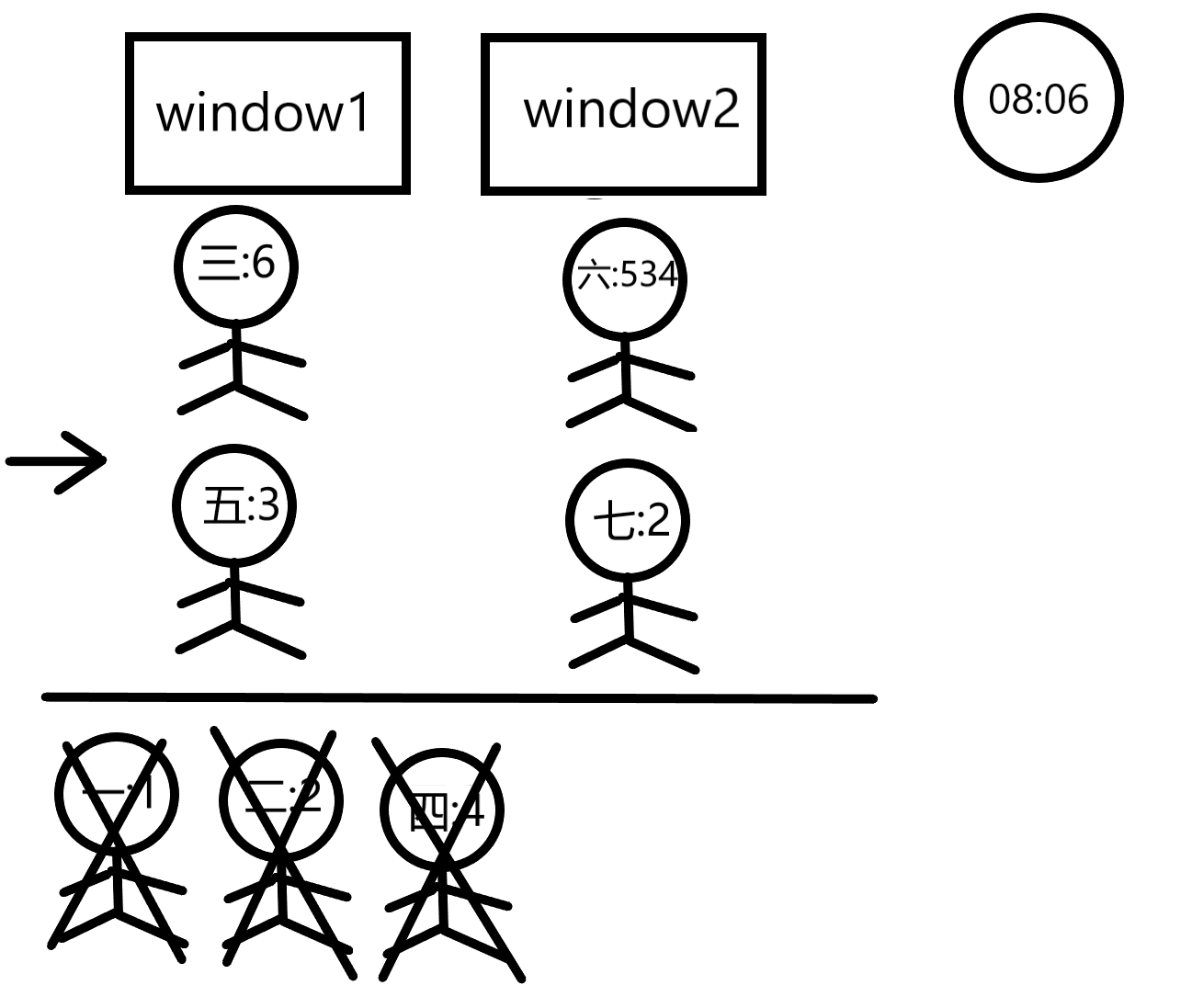
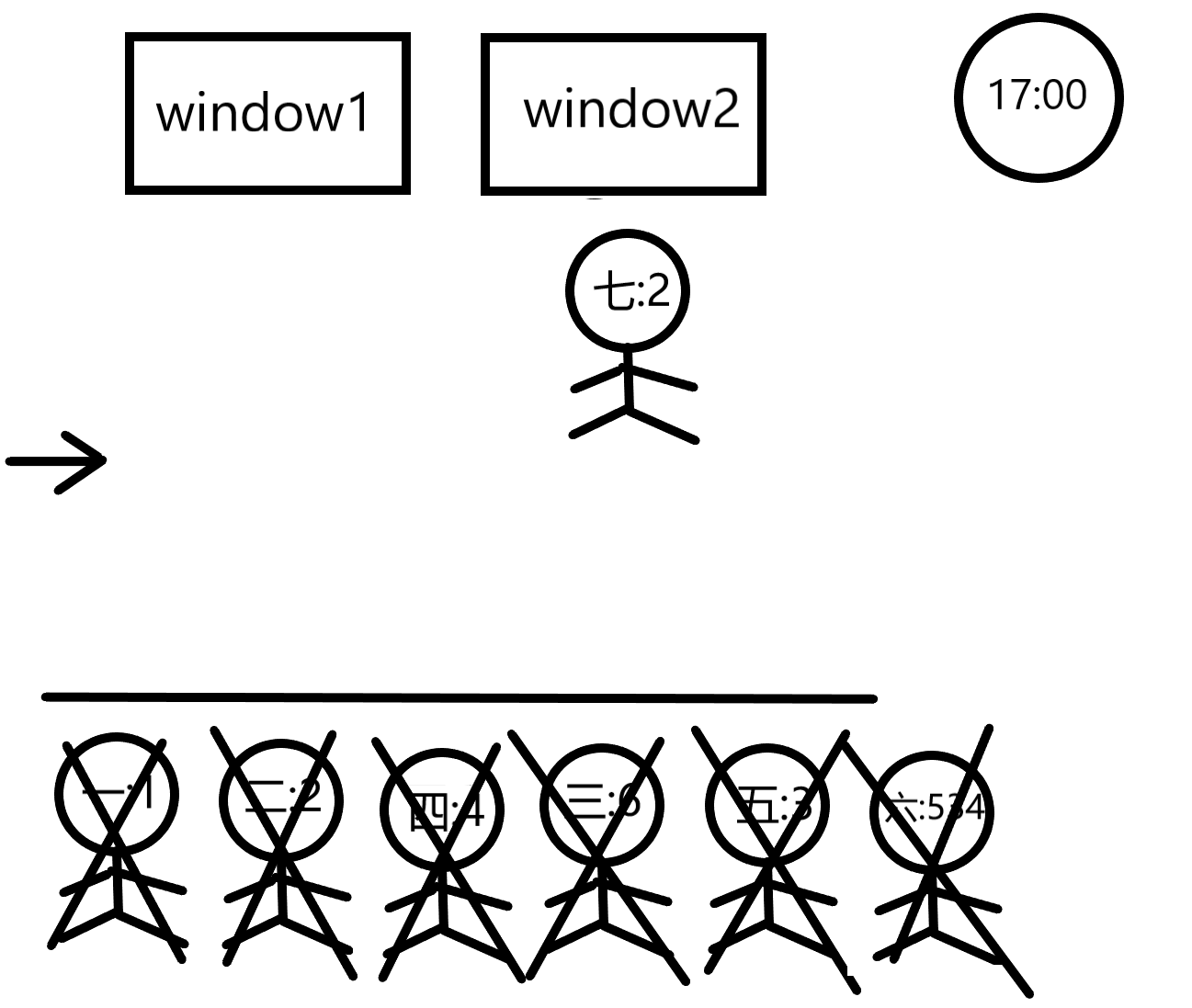
　　我们可以吧每一个窗口看作一个先进先出的队列，队列的容量为m，一共有n个这样的队列。queue<int> win[maxw]　，win[ i ]便代表第i窗口的队列。由于客户总是会选择最短的队列，所以在所有队列被填满时不会有出队操作。每个队列在开始处理今天第一名客户时记录现在以及消耗的时间为0，在所有队列都被填满后就要执行出队操作了，我们需要找到哪个窗口的客户先处理完，对其所在的窗口进行出队，同时获得当前处理的客户的结束时间与下一名客户的开始时间，之后将下一名客户入队。

　　在所有客户都入队后需要对所有窗口进行出队操作，这样便可以获得所有客户的开始时间与结束时间。

找到排队最短的窗口

int getMinSize(int &w){ //获得当前排队长度最短的窗口
    int minSize = INT_MAX;
    for(int i = ; i < n; i++){
        if(win[i].size() < minSize){
            minSize = win[i].size();
            w = i;
        }
    }
    return minSize;
}

　　找到最先处理完的客户所在的窗口并执行出队

void dispose(){ //找到最先处理完的客户所在的窗口并执行出队
    int disWin; //记录最先处理完的客户所在的窗口
    int disEdTime = INT_MAX;    //记录记录最先处理完的客户的结束时间
    for(int i = ; i < n; i++){
        if(disEdTime > nowTime[i] + needTime[win[i].front()]){
            //服务结束时间为当前窗口消耗时间假设处理该客户需要消耗的时间
            disWin = i; //记录窗口与结束时间
            disEdTime = nowTime[i] + needTime[win[i].front()];
        }
    }
    edTime[win[disWin].front()] = disEdTime;    //记录客户结束时间
    win[disWin].pop();  //出队
    nowTime[disWin] = disEdTime;    //记录该窗口现在已经消耗的时间
    if(!win[disWin].empty())
        bgTime[win[disWin].front()] = disEdTime;
        //下一名客户的开始时间就是上一名客户的结束时间
}

　　某窗口全部出队

void disposeAll(int w){ //处理某窗口全部出队
    while(!win[w].empty()){
        edTime[win[w].front()] = nowTime[w] + needTime[win[w].front()];
        //获得用户结束时间
        nowTime[w] = edTime[win[w].front()];
        //记录当前窗口消耗时间
        win[w].pop();
        if(!win[w].empty())//记录下一个用户的开始时间
            bgTime[win[w].front()] = nowTime[w];
    }
}

　　之后读入查询，判断所查询的客户的开始时间是否在17：00前，如果在17：00前输出其结束时间，否则输出Sorry。

AC代码

 #include <bits/stdc++.h>
 using namespace std;
 const int maxw = ;    //最大窗口数
 const int maxk = 1e3+;    //最大客户数
 queue<int> win[maxw];   //窗口队列
 int nowTime[maxw];  //记录每个窗口当前服务客户已经消耗的时间
 int needTime[maxk]; //记录服务每个客户需要消耗的时间
 int bgTime[maxk];   //记录每个客户开始被服务的时间
 int edTime[maxk];   //记录每个客户服务结束的时间
 int n, m, k, q; //n窗口数，m队列长度，k客户数，q查询数
 int getMinSize(int &w){ //获得当前排队长度最短的窗口
     int minSize = INT_MAX;
     for(int i = ; i < n; i++){
         if(win[i].size() < minSize){
             minSize = win[i].size();
             w = i;
         }
     }
     return minSize;
 }
 void dispose(){ //找到最先处理完的客户所在的窗口并执行出队
     int disWin; //记录最先处理完的客户所在的窗口
     int disEdTime = INT_MAX;    //记录记录最先处理完的客户的结束时间
     for(int i = ; i < n; i++){
         if(disEdTime > nowTime[i] + needTime[win[i].front()]){
             //服务结束时间为当前窗口消耗时间假设处理该客户需要消耗的时间
             disWin = i; //记录窗口与结束时间
             disEdTime = nowTime[i] + needTime[win[i].front()];
         }
     }
     edTime[win[disWin].front()] = disEdTime;    //记录客户结束时间
     win[disWin].pop();  //出队
     nowTime[disWin] = disEdTime;    //记录该窗口现在已经消耗的时间
     if(!win[disWin].empty())
         bgTime[win[disWin].front()] = disEdTime;
         //下一名客户的开始时间就是上一名客户的结束时间
 }
 void disposeAll(int w){ //处理某窗口全部出队
     while(!win[w].empty()){
         edTime[win[w].front()] = nowTime[w] + needTime[win[w].front()];
         //获得用户结束时间
         nowTime[w] = edTime[win[w].front()];
         //记录当前窗口消耗时间
         win[w].pop();
         if(!win[w].empty())//记录下一个用户的开始时间
             bgTime[win[w].front()] = nowTime[w];
     }
 }

 int main()
 {
     while(scanf("%d%d%d%d", &n, &m, &k, &q) != EOF){
         //输入n窗口数，m队列长度，k客户数，q查询数
         memset(nowTime, , sizeof(nowTime));
         memset(needTime, , sizeof(needTime));
         memset(edTime, , sizeof(edTime));
         memset(bgTime, , sizeof(bgTime));
         //将所有时间初始化为0
         for(int i = ; i <= k; i++){
             scanf("%d", &needTime[i]);
             //输入服务每个客户所需要的时间
         }
         int minSize, minWin;
         for(int i = ; i <= k; i++){    //遍历所有客户
             minSize = getMinSize(minWin);   //找到当前排队最短的窗口
             if(minSize >= m){   //如果所有窗口的队都满了
                 dispose();  //执行最先处理完客户所在的窗口出队
                 minSize = getMinSize(minWin);   //重新获得最短的队
             }
             win[minWin].push(i);    //入队
             if(win[minWin].empty()){    //每个窗口的第一个客户信息
                 nowTime[minSize] = ;   //当前窗口消耗时间为0
                 bgTime[i] = ;  //第一名客户的开始时间为0
             }
         }
         for(int i = ; i < n; i++){ //遍历所有窗口全部出队
             if(!win[i].empty()){
                 disposeAll(i);
             }
         }
         while(q--){ //获得查询
             int query;
             int endtime, begintime;
             scanf("%d", &query);
             endtime = edTime[query];
             begintime = bgTime[query];
             //获得查询用户的开始与结束时间
             int beginhours =  + (begintime / );
             int beginminutes = begintime % ;
             int endhours =  + (endtime / );
             int endminutes = endtime % ;
             if(beginhours >= ){   //开始时间大于17输出Sorry
                 printf("Sorry\n");
             }else
                 printf("%02d:%02d\n", endhours, endminutes);
         }
     }
     return ;
 }