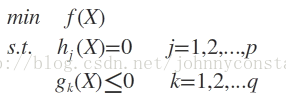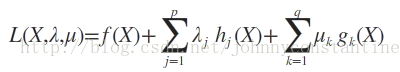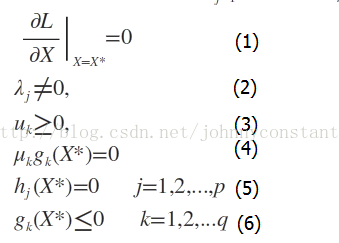SVM相关知识及和softmax区别
1.相对于容易过度拟合训练样本的人工神经网络,支持向量机对于未见过的测试样本具有更好的推广能力。
2.SVM更偏好解释数据的简单模型---二维空间中的直线,三维空间中的平面和更高维空间中的超平面。
3.SVM正是从线性可分情况下的最优分类面发展而来,主要思想就是寻找能够成功分开两类样本并且有最大分类间隔的最优分类超平面。算法最终转化为二次型寻优问题,得到的是全局最优,解决了在神经网络方法中无法避免的局部极值问题。
三类:对于样本中只有支持向量(SV)对超平面的划分有贡献,所以样本可由支持向量代替。(一般支持向量总是远远少于样本总数)
线性可分的SVM
非线性可分的SVM(C-SVM) 引入错误代价系数C
需要核函数映射情况下的SVM (通过非线性变换将其转化为某个高维空间中的线性问题) ---有个点积运算,可用核函数代替
核函数:
Kernel 函数满足Mercer条件,它就对应某一变换空间中的内积。
多类问题:
1 一对多的最大响应策略
2 一对一的投票策略
3 一对一的淘汰策略
(3)不等式约束条件
设目标函数f(x),不等式约束为g(x),有的教程还会添加上等式约束条件h(x)。此时的约束优化问题描述如下:
则我们定义不等式约束下的拉格朗日函数L,则L表达式为:
其中f(x)是原目标函数,hj(x)是第j个等式约束条件,λj是对应的约束系数,gk是不等式约束,uk是对应的约束系数。0
此时若要求解上述优化问题,必须满足下述条件(也是我们的求解条件):
这些求解条件就是KKT条件。(1)是对拉格朗日函数取极值时候带来的一个必要条件,(2)是拉格朗日系数约束(同等式情况),(3)是不等式约束情况,(4)是互补松弛条件,(5)、(6)是原约束条件。
对于一般的任意问题而言,KKT条件是使一组解成为最优解的必要条件,当原问题是凸问题的时候,KKT条件也是充分条件。
关于条件(3),后面一篇博客中给出的解释是:我们构造L(x,λ,u)函数,是希望L(x,λ,u)<=f(x)的(min表示求最小值)。在L(x,λ,u)表达式中第二项为0,若使得第三项小于等于0就必须使得系数u>=0,这也就是条件(3)。
关于条件(4),直观的解释可以这么看:要求得L(x,λ,u)的最小值一定是三个公式项中取得最小值,此时第三项最小就是等于0值的时候。稍微正式一点的解释,是由松弛变量推导而来。
参考: 支持向量机(SVM)复习总结
支持向量机原理(五)线性支持回归(待填坑)
SVM相关知识及和softmax区别的更多相关文章
- 面试之jsp、Servlet相关知识——生命周期, 区别等
1.servlet生命周期 所谓生命周期,指的是servlet容器如何创建servlet实例.分配其资源.调用其方法.并销毁其实例的整个过程. 阶段一: 实例化(就是创建servlet对象,调用构造器 ...
- 核函数以及SVM相关知识(重点)
http://www.cnblogs.com/jerrylead/archive/2011/03/18/1988406.html http://blog.pluskid.org/?p=685 考虑我们 ...
- iOS网络相关知识总结
iOS网络相关知识总结 1.关于请求NSURLRequest? 我们经常讲的GET/POST/PUT等请求是指我们要向服务器发出的NSMutableURLRequest的类型; 我们可以设置Reque ...
- 地址标记,SpringMVC转发与调用相关知识存档
1.mytest_mavenprj1中,index的 <a href="login/login.html">点击登录</a> 与 <a href=&q ...
- AJAX跨域调用相关知识-CORS和JSONP(引)
AJAX跨域调用相关知识-CORS和JSONP 1.什么是跨域 跨域问题产生的原因,是由于浏览器的安全机制,JS只能访问与所在页面同一个域(相同协议.域名.端口)的内容. 但是我们项目开发过程中,经常 ...
- 【转载】前端面试“http全过程”将所有HTTP相关知识抛出来了...
原文:前端面试“http全过程”将所有HTTP相关知识抛出来了... 来一篇串通,一个http全过程的问题,把所有HTTP相关知识点都带过一遍 http全过程 输入域名(url)-->DNS映射 ...
- HTML入门基础教程相关知识
HTML入门基础教程 html是什么,什么是html通俗解答: html是hypertext markup language的缩写,即超文本标记语言.html是用于创建可从一个平台移植到另一平台的超文 ...
- Python 数据分析(二 本实验将学习利用 Python 数据聚合与分组运算,时间序列,金融与经济数据应用等相关知识
Python 数据分析(二) 本实验将学习利用 Python 数据聚合与分组运算,时间序列,金融与经济数据应用等相关知识 第1节 groupby 技术 第2节 数据聚合 第3节 分组级运算和转换 第4 ...
- Svm相关
Svm相关: 1) SVM方法是通过一个非线性映射p,把样本空间映射到一个高维乃至无穷维的特征空间中(Hilbert空间),使得在原来的样本空间中非线性可分的问题转化为在特征空间中的线性可分的问题. ...
随机推荐
- 一步步制作RPM包
一步步制作RPM包 来源 http://blog.51cto.com/laoguang/1103628 一.RPM制作步骤 我们在企业中有的软件基本都是编译的,我们每次安装都得编译,那怎么办呢?那就根 ...
- 股神小L [贪心]
题面 思路 股票题肯定是贪心或者$dp$啊 这个题比较$naive$,可以看出来你这里买股票的过程一定是能不买就不买,能卖就拣最贵的日子卖,而且时间不能倒流(废话= =||) 所以我们按照时间从前往后 ...
- HDU 5761 物理题
Rower Bo Time Limit: 2000/1000 MS (Java/Others) Memory Limit: 131072/131072 K (Java/Others)Total ...
- 导入android源码中的APP源码到eclipse
导入android源码中的APP源码到eclipse 一般最简单的办法就是创建新的android工程,选择create project from existing source选项,直接导入源码就OK ...
- NetAPP常用操作
===CIFS share======================================================================================= ...
- mysql5.6免安装配置(菜鸟版)
mysql5.6免安装配置 MySQL5.6.13安装步骤(Windows7 32位) 1. 下载MySQL Community Server 5.6.13 2. 解压MySQL压缩包 将以下载的My ...
- bzoj4418 [Shoi2013]扇形面积并
传送门:http://www.lydsy.com/JudgeOnline/problem.php?id=4418 [题解] 被题目名称吓死系列. 用一棵线段树维护当前有哪些半径. 那么将扇形差分,每段 ...
- 昨天用到的一个sql查询。可取处,用max
SELECT T_AssetInfos_ID, MAX(T_AssetConstruct_Name), MAX(T_AssetProperties_Name), SUM(CAST(PropertyVa ...
- linux下修改mysql数据库编码后无法启动解决办法
linux下老版本的Mysql修改数据库编码的方法是 修改my.cnf vi /etc/my.cnf 在[client]下添加 default-character-set=utf8 在[mysqld] ...
- Linux之epoll详细解析实现
/* * fs/eventpoll.c (Efficient event retrieval implementation) * Copyright (C) 2001,...,2009 Davide ...