[SinGuLaRiTy] 2017-07-26 综合性测试

【SinGuLaRiTy-1032】 Copyright (c) SinGuLaRiTy 2017. All Rights Reserved.

             

单词 (word)

题目描述

有一个有字母表，一共有N行M列，你从左上角开始出发，目的地是右下角。每次你只能往右或往下走一步。将你经过的格子里面的字母按照访问顺序组成一个单词。求你能得到的字典序最小的单词是什么？

输入

第一行包含N和M，（1<=N,M<=2000）
接下来N行，每行包含M个小写字母。

输出

输出最小字典序的单词。
40%的数据，每个格子的右、下的字母不同。

样例数据

样例输入1	样例输出1
4 5 ponoc ohoho hlepo mirko	pohlepko
样例输入2	样例输出2
4 5 bbbbb bbbbb bbabb bbbbb	bbbbabbb
样例输入3	样例输出3
2 5 qwert yuiop	qweiop

<样例解释>

对于样例一，下面表示了一种字典序最小的解法：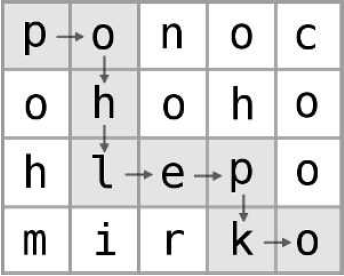

解析

如果往右或往下的不一样，那么没的说，直接往字典序小的走就行了。
不过，当当前位置上，往左或往下的一样的时候，问题就来了——我们在当前是不能确定往右还是往左的。对此，每走一步，我们可以开一个列表，来保存在一定步数后我们能到达的所有的最佳位置。我们从一个包含初始字符(0,0)的列表开始，在接下来的每一步中更新列表，便于我们查询当前列表中所有位置的邻位的最小字典序的值，然后创建一个所有具有这个最小值的邻位的位置。因为我们可以通过两种方式到达一个位置，我们需要注意到不要将同一个位置重复放入列表中，否则我们将在每一次迭代中复制相同位置的出现次数。

Code

#include<iostream>
#include<cstdio>
#include<vector>
#include<cstdlib>
#include<algorithm>
#include<cstring>

using namespace std;

typedef pair<int, int> point;

#define x first
#define y second

const int MAX=;

int n,m;
char grid[MAX][MAX];
bool vis[MAX][MAX];

int main(void)
{
    scanf("%d%d",&n,&m);
    for(int i=;i<n;i++)
        scanf("%s",grid[i]);

    vector<point> curr,next;
    for(curr.push_back({,});!curr.empty();curr=next)
    {
        point p=curr.back();
        printf("%c",&grid[p.x][p.y]);
        char mn='z';
        for(point pt : curr)
        {
            int dx=,dy=;
            for(int i=;i<;i++)
            {
                swap(dx,dy);
                int nx=pt.x+dx;
                int ny=pt.y+dy;
                if(nx>=n||ny>=m)
                    continue;
                mn=min(mn,grid[nx][ny]);
            }
        }
        next.clear();
        for(point pt : curr)
        {
            int dx=,dy=;
            for(int i=;i<;i++)
            {
                swap(dx,dy);
                int nx=pt.x+dx;
                int ny=pt.y+dy;
                if(nx>=n||ny>=m)
                    continue;
                if(vis[nx][ny])
                    continue;
                if(grid[nx][ny]==mn)
                {
                    next.push_back({nx,ny});
                    vis[nx][ny]=;
                }
            }
        }
    }
    return ;
}

玻璃杯 (drink)

题目描述

你有N个容量无限大的玻璃杯，每个玻璃杯都有一些水。你想要喝光所有的水，但是你最多只能喝k个玻璃杯。怎么办呢？你可以把一个玻璃杯的水全部倒入另一个玻璃杯，。但是你将第i个玻璃杯中的水倒入第j个玻璃杯，需要花费代价Cij。如何花费最少的代价，让你能喝光所有的水。

输入

第一行包含整数N,K(1<=K<=N<=20)；
接下来N行，每行包含N个整数Cij(0<=Cij<=10^5)。第i行第j列的数表示Cij。Cii一定是0.

输出

输出最小的代价。
40%的数据，N<=10。

样例数据

样例输入1	样例输出1
3 3 0 1 1 1 0 1 1 1 0	0
样例输入2	样例输出2
3 2 0 1 1 1 0 1 1 1 0	1
样例输入3	样例输出3
5 2 0 5 4 3 2 7 0 4 4 4 3 3 0 1 2 4 3 1 0 5 4 5 5 5 0	5

解析

这是一道DP题。我们可以用一个20位的二进制数来表示当前的玻璃杯的状态。我们可以做的，就是将一个玻璃杯里的水倒出到另一个杯子里，状态转移的时间复杂度为O(N^2)，不过通过优化似乎可以跑的更快。总时间复杂度就是O(2*N*N^2).

Code

#include<cstdio>
#include<string>
#include<vector>
#include<map>
#include<cstdlib>
#include<algorithm>
#include<cstring>

using namespace std;

typedef pair <int, int> pii;

const int MAXN = ;

int n, k;
int a[MAXN][MAXN];
int dp[<<MAXN];

int solve(int mask)
{
    if(__builtin_popcount(mask)==k)
        return ;
    int &ret=dp[mask];
    if(ret!=-)
        return ret;
    ret=<<;
    for(int i=;i<n;++i)
    {
        if(!(mask&(<<i)))
            continue;
        for(int j=;j<n;++j)
        {
            if(i==j)
                continue;
            if(!(mask&(<<j)))
                continue;
            ret=min(ret,solve(mask^(<<i))+a[i][j]);
        }
    }
  return ret;
}

int main()
{
    memset(dp,-,sizeof dp);
    scanf("%d%d",&n,&k);
    for(int i=;i<n;++i)
        for(int j=;j<n;++j)
            scanf("%d",&a[i][j]);
    printf("%d",solve((<<n)-));
    return ;
}

数列 (sequence)

题目描述

你有N个正整数，开始时，你在黑板上写下第一个数，写第二个数时，你可以在第一个数的左边写，也可以在第一个数的右边写。你每写一个数，都可以选择在前面已经写过的数的左边或者右边的位置。不同的写法可以得到不同的数列。在所有可能得到的数列中找出最长的上升子序列，求出它的长度。设它的长度为M,你还需求出长度为M的上升子序列有多少种？注意：在不同的数列中的最长上升子序列都是不同的；即使在同一个数列中的两个最长上升子序列，只要有一个数的位置不一样，也算不同的子序列。

输入

第一行一个整数N（1<=N<=2*10^5）
接下来N个空格隔开的整数，表示你拥有的N个数。每一个数均不超过10^9。

输出

只有一行，包含两个数，第一个数为最长的上升子序列的长度。

样例数据

样例输入1	样例输出1
2 1 1	1 4
样例输入2	样例输出2
4 2 1 3 4	4 1

<样例解释>

样例数据一：

最长上升子序列长度为1.
首先有两种写的顺序，第一种是第二个数在第一个数的左边，第二种是第二个数在第一个数的右边。在每一种中，你可以选择第一个数作为最长上升子序列，也可以选择第二个数作为最长上升子序列。所以一共有4种。

样例数据二：

你有八种写的顺序。但是只有一种顺序能够得到最长上升子序列，即1 2 3 4，其中的最长上升子序列是唯一的。所以答案是4 1.

<数据范围>

30%的数据，N<=20
50%的数据，N<=1000

解析

为了确定最长上升子序列的长度，对于初始序列中的每一个位置X，必须确定从X的右侧开始并终止于X的最长上升子序列的长度(序列从右到左读取)，以及我们达到这个状态的方法的数量。这个思路也同样适用于最长下降子序列。我们可以通过相对简单的方法来实现，即使用Fenwick Tree的数据结构，时间复杂度为O(N*logN)。
我们会注意到，解决方案是严格上升子序列和严格下降子序列的并集，其中上升子序列的最大元素小于下降子序列的最小元素。如果A是在位置X(包含X)结束的严格上升子序列的长度，B也是在位置X(包含X)结束的严格下降子序列的长度，num_A,num_B分别是得到它们的方法数，那么X(包含X)右侧的数字的最大长度就是A+B-1，得到这个解的方法数为num_A*num_B。
所要求的最大长度就是每一个位置对应的最大长度的最大值。我们用R来表示这个最大值。我们能达到这个最大长度的方法数，就是对应的最大长度等于R*(2N-R)的当前位置的方案数的乘积。
其中的2N-R是必要的，因为如果一个解包含R个数，那么剩下的N-R个数当中的每一个都可以被独立地放置在之前的所有数的前面或后面。
解法的总时间复杂度为O(N*logN)。

Code

#include<iostream>
#include<cstdio>
#include<vector>
#include<algorithm>

using namespace std;

typedef long long int ll;
typedef pair<int, int> par;

#define X first
#define Y second

const int MAXN=,MOD=;

inline int add(int a,int b)
{
    int ret=a+b;
    if(ret>=MOD)
        ret-=MOD;
    return ret;
}

inline int mul(int a,int b)
{
    ll ret=(ll)a*b;
    if(ret>=MOD)
        ret%=MOD;
    return ret;
}

int n;
int niz[MAXN],dva[MAXN];

par A[MAXN],B[MAXN];
par FWT_up[MAXN],FWT_down[MAXN];

par rj;

par point(par a,par b)
{
    if(b.X>a.X)
    {
        a.X=b.X;
        a.Y=b.Y;
    }
    else if(b.X==a.X)
        a.Y=add(a.Y,b.Y);
    return a;
}

void put_up(int x,par v)
{
    x+=;
    for(;x<MAXN;x+=x&-x)
        FWT_up[x]=point(FWT_up[x],v);
}

par query_up(int x)
{
    x+=;
    par ret(,);
    for(;x>;x-=x&-x)
        ret=point(ret,FWT_up[x]);
    return ret;
}

void put_down(int x,par v)
{
    x+=;
    for(;x>;x-=x&-x)
        FWT_down[x]=point(FWT_down[x],v);
}

par query_down(int x)
{
    x+=;
    par ret(,);
    for(;x<MAXN;x+=x&-x)
        ret=point(ret,FWT_down[x]);
    return ret;
}

void work()
{
    vector<int> v;
    for(int i=;i<n;i++)
        v.push_back(niz[i]);
    sort(v.begin(),v.end());
    v.resize(unique(v.begin(), v.end())-v.begin());
    for(int i=;i<n;i++)
        niz[i]=lower_bound(v.begin(),v.end(),niz[i])-v.begin();
}

void mid_up()
{
    for(int i=n-;i>=;i--)
    {
        par p=query_up(niz[i]-);
        if(p.X==)
        {
            A[i]=par(,);
            put_up(niz[i],par(,));
        }
        else
        {
            A[i]=p;
            p.X++;
            put_up(niz[i],p);
        }
    }
}

void mid_down()
{
    for(int i=n-;i>=;i--)
    {
        par p=query_down(niz[i]+);
        if(p.X==)
        {
            B[i]=par(,);
            put_down(niz[i],par(,));
        }
        else
        {
            B[i]=p;
            p.X++;
            put_down(niz[i],p);
        }
    }
}

void fang()
{
    dva[]=;
    for(int i=;i<MAXN;i++)
        dva[i]=mul(dva[i-],);
}

void Main()
{
    for(int i=;i<n;i++)
        rj=point(rj,par(A[i].X++B[i].X,mul(A[i].Y,B[i].Y)));
    rj.Y=mul(rj.Y,dva[n-rj.X]);
}

int main()
{
    fang();
    scanf("%d",&n);
    for(int i=;i<n;i++)
        scanf("%d", &niz[i]);
    work();
    mid_up();
    mid_down();
    Main();
    printf("%d %d\n",rj.X,rj.Y);
    return ;
}

Time: 2017-07-26