吴恩达机器学习笔记（三） —— Regularization正则化

主要内容：

一.欠拟合和过拟合(over-fitting)

二.解决过拟合的两种方法

三.正则化线性回归

四.正则化logistic回归

五.正则化的原理

一.欠拟合和过拟合(over-fitting)

1.所谓欠拟合，就是曲线没能很好地拟合数据集，一般是由于所选的模型不适合或者说特征不够多所引起的。

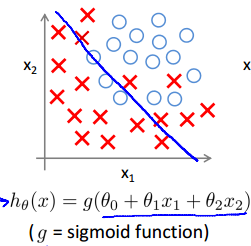
2.所谓过拟合，就是曲线非常好地拟合了数据集（甚至达到完全拟合地态度），这貌似是一件很好的事情，但是，曲线千方百计地去“迎合”数据集，就导致了其对其他数据的预测性或者说通用性不高。这就好像，期末考试前，老师指明了考试内容，同学千方百计地去复习这些内容，于是就就很容易拿到高分，这就可以理解为过拟合，但当以后要用到这一门科目的其他知识的时候，之前的复习的用处就大打折扣了，因为基本没有触及到其他知识，即期末考试前的“复习”只迎合了期末考试，但对以后的帮助不大，通用性不高。

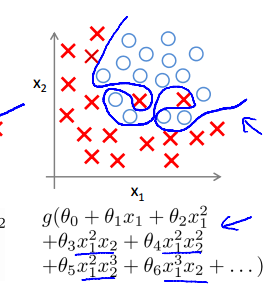
二.解决过拟合的两种方法

1.减少特征数（feature）：可知，当特征x1、x2……xn的数量n越多时，就越容易拟合数据集（特征越多，曲线越弯曲，伸缩性越大）。所以为了防止过拟合，可以手工地去掉一些特征或者利用一些算法自动筛选出特征。比如，预测房子价格时，有大小和房间数两个特征，这时可以去掉房间数这个特征以避免过拟合。

2.正则化：正则化可以保留下所有的特征，但是需要对参数做一些“惩罚”，这个“惩罚”就是降低参数的数量级，事实证明（别人说的，人云亦云的我）：当参数的值处以一个较小的范围内时，曲线相对平滑，也就可以避免过拟合了。至于如何“惩罚”，请看下文。

三.正则化线性回归

我们在损失函数的后面加多一项：

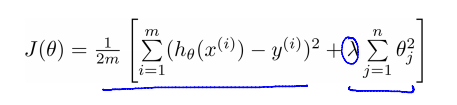
向量化后：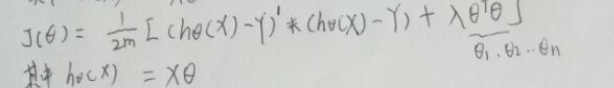

这一项就叫做“正则项”，起到了惩罚参数的作用。注意j是1开始到n，即不惩罚θ0，具体原因现在还不清楚。

其中λ调节着正常项与正则项在损失函数中所占的比重，当λ过大时，正则项所占的比重就会很大，导致参数的数量级很小，甚至接近于0，出现欠拟合的现象。

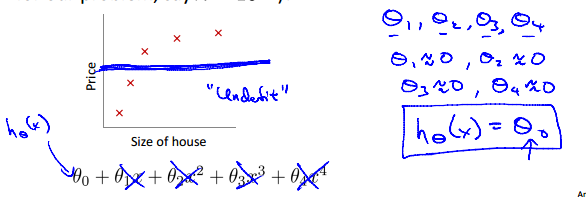
正则化后的梯度下降为：

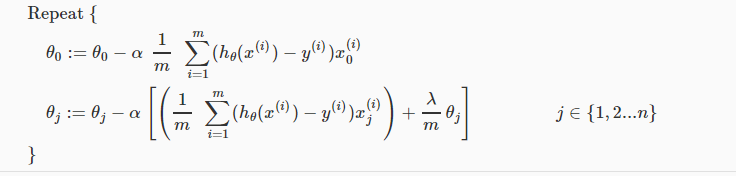
对于上式θj（1<=j<=n），将其进一步化简，得：

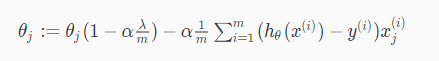
其中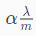是一个小于1的正数（具体原因现在还不清楚）。在每次迭代的时候，θj都是先乘以一个小于1的倍数再去减那一堆东西，所以相比没有正则化，正则化后的就更容易变小了（模模糊糊的）。

向量化后：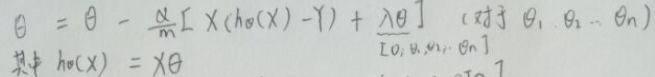

（注意：正则项的Θ0应该改为0，表明不惩罚Θ0）

而对于最小二乘法，就变为了：

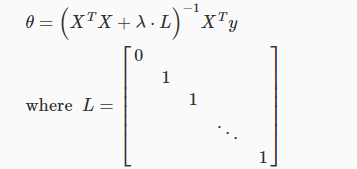
四.正则化logistic回归

加入正则项后：

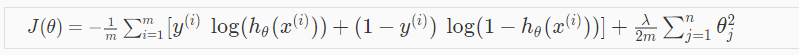
向量化后：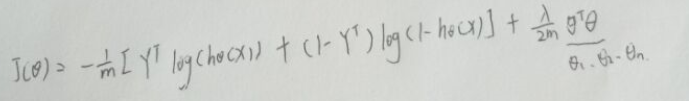

梯度下降就变为：

向量化后：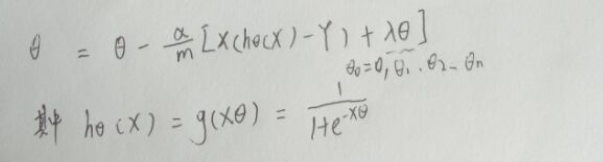

五.正则化的原理

在损失函数里加多一个λθ^2，就可以对参数θ进行惩罚，降低θ的数量级，这是为什么呢？有什么数学的解释？

答：自己想到一个。当θ越靠近0时，θ^2越小；当θ越远离0时，θ^2越大。所以在最小化损失函数的过程中，λθ^2这一项有拉低θ的数量级的作用（使得θ往0的方向靠近），从而对参数θ进行惩罚。