机器学习：SVM（基础理解）

一、基础理解

　1）简介

• SVM（Support Vector Machine）：支撑向量机，既可以解决分类问题，又可以解决回归问题；
• SVM 算法可分为：Hard Margin SVM、Soft Margin SVM，其中 Soft Margin SVM 算法是由 Hard Margin SVM 改进而来；

　2）不适定问题

• 不适定问题：决策边界不唯一，可能会偏向某一样本类型，模型泛化能力较差；

• 具有不适定问题的模型的特点：决策边界不准确，泛化能力较差；

• 原因：模型由训练数据集训练所得，训练数据集并没有包含所有类型的所有样本，训练数据集的样本的分布，可能不能准确的反应不同类型的样本分布的真正规律，由训练数据集得到模型，该模型的决策边界也很可能不是真正的分类边界；这样的话，该模型的决策边界会偏向某一样本类型，使模型泛化能力较差。

　3）逻辑回归中的 不适定问题

• 逻辑回归思想：定义一个概率函数，根据概率函数进行建模，形成损失函数，最小化损失函数得到决策边界；

• 决策边界可能是多种情况：
• 

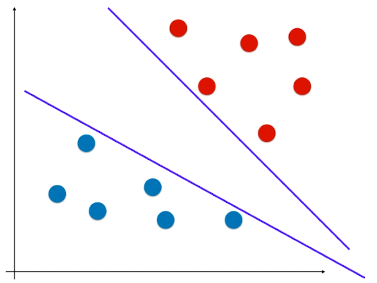
• 如图：如果有一个样本，离红色类型较近，离蓝色类型较远，但由于决策边界偏向红色类型，模型会判断该样本为蓝色类型：
• 

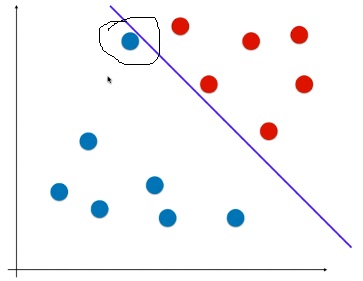
　4）SVM 算法的思想

• 解决“不适定问题”；
• 目的：找到一个最优决策边界，不仅很好的划分训练数据集，又有很好的泛化能力；
• 方法：让该决策边界离两种类别的样本都尽可能的远；

1. 或者说，在逻辑回归的决策边界的基础上，让离直线最近的点尽可能的远（如图离直线较近的 3 个点）
2. 

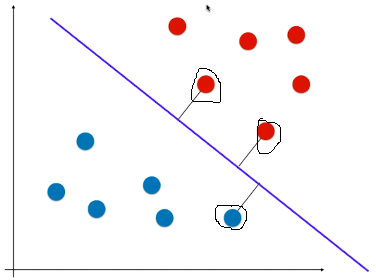
• 思想：SVM 在考虑未来模型的泛化能力时，没有寄望在数据的预处理阶段，或者模型的正则化手段上；而是将泛化能力的考量直接放在了算法的内部，找到一条决策边界，决策边界离不同类型的样本都尽可能的远；

• 疑问：为什么离两种类别的样本都尽可能的远的直线，能对该两类样本更好的划分？

• 原因：直观来看，这种决策边界的泛化能力较好，但这种假设不仅仅根据直观的现象，其背后也有数学理论；（数学中可以证明，面对“不适定问题”，这种方法找到的决策边界，对应的模型的泛化能力较好）正是由于这种原因，SVM 也是统计学中重要的方法，其背后有极强的统计理论知识的支撑；

　5）SVM 实现的具体方法

• 决策边界就是根据支撑向量和 margin 所得；

1. 支撑向量：特征空间中，距离决策边界最近的不同类型的样本点；（如图所示）
2. margin：如图所示，特征空间中，由两类支撑向量决定的两条线的距离；
3. 如图：决策边界为中间的那天线；
4. margin = 2d
5. 

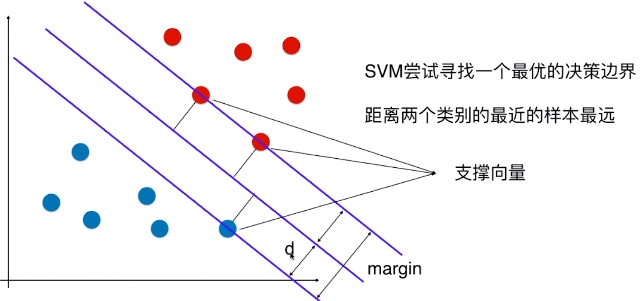
• SVM 算法本质就是要最大化 margin；

　6）线性可分、Hard Margin SVM、Soft Margin SVM

• 不管是讨论逻辑回归算法还是 SVM 算法，前提是：样本分布线性可分；

• 线性可分：对于特征空间，存在一条直线或一个平面将样本完全分开

• Hard Margin SVM：

1. 解决线性可分问题的 SVM 算法；
2. 非常严格的，确实找到了一个决策边界，没有错误的将样本点进行了划分，同时最大化了 margin 的值；

• Soft Margin SVM：

1. 解决线性不可分的问题；
2. 实践中，大多真实的样本数据是线性不可分的；
3. Soft Margin SVM 算法是从 Hard Margin SVM 的基础上改进的；