codeforces-505B

题目连接：http://codeforces.com/contest/505/problem/B

B. Mr. Kitayuta's Colorful Graph

time limit per test

1 second

memory limit per test

256 megabytes

input

standard input

output

standard output

Mr. Kitayuta has just bought an undirected graph consisting of n vertices and m edges. The vertices of the graph are numbered from 1 to n. Each edge, namely edge i, has a color ci, connecting vertex ai and bi.

Mr. Kitayuta wants you to process the following q queries.

In the i-th query, he gives you two integers — ui and vi.

Find the number of the colors that satisfy the following condition: the edges of that color connect vertex ui and vertex vi directly or indirectly.

Input

The first line of the input contains space-separated two integers — n and m (2 ≤ n ≤ 100, 1 ≤ m ≤ 100), denoting the number of the vertices and the number of the edges, respectively.

The next m lines contain space-separated three integers — ai, bi (1 ≤ ai < bi ≤ n) and ci (1 ≤ ci ≤ m). Note that there can be multiple edges between two vertices. However, there are no multiple edges of the same color between two vertices, that is, if i ≠ j,(ai, bi, ci) ≠ (aj, bj, cj).

The next line contains a integer — q (1 ≤ q ≤ 100), denoting the number of the queries.

Then follows q lines, containing space-separated two integers — ui and vi (1 ≤ ui, vi ≤ n). It is guaranteed that ui ≠ vi.

Output

For each query, print the answer in a separate line.

Examples

input

4 51 2 11 2 22 3 12 3 32 4 331 23 41 4

output

210

input

5 71 5 12 5 13 5 14 5 11 2 22 3 23 4 251 55 12 51 51 4

output

11112

Let's consider the first sample.

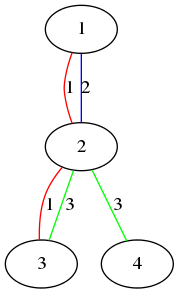The figure above shows the first sample.

• Vertex 1 and vertex 2 are connected by color 1 and 2.
• Vertex 3 and vertex 4 are connected by color 3.
• Vertex 1 and vertex 4 are not connected by any single color.

题目大意：给定一个图，可能存在重边，各边有不同权值，给定任意两点，求两点之间有多少种相同权值的边相连。解题思路：题目很直白，有多种解法，因为数据范围很小，所以可以直接对于每种颜色dfs遍历一遍，因为有多次查询，所以综合考虑为节省时间直接全部dfs一遍，再将结果储存在一个二维数组中，每次查询输出数组中的结果即可。因为可能存在重边，所以使用vector存边。dfs很简单，每次寻找一种颜色即可。代码如下：

#include<bits/stdc++.h>

using namespace std;

vector <][];
int n;
]= {};

bool dfs(int now,int color,int e)
{
    if(now==e)
        return true;
    ; i<=n; i++)
    {
        )
            continue;
        ; j<g[now][i].size(); j++)
        {
            if(g[now][i][j]!=color)
                continue;
            else
            {
                vis[i]=;
                if(dfs(i,color,e))
                    return true;
            }
        }
    }
    return false;
}

int main()
{
    int m,u,v,c,q,ans;
    ][];
    scanf("%d%d",&n,&m);
    ; i<m; i++)
    {
        scanf("%d%d%d",&u,&v,&c);
        g[u][v].push_back(c);
        g[v][u].push_back(c);
    }
    ; i <= n; i++)
    {
        ; j <= n; j++)
        {
            ans = ;
            ; k <= m; k++)
            {
                memset(vis,,sizeof(vis));
                if (dfs(i, k, j))
                    ans++;
                mp[i][j] = mp[j][i] = ans;
            }
        }
    }
    scanf("%d",&q);
    ; i<q; i++)
    {
        scanf("%d%d",&u,&v);
        cout<<mp[u][v]<<endl;
    }
}

此题还可以用并查集来解，构造一个二维并查集，每个颜色分别记录，更简单而且更快，但是第一时间想到的就是dfs，以后做题思维应当更灵活，不能定式思维，要熟悉各个算法可以实现的各种功能，再多加思考选用最优解。