systemverilog中实现饱和截位和饱和截位的分析

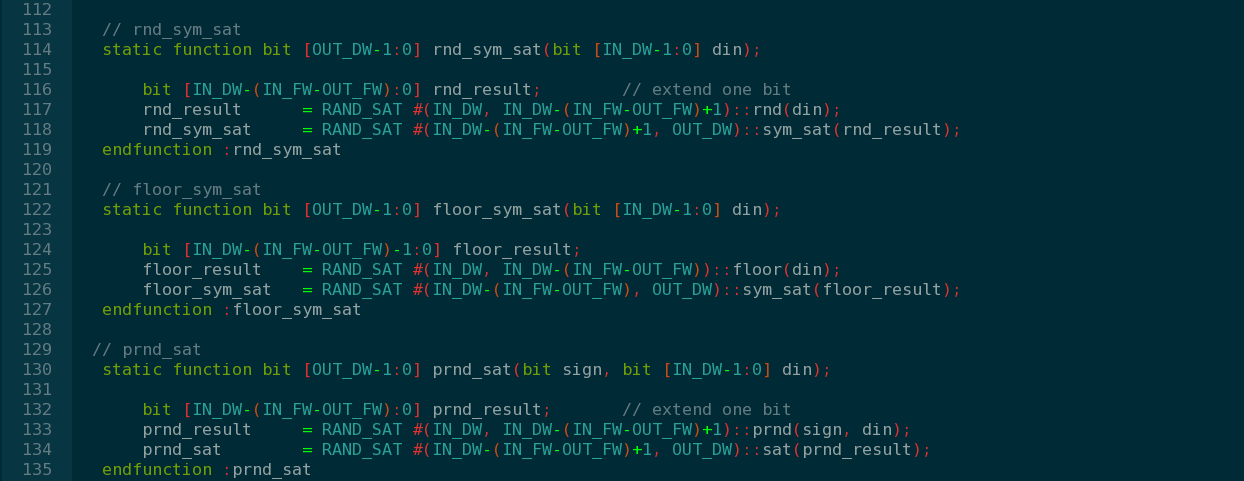
截位（rnd/prnd/floor）:都是去掉低位数据的操作（去掉低位低精度的数据，或者说小数位，降低数据的精度）

饱和（sat/sym_sat）:都是去掉高位数据的操作，（去掉无符号数高位的0，或者有符号数高位多余的符号位）

函数说明：

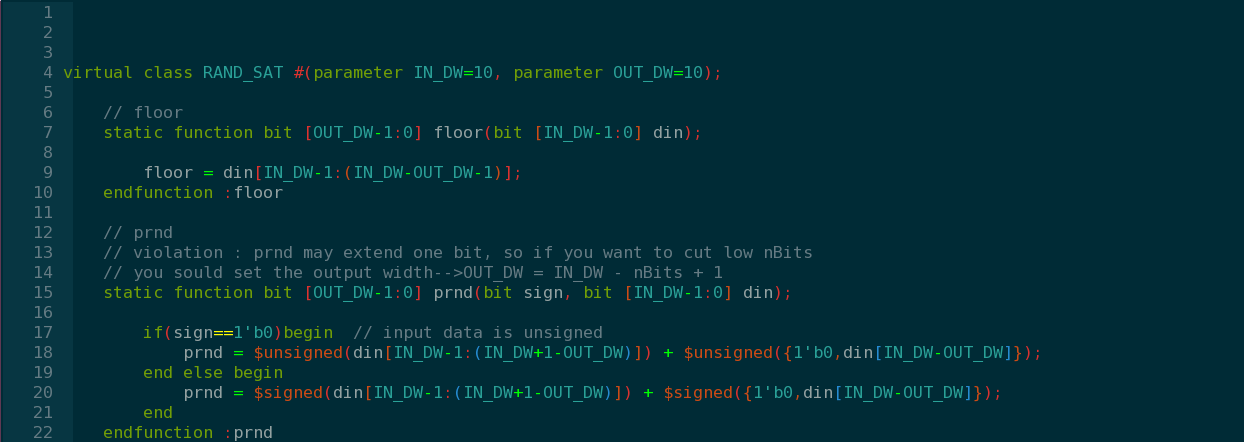
floor：

1、这个操作很简单，就是把低位直接截掉，精度损失大。有符号和无符号数据都适用用于这个函数，且不需要指示输入的数据是有符号还是无符号。

prnd：

1、一种四舍五入处理，对于正数，是大于等于0.5就加1，否则去掉小数位；对于负数则是大于0.5就加1，否则去掉小数位。prnd（+x.5）=x+1、prnd（+x.499..99）=x、prnd（-x.5）=-x，prnd（-x.50.....01）=-(x+1)

2、prnd可以处理无符号和有符号数据，输入要指示数据的类型，sign=0表示无符号，sign=1表示有符号数据。

3、prnd处理有加法操作，会扩宽数据位宽，比如一个6bit的数据，你想截掉低3位数据，那么输出的数据位宽应该是4bit，OUT_DW = IN_DW - nBits + 1，4 = 6 - 3 + 1.

rnd：

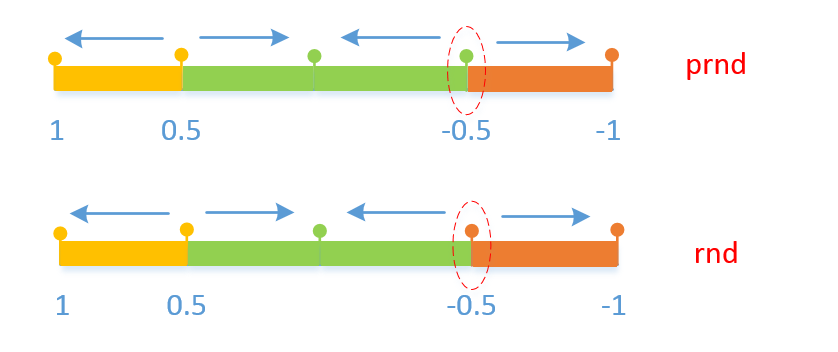
1、一种四舍五入的处理，对于正数和负数都是小数大于等于0.5就加1，否则去掉小数位。rnd（+x.5）=x+1、rnd（+x.499..99）=x、rnd（-x.5）=-(x+1)，rnd（-x.499...99）=-x

2、rnd的处理是关于原点对称的，而prnd的处理不是关于原点对称的。在ASIC处理中，prnd相对简单些，rnd要复杂些，但是两种处理后保留的精度是一样的，不存在prnd好于rnd的说法。只有一些需要将数据处理成原点对称，用于RM比较的时候才会用到rnd。比如RM的处理顺序是先取反后截位，ASIC的处理是先截位后取反，这个时候截位就必须要使用rnd，因为取反是关于原点对称的处理，rnd才有会有，-rnd(a)=rnd(-a)

3、rnd与prnd的唯一不同点就是在小数-0.5的截位上，prnd是截成-1，rnd是截成-2.

4、将数据分为保留部分preserve_part和截去部分cut_part

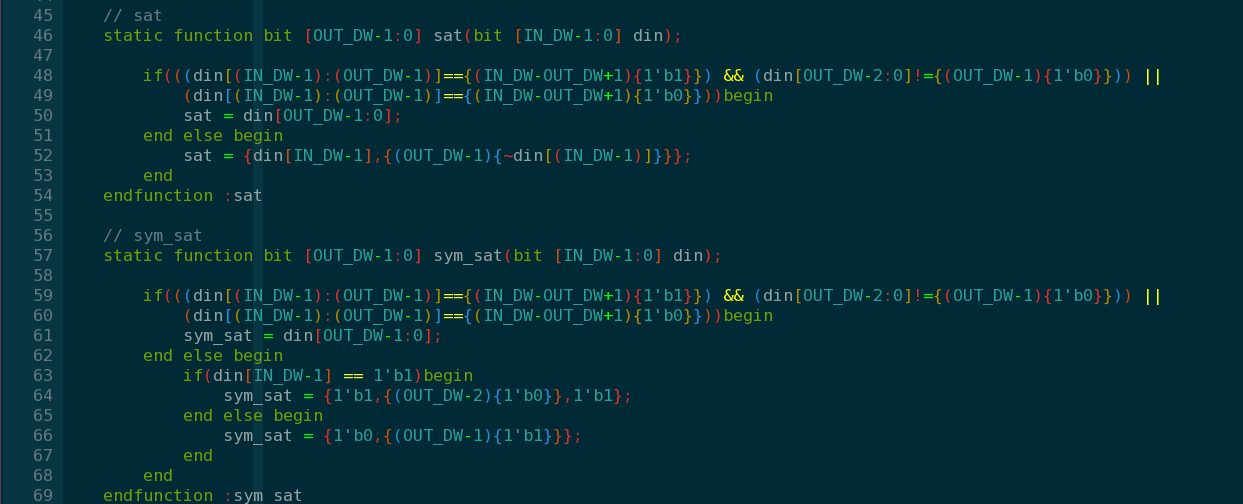
sat:

1、sat直接去掉有符号数的高位符号，或者无符号数据高位的0，如果发现溢出了，就把数据保持为最大的正数或者负数。

sym_sat:

1、相比sat，多了一个对称的操作，就是数据如果是最大的负数要设为最大负数-1，负数溢出了也只保持到最大负数-1。这样做的目的也rnd一样，就是为了保证数据处理的对称性。

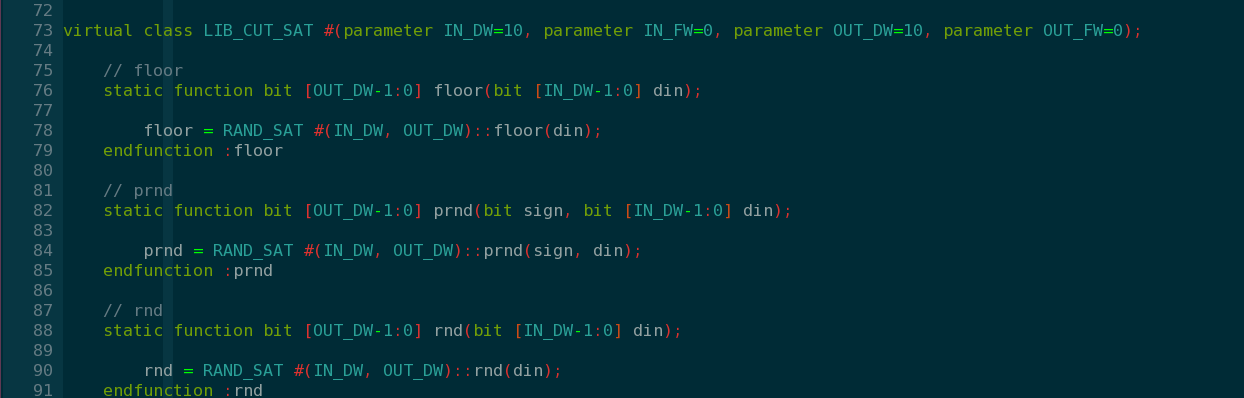
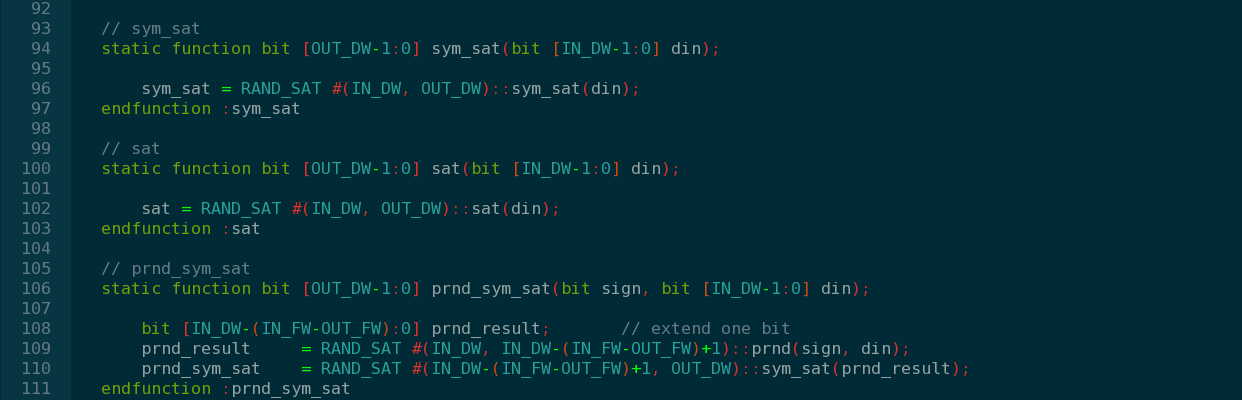
RAND_SAT/LIB_CUT_SAT:

1、RAND_SAT类中，实现了基本的饱和截位处理，有的时候要连续使用两种处理，且中间会有扩位，就把额外添加了一个LIB_CUT_SAT类。