转自：昵称：python修行路

https://www.cnblogs.com/zhaof/p/7326260.html

爬虫---爬虫er与反爬虫er之间的斗争 转发的更多相关文章

  1. JAVA爬虫对font-face字体反爬虫解密

    1.参考博客          https://www.jianshu.com/p/9975de57b0ce          https://blog.csdn.net/litang199612/a ...

  2. 反反爬虫 IP代理

    0x01 前言 一般而言,抓取稍微正规一点的网站,都会有反爬虫的制约.反爬虫主要有以下几种方式: 通过UA判断.这是最低级的判断,一般反爬虫不会用这个做唯一判断,因为反反爬虫非常容易,直接随机UA即可 ...

  3. 大众点评评论数据抓取 反爬虫措施有css文字映射和字体库反爬虫

    大众点评评论数据抓取  反爬虫措施有css文字映射和字体库反爬虫 大众点评的反爬虫手段有那些: 封ip,封账号,字体库反爬虫,css文字映射,图形滑动验证码 这个图片是滑动验证码,访问频率高的话,会出 ...

  4. WebSocket 反爬虫

    目录 WebSocket握手验证反爬虫 WebSocket 消息校验反爬虫 WebSocket Ping 反爬虫 总结 WebSocket握手验证反爬虫 ! HTTP协议 请求头 服务器端创建 soc ...

  5. 自动更改IP地址反爬虫封锁，支持多线程(转)

    8年多爬虫经验的人告诉你,国内ADSL是王道,多申请些线路,分布在多个不同的电信机房,能跨省跨市更好,我这里写好的断线重拨组件,你可以直接使用. ADSL拨号上网使用动态IP地址,每一次拨号得到的IP ...

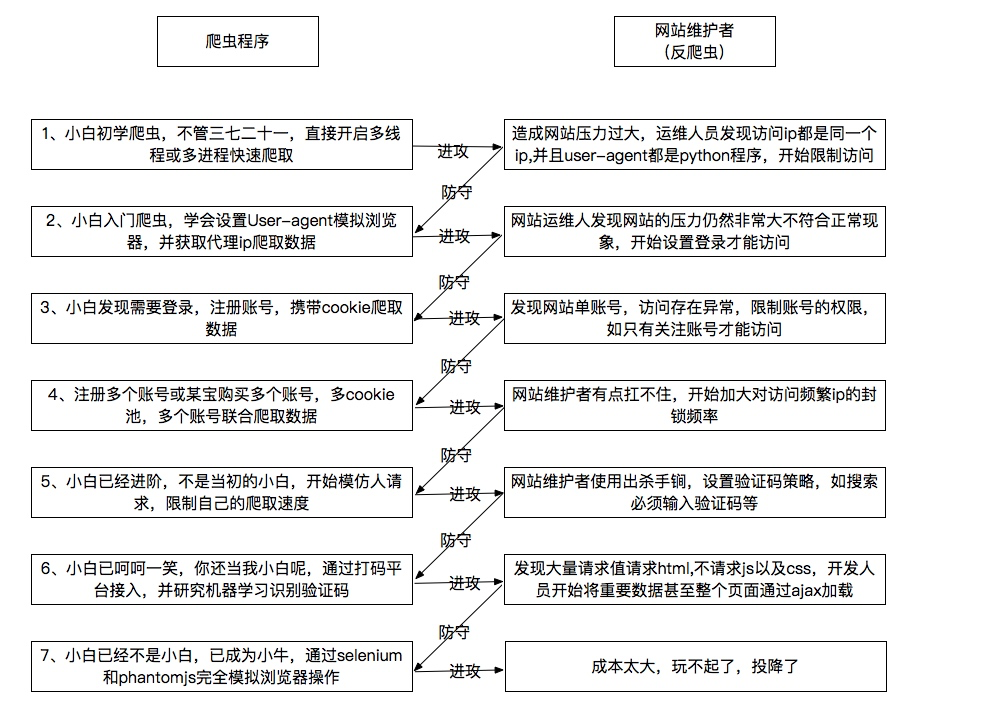
  6. 爬虫(Spider)，反爬虫(Anti-Spider)，反反爬虫(Anti-Anti-Spider)

    爬虫(Spider),反爬虫(Anti-Spider),反反爬虫(Anti-Anti-Spider),这之间的斗争恢宏壮阔... Day 1小莫想要某站上所有的电影,写了标准的爬虫(基于HttpCli ...

  7. Python Scrapy反爬虫常见解决方案（包含5种方法）

    爬虫的本质就是“抓取”第二方网站中有价值的数据,因此,每个网站都会或多或少地采用一些反爬虫技术来防范爬虫.比如前面介绍的通过 User-Agent 请求头验证是否为浏览器.使用 JavaScript ...

  8. 反爬虫：利用ASP.NET MVC的Filter和缓存（入坑出坑） C#中缓存的使用 C#操作redis WPF 控件库——可拖动选项卡的TabControl 【Bootstrap系列】详解Bootstrap-table AutoFac event 和delegate的分别 常见的异步方式async 和 await C# Task用法 c#源码的执行过程

    反爬虫:利用ASP.NET MVC的Filter和缓存(入坑出坑)   背景介绍: 为了平衡社区成员的贡献和索取,一起帮引入了帮帮币.当用户积分(帮帮点)达到一定数额之后,就会“掉落”一定数量的“帮帮 ...

  9. python3爬虫--反爬虫应对机制

    python3爬虫--反爬虫应对机制 内容来源于: Python3网络爬虫开发实战: 网络爬虫教程(python2): 前言: 反爬虫更多是一种攻防战,针对网站的反爬虫处理来采取对应的应对机制,一般需 ...

随机推荐

  1. Base64 加解密

    import java.io.UnsupportedEncodingException; import org.apache.tomcat.util.codec.binary.Base64; /** ...

  2. bootstrap弹窗、弹出层、modal

    bootstrap弹窗.弹出层.modal 引入bootstrap的js文件    如下div代码 <div class="modal fade" id="myMo ...

  3. 集群环境下的Session共享

    一.Cookie机制和Session机制回顾 1)定义:Session成为“会话”,具体是指一个终端用户与交互系统进行通信的时间间隔,通常指从注册进入系统到注销退出系统之间所经过的时间.Session ...

  4. hdu5701-中位数计数

    题目链接:http://acm.hdu.edu.cn/showproblem.php?pid=5701 题目: Problem Description 中位数定义为所有值从小到大排序后排在正中间的那个 ...

  5. 微信小程序--家庭记账本开发--06

    重要部分学习——记账簿 本次项目开发的目的主要是记账本的开发,最初自己想法简单,把家里的纸质记账簿变成手机上的记账簿.最终自己程序可以实现的功能可以记录每天的账目信息,并形成叠加效果,并按1.2.3… ...

  6. 【软件工程】分布式版本控制系统Git的安装与使用

    作业的要求来自于:https://edu.cnblogs.com/campus/gzcc/GZCC-16SE2/homework/2097 远端库地址:https://github.com/Richa ...

  7. arcgis中转换netCDF为栅格数据

    最近有个同学询问我一个问题,使用arcpy把netcdf转化成栅格文件,忙活了两个小时才搞定,其实主要代码非常简单,只不过要对arcgis 的功能比较熟悉(其实多思考和查考它的帮助文章,无聊) # - ...

  8. c#关键字和常用类型表快查

    类型 字节 取值范围 说明 bool 1 true/false/null 布尔类型 char 2 0x0000~0xffff Unicode 16 位字符 byte 1 0~255 无符号的 8 位整 ...

  9. d4-01

    一.字典 1.1 var dict = {"name":"zhangsan"}  定义字典 1.2 dict.name     取得name的值 1.3 del ...

  10. GMA Round 1 波动函数

    传送门 波动函数 f(x)是一个定义在R上的偶函数,f(x)=f(2-x),当$x\in[-1,1]$时,f(x)=cos(x),则函数$g(x)=f(x)-|cos(\pi x)|$,求g(x)在[ ...