清明培训 清北学堂 DAY2

今天是钟皓曦老师的讲授~~

总结了一下今天的内容：

数论！！！

1.整除性

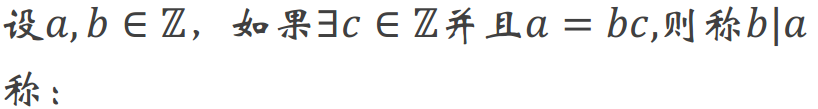
2.质数

定义：

性质：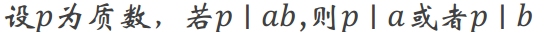 

3.整数分解定理——算数基本定理

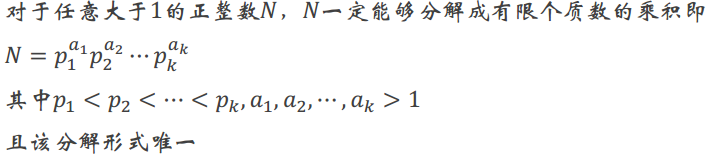
证明：

存在性：

设N是最小不满足唯一分解定理的整数

（1）  若N为质数，则N=N¹，所以N不存在；

（2）  若N为合数，则N=P*（N/P），因为N/P也是不满足定理的整数

所以与N是不满足定理的最小整除相矛盾

所以N不存在

唯一性：

4.素数的判定

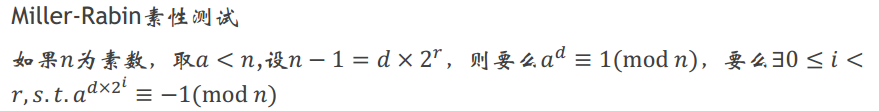（注：s.t.是“使得”的意思）

根据钟神长者的小学经验：取2,3,5,7,13,29,37,89这8个素数在int范围内是100%准的

时间复杂度为O（klogn）

怎么代码实现呢？？？

首先我们要先求出d和r，然后快速幂求出a^d和a^（d*2^i）

a^（d*2^i）当然有别的好方法求啦，看下面：

a^（d*2^（i-1）*2）=（a^（d*2^（i-1）））^2=（（a^（d*2^（i-2）））^2）^2……最后搞下去就变成了a^（d*2^i）

所以我们只要把快速幂后的a^（d*2^i）再进行快速幂就行啦

程序代码：

int gg[8] = {2,3,5,7,13,29,37,89};            //8个好用的素数

bool miller_rabin(int a,int n)                   
{
int d=n-1,r=0;
while (d%2==0)
d/=2,r++;                                                //求d和r
int x = kuaisumi(a,d,n);                          //快速幂a^d
if (x==1) return true;                              //判断a^d%n是否为1，若是，则可能是质数；若否，进行下一层判断
for (int i=0;i<r;i++)
{
if (x==n-1) return true;
x=(long long)x*x%n;                             //将a^d进行快速幂来判断a^（d*2^i）%n是否为-1也就是n-1；
}
return false;
}

bool is_prime(int n)
{
if (n<=1) return false;
for (int a=0;a<8;a++)
if (n==gg[a]) return true;                               //判断n是否为列举的素数中的任何一个，若是则直接判为素数
for (int a=0;a<8;a++)
if (!miller_rabin(gg[a],n)) return false;           //进行miller_rabin素数检查
return true;
}

int kuaisumi（int a,int d,int n） {                  //快速幂函数

int ans=1;

while(b)

{

if(b&1)  ans=ans*a%n;

a=a*a%n;

b>>=1;

}

5.裴蜀定理

设d=gcd（a，b）；

6.扩展欧几里得

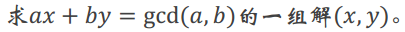
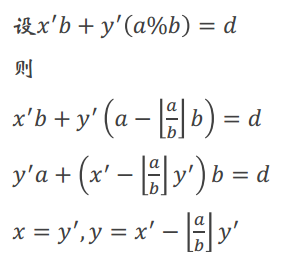
程序代码：

第10行和第4行都是返回的最大公约数，而x，y的值都地址返回了

7.中国剩余定理

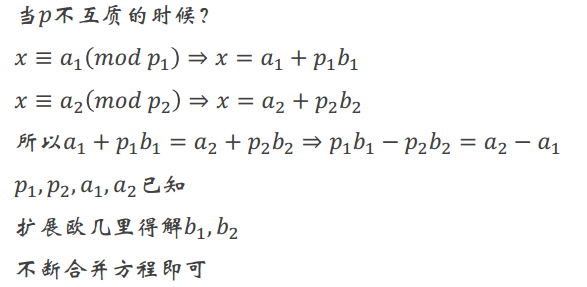
另外我们还可以用大数翻倍法做

8.逆元

定义：

我们都知道欧拉定理：

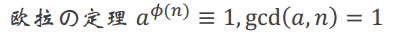
怎么证呢？？？

（1）  

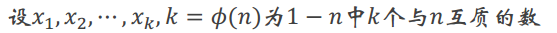
那么都<n且都与n互质

所以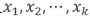对于mod n是不同余的

那么同乘a也是不同余的

那么这其中的任何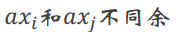

这样我们得到了

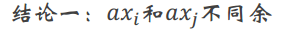
既然这其中的任何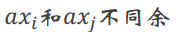，那么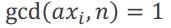

这样我们得到了

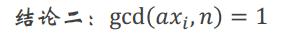
每一个乘a后mod n的余数不变，那么我们可以说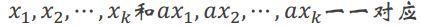

这样我们就得到了

由此我们就可以得到：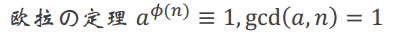

9.Miller_Rabin 二次侦探定理

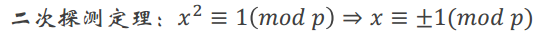
说明一下：     x²≡1 （mod p）

x²-1≡0 （mod p）

（x+1）（x-1）≡0 （mod p）

x≡1或-1

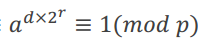
a^（d*2^r）-1≡0 （mod p）

（a^（d*2^（r-1））-1）（a^（d*2^（r-1））+1）≡0 （mod p）

a^（d*2^（r-1））≡1或a^（d*2^（r-1））≡-1

若a^（d*2^（r-1））≡-1，则满足Miller_Rabin的第二个式子，直接判定n为质数

否则a^（d*2^（r-1））≡1

a^（d*2^（r-1））-1≡0 （mod p）

(a^（d*2^（r-2））+1)(a^（d*2^（r-2））-1)≡0 (mod p）

a^（d*2^（r-2））≡1或a^（d*2^（r-2））≡-1

若a^（d*2^（r-2））≡-1，则满足Miller_Rabin的第二个式子，直接判定n为质数

否则a^（d*2^（r-2））≡1

……

10.线性求逆元

程序代码：

int inv[i]=1；

for(int i=2;i<=10;i++)

{

inv[i]=(p-(p/i))*inv[p%i]%p;

}

11.BSGS算法

先来引入积性函数和完全积性函数的概念：

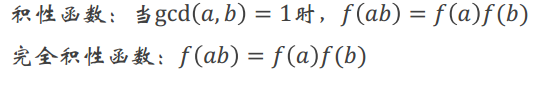
以下是几个常见的积性函数：

可能大家对莫比乌斯函数μ（n）不大熟悉，我来给大家介绍一下：

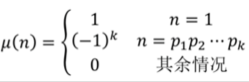
我们来了解一下莫比乌斯函数的性质

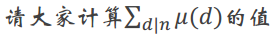
答案很简单：当n=1时，答案为1；当n不为1时，答案为0；

莫比乌斯反演

F(n)和f(n)为算术函数，若他们满足

则有