遗传算法（GA）

来自：https://blog.csdn.net/u010451580/article/details/51178225

　　

遗传算法是模仿生物进化机制的随机全局搜索和优化方法。借鉴达尔文进化论和孟德尔的遗传学说。

相关术语：

　　基因型(genotype)：性状染色体的内部表现；

　　表现形(phenotype)：性状外部表现。或个体的外部表现。

　　进化(evolution)：种群逐渐适应生存环境。生物进化是以种群的形式进行。

　　适应度(fitness)：度量某个物种对生存环境的适应程度。

　　选择(selection)：以一定的概率从种群中选择若干个个体。一般，选择过程是基于适应度的优胜劣汰的过程。

　　复制(reproduction)：细胞分裂时，DNA通过复制转移到新细胞，新细胞继承旧细胞的基因。

　　交叉(crossover)：两个染色体相同位置DNA被切断，前后两串分别交叉组合成两个新染色体。

　　变异(mutation)：复制时小概率产生差错，产生新染色体，表现出新性状。

　　编码(coding)：DNA中遗传信息在一个长链上按一定模式排列。

　　解码(decoding)：基因型到表现型的映射。

　　遗传算法中每条染色体对应遗传算法的一个解决方案，用适应性函数衡量解决方案的优劣。所以从一个基因组到其解的适应度形成一个映射。遗传算法过程可以看作是一个多元函数求最优解的过程。

实例：已知一元函数 f(x) = xsin(10πx)+2   x∈[-1,2]，求函数最大值。

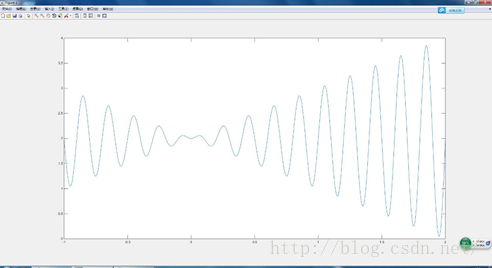
“袋鼠跳”问题

　　函数曲线理解成山峰和山谷的组成，设想得到的每个解就是一只袋鼠，求最大值转换为袋鼠不断的向更高处跳，直到最高的山峰。

爬山法：

　　爬山法中，袋鼠只上坡，没下坡，但不能保证是全局最高峰。

模拟退火：

　　模拟退火中，袋鼠喝醉了，而且随机地大跳很长时间。运气好的话，从一个山峰跳过山谷，到了另外一个更高的山峰上。但最后，它渐渐清醒了并朝着它所在的峰顶跳去。

遗传算法：

　　遗传法中，有很多袋鼠，降落到不同地方，这些袋鼠不知道它们的任务是寻找全局最高峰。但每过几年，就在一些海拔较低的山峰射杀一些袋鼠，并希望存活的袋鼠是多产的，在所处地方生儿育女。最后袋鼠都聚拢到全局最高峰上。

遗传算法实现过程：

• 首先寻找一种对问题潜在解进行“数字化”编码的方案。
• 然后用随机数初始化一个种群（那么第一批袋鼠被随意分散在山上），种群里面的个体就是这些数字化的编码。
• 接下来，通过适当的解码（得到袋鼠的位置坐标），用适应性函数对每个基因个体做一次适应度评估（袋鼠爬的越高，适应度越高）。
• 用选择函数按照某种规定择优选择（每隔一段时间，射杀海拔较低的袋鼠，保持袋鼠总数平衡）。
• 让个体基因变异（让袋鼠随机跳跳）。
• 然后产生子代（希望存活下来的袋鼠多产，在那生儿育女）。

遗传算法并不保证获得问题最优解，它的最大优点在于不必操心如何“找”最优，只是“否定”不好的（把表现不好的，射杀）。

遗传算法一般步骤：

1. 评估每条染色体所对应个体的适应度。
2. 遵照适应度越高，选择概率越大原则，从中群中选择两个个体作为父方和母方。
3. 抽取父母双方的染色体，进行交叉，产生子代。
4. 对子代的染色体进行变异。
5. 重复2,3,4步骤，直到新种群产生。

遗传算法过程的细节：

绘制袋鼠的染色体——基因编码方式

• 采用二进制编码，如：010010011011011110111110
• 采用浮点数编码，如：1.2 –3.3 – 2.0 –5.4 – 2.7 – 4.3
• 采用符号编码。

　　在遗传算法中关心的是袋鼠的位置（海拔低的被射杀），所以以袋鼠的位置作为特征进行编码，具体来说位置就是横坐标。 接着建立表现型到基因型的映射关系。就是如何用编码来变现出袋鼠所在的横坐标。由于横坐标是一个实数，说透了我们就是对这个实数编码。

　　袋鼠的染色体就是横坐标上实数的二进制编码。

物竞天择——适应性评分与选择函数

1.物竞——适应度函数

袋鼠的海拔高度作为它的适应性评分。即适应度函数直接返回函数值就行了。

2.天择——选择函数

常用选择方法——轮盘赌

比如有5条染色体，他们所对应的适应度评分分别为：5，7，10，13，15。

所以累计总适应度为：

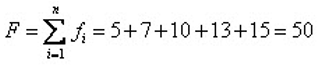
所以各个个体被选中的概率分别为：

注：还有精英选择机制

遗传变异——基因重组（交叉）与基因突变

这两种遗传操作，二进制编码与浮点型编码处理上很大差异。

1. 基因重组、交叉

(1)、二进制编码

类似高中生物中同源染色体的联会过程(随机把其中几个位于同一位置的编码进行交换，产生新的个体。)

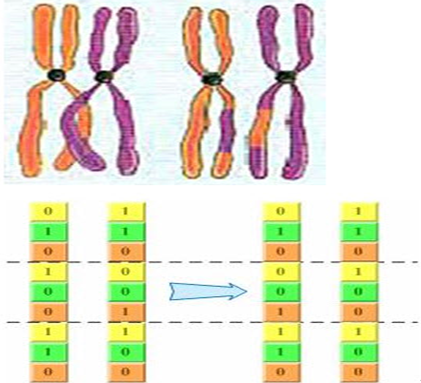
(2)、浮点数编码