[Reinforcement Learning] Value Function Approximation

为什么需要值函数近似？

之前我们提到过各种计算值函数的方法，比如对于 MDP 已知的问题可以使用 Bellman 期望方程求得值函数；对于 MDP 未知的情况，可以通过 MC 以及 TD 方法来获得值函数，为什么需要再进行值函数近似呢？

其实到目前为止，我们介绍的值函数计算方法都是通过查表的方式获取的：

• 表中每一个状态 \(s\) 均对应一个 \(V(s)\)
• 或者每一个状态-动作 <\(s, a\)>

但是对于大型 MDP 问题，上述方法会遇到瓶颈：

• 太多的 MDP 状态、动作需要存储
• 单独计算每一个状态的价值都非常的耗时

因此我们需要有一种能够适用于解决大型 MDP 问题的通用方法，这就是本文介绍的值函数近似方法。即：
\[
\hat{v}(s, \mathbf{w}) \approx v_{\pi}(s) \\
\text{or } \hat{q}(s, a, \mathbf{w}) \approx q_{\pi}(s, a)
\]

那么为什么值函数近似的方法可以求解大型 MDP 问题？

对于大型 MDP 问题而言，我们可以近似认为其所有的状态和动作都被采样和计算是不现实的，那么我们一旦获取了近似的值函数，我们就可以对于那些在历史经验或者采样中没有出现过的状态和动作进行泛化（generalize）。

进行值函数近似的训练方法有很多，比如：

• 线性回归
• 神经网络
• 决策树
• ...

此外，针对 MDP 问题的特点，训练函数必须可以适用于非静态、非独立同分布（non-i.i.d）的数据。

增量方法

梯度下降

梯度下降不再赘述，感兴趣的可以参考之前的博文《梯度下降法的三种形式BGD、SGD以及MBGD》

通过随机梯度下降进行值函数近似

我们优化的目标函数是找到一组参数 \(\mathbf{w}\) 来最小化最小平方误差（MSE），即：
\[J(\mathbf{w}) = E_{\pi}[(v_{\pi}(S) - \hat{v}(S, \mathbf{w}))^2]\]

通过梯度下降方法来寻优：
\[
\begin{align}
\Delta\mathbf{w}
&=-\frac{1}{2}\alpha\triangledown_{\mathbf{w}}J(\mathbf{w})\\
&=\alpha E_{\pi}\Bigl[\Bigl(v_{\pi}(S) - \hat{v}(S, \mathbf{w})\Bigr)\triangledown_{\mathbf{w}}J(\mathbf{w})\Bigr]
\end{align}
\]

对于随机梯度下降（Stochastic Gradient Descent，SGD），对应的梯度：
\[\Delta\mathbf{w} = \alpha\underbrace{\Bigl(v_{\pi}(S) - \hat{v}(S, \mathbf{w})\Bigr)}_{\text{error}}\underbrace{\triangledown_{\mathbf{w}}\hat{v}(S, \mathbf{w})}_{\text{gradient}}\]

值函数近似

上述公式中需要真实的策略价值函数 \(v_{\pi}(S)\) 作为学习的目标（supervisor），但是在RL中没有真实的策略价值函数，只有rewards。在实际应用中，我们用target来代替 \(v_{\pi}(S)\)：

• 对于MC，target 为 return \(G_t\)：
  \[\Delta\mathbf{w}=\alpha\Bigl(G_t - \hat{v}(S_t, \mathbf{w})\Bigr)\triangledown_{\mathbf{w}}\hat{v}(S_t, \mathbf{w})\]
• 对于TD(0)，target 为TD target \(R_{t+1}+\gamma\hat{v}(S_{t+1}, \mathbf{w})\)：
  \[\Delta\mathbf{w}=\alpha\Bigl(R_{t+1} + \gamma\hat{v}(S_{t+1}, \mathbf{w})- \hat{v}(S_t, \mathbf{w})\Bigr)\triangledown_{\mathbf{w}}\hat{v}(S_t, \mathbf{w})\]
• 对于TD(λ)，target 为 TD λ-return \(G_t^{\lambda}\)：
  \[\Delta\mathbf{w}=\alpha\Bigl(G_t^{\lambda}- \hat{v}(S_t, \mathbf{w})\Bigr)\triangledown_{\mathbf{w}}\hat{v}(S_t, \mathbf{w})\]

在获取了值函数近似后就可以进行控制了，具体示意图如下：

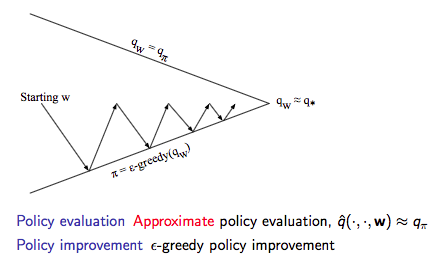
动作价值函数近似

动作价值函数近似：
\[\hat{q}(S, A, \mathbf{w})\approx q_{\pi}(S, A)\]

优化目标：最小化MSE
\[J(\mathbf{w}) = E_{\pi}[(q_{\pi}(S, A) - \hat{q}(S, A, \mathbf{w}))^2]\]

使用SGD寻优：
\[\begin{align}
\Delta\mathbf{w}
&=-\frac{1}{2}\alpha\triangledown_{\mathbf{w}}J(\mathbf{w})\\
&=\alpha\Bigl(q_{\pi}(S, A)-\hat{q}_{\pi}(S, A, \mathbf{w})\Bigr) \triangledown_{\mathbf{w}}\hat{q}_{\pi}(S, A, \mathbf{w})
\end{align}\]

收敛性分析

略，感兴趣的可以参考David的课件。

批量方法

随机梯度下降SGD简单，但是批量的方法可以根据agent的经验来更好的拟合价值函数。

值函数近似

优化目标：批量方法解决的问题同样是 \(\hat{v}(s, \mathbf{w})\approx v_{\pi}(s)\)

经验集合 \(D\) 包含了一系列的 <state, value> pair：
\[D=\{<s_1, v_1^{\pi}>, <s_2, v_2^{\pi}>, ..., <s_T, v_T^{\pi}>\}\]

根据最小化平方误差之和来拟合 \(\hat{v}(s, \mathbf{w})\) 和 \(v_{\pi}(s)\)，即：
\[
\begin{align}
LS(w)
&= \sum_{t=1}^{T}(v_{t}^{\pi}-\hat{v}(s_t, \mathbf{w}))^2\\
&= E_{D}[(v^{\pi}-\hat{v}(s, \mathbf{w}))^2]
\end{align}
\]

经验回放（Experience Replay）：

给定经验集合：
\[D=\{<s_1, v_1^{\pi}>, <s_2, v_2^{\pi}>, ..., <s_T, v_T^{\pi}>\}\]
Repeat：

1. 从经验集合中采样状态和价值：\(<s, v^{\pi}>\sim D\)
2. 使用SGD进行更新：\(\Delta\mathbf{w}=\alpha\Bigl(v^{\pi}-\hat{v}(s, \mathbf{w})\Bigr)\triangledown_{\mathbf{w}}\hat{v}(s, \mathbf{w})\)
   通过上述经验回放，获得最小化平方误差的参数值：
   \[\mathbf{w}^{\pi}=\arg\min_{\mathbf{w}}LS(\mathbf{w})\]

我们经常听到的 DQN 算法就使用了经验回放的手段，这个后续会在《深度强化学习》中整理。

通过上述经验回放和不断的迭代可以获取最小平方误差的参数值，然后就可以通过 greedy 的策略进行策略提升，具体如下图所示：

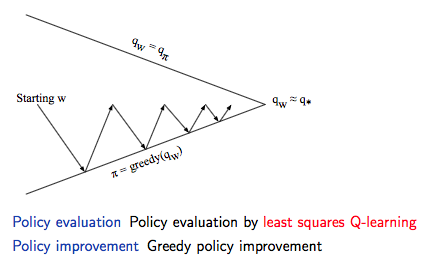
动作价值函数近似

同样的套路：

• 优化目标：\(\hat{q}(s, a, \mathbf{w})\approx q_{\pi}(s, a)\)
• 采取包含 <state, action, value> 的经验集合 \(D\)
• 通过最小化平方误差来拟合

对于控制环节，我们采取与Q-Learning一样的思路：

• 利用之前策略的经验
• 但是考虑另一个后继动作 \(A'=\pi_{\text{new}}(S_{t+1})\)
• 朝着另一个后继动作的方向去更新 \(\hat{q}(S_t, A_t, \mathbf{w})\)，即
  \[\delta = R_{t+1} + \gamma\hat{q}(S_{t+1}, \pi{S_{t+1}, \mathbf{\pi}}) - \hat{q}(S_t, A_t, \mathbf{w})\]
• 梯度：线性拟合情况，\(\Delta\mathbf{w}=\alpha\delta\mathbf{x}(S_t, A_t)\)

收敛性分析

略，感兴趣的可以参考David的课件。

Reference

[1] Reinforcement Learning: An Introduction, Richard S. Sutton and Andrew G. Barto, 2018
[2] David Silver's Homepage