FPGA之CORDIC算法实现_理论篇(上）

关于cordic的算法原理核心思想就是规定好旋转角度，然后通过不停迭代逐步逼近的思想来实现数学求解，网上关于这部分的资料非常多，主要可以参考：

1）https://blog.csdn.net/qq_39210023/article/details/77456031

2）https://blog.csdn.net/rookiew/article/details/74967394

Xinlinx自带的官方说明文档也非常值得参考，文章末尾会补充相关参考资料。

1、cordic的优化算法：

1）

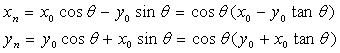
2）第一次旋转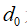，为旋转方向

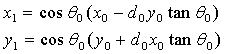
3）第二次旋转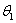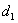，为旋转方向

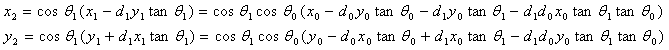
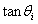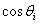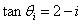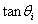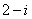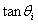式子一直都会有和，每次都可以提取。虽然FPGA无法计算，但，因此可以执行和效果相同的移位操作来取代。对于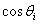，可以预先全部提取出来，然后等待迭代结束之后，再把因为简化计算过程抽出的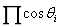还原回去即可。

2、公式总结：

提取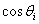，2-i等效替换成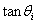

1）

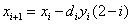
2）

3）

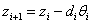
迭代过程：

i从0开始迭代，假设当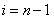时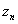，趋向于0(i从0至n-1)，得到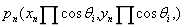点，此时点就近似等于之前假设的点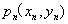，此时将之前抽出的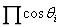还原回去。

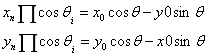
进一步将式子转化，可得

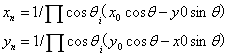
注意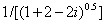：，的极值为1，因此当i的次数很大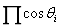，的值趋于一个常数。

3、求解sina，cosa的起点取值问题

设起点（x0，y0），当i = n-1时，迭代结束，到达终点（xn, yn),  因为中间用了伪旋转，所以结果必须要乘以为了简化计算过程抽出的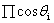，因此有

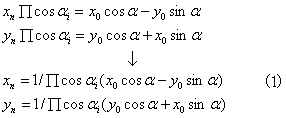
观察上面的式子，我们的目标是根据迭代后的xn、yn求出sina，cosa，因此可设

可将（1）化简得到

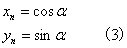
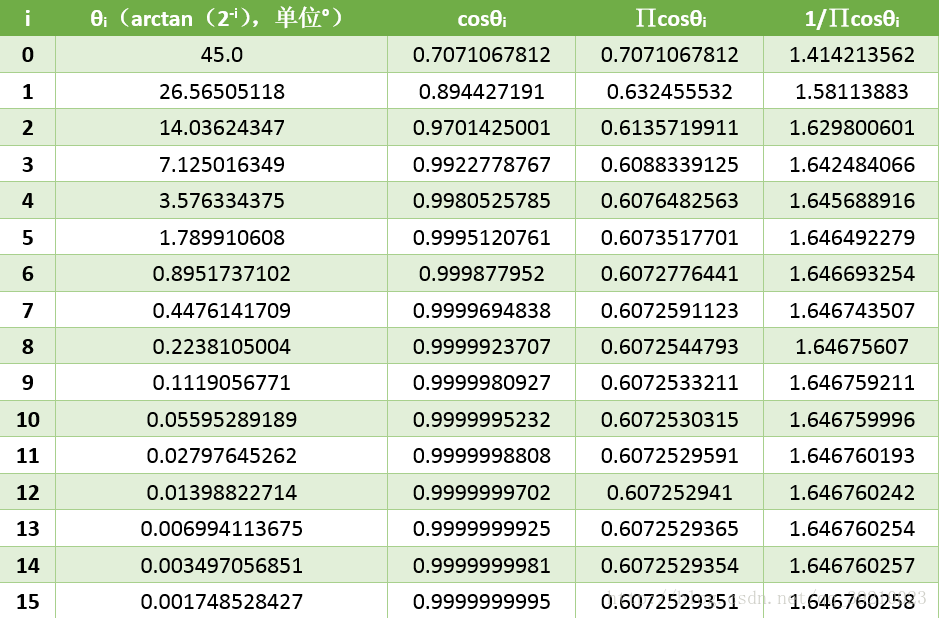
上式中的xn，yn是经过迭代后的结果，而不是之前一开始假设的点（xn，yn），要注意区分这一点。因此，我们可以观察到，最后正余弦的求解仅仅是以初始点的设置以及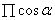的值有关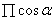，可以预先通过matlab求解预存起来，一般经过16次的迭代后就逐渐趋于稳定。

下一篇，我会接着来讲用FPGA来实现这个Cordic算法。