hihocoder #1388 : Periodic Signal fft

题目链接：

https://hihocoder.com/problemset/problem/1388

Periodic Signal

时间限制:5000ms
内存限制:256MB
#### 问题描述
> Profess X is an expert in signal processing. He has a device which can send a particular 1 second signal repeatedly. The signal is A0 ... An-1 under n Hz sampling.
>
> One day, the device fell on the ground accidentally. Profess X wanted to check whether the device can still work properly. So he ran another n Hz sampling to the fallen device and got B0 ... Bn-1.
>
> To compare two periodic signals, Profess X define the DIFFERENCE of signal A and B as follow:
>
>
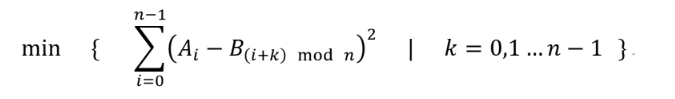
> You may assume that two signals are the same if their DIFFERENCE is small enough.
> Profess X is too busy to calculate this value. So the calculation is on you.
#### 输入
> The first line contains a single integer T, indicating the number of test cases.
>
> In each test case, the first line contains an integer n. The second line contains n integers, A0 ... An-1. The third line contains n integers, B0 ... Bn-1.
>
> T≤40 including several small test cases and no more than 4 large test cases.
>
> For small test cases, 0
> For large test cases, 0
> For all test cases, 0≤Ai,Bi For each test case, print the answer in a single line.
####样例输入
> 2
> 9
> 3 0 1 4 1 5 9 2 6
> 5 3 5 8 9 7 9 3 2
> 5
> 1 2 3 4 5
> 2 3 4 5 1

样例输出

80

0

题意

给你两个大小为n的数组a,b，求：

题解

构造下a，b数组就可以转换成多项式乘法问题，然后用fft计算，注意最后计算结果会有浮点误差，但是大小关系还是可以用的，所以求出最大的位置之后，把答案再算一遍。

构造：

另n等于3：

a0a1a2 --> a2a1a0

b0b1b2 --> b0b1b2b0b1b2

这样x^2到x4的系数就是答案。

代码

#include<algorithm>
#include<iostream>
#include<cstdio>
#include<cmath>
using namespace std;
#define scf scanf
#define prf printf

const int maxn=24e4+10;
const double PI=acos(-1.0);
const double eps=1e-8;
typedef long long LL;

struct Complex {
    double real, image;
    Complex(double real, double image):real(real),image(image) {}
    Complex() {}
    friend Complex operator + (const Complex &c1, const Complex &c2) {
        return Complex(c1.real + c2.real, c1.image + c2.image);
    }
    friend Complex operator - (const Complex &c1, const Complex &c2) {
        return Complex(c1.real - c2.real, c1.image - c2.image);
    }
    friend Complex operator * (const Complex &c1, const Complex &c2) {
        return Complex(c1.real*c2.real - c1.image*c2.image, c1.real*c2.image + c1.image*c2.real);
    }
}A[maxn],B[maxn];

struct IterativeFFT {
    Complex A[maxn];

    int rev(int id, int len) {
        int ret = 0;
        for(int i = 0; (1 << i) < len; i++) {
            ret <<= 1;
            if(id & (1 << i)) ret |= 1;
        }
        return ret;
    }

    //当DFT= 1时是DFT, DFT = -1则是逆DFT
    //对长度为len(2的幂)的数组进行DFT变换
    void FFT(Complex *a,int len, int DFT) {
        for(int i = 0; i < len; i++)
            A[rev(i, len)] = a[i];
        for(int s = 1; (1 << s) <= len; s++) {
            int m = (1 << s);
            Complex wm = Complex(cos(DFT*2*PI/m), sin(DFT*2*PI/m));
            //这一层结点的包含数组元素个数都是(1 << s)
            for(int k = 0; k < len; k += m) {
                Complex w = Complex(1, 0);
                //折半引理, 根据两个子节点计算父亲节点
                for(int j = 0; j < (m >> 1); j++) {
                    Complex t = w*A[k + j + (m >> 1)];
                    Complex u = A[k + j];
                    A[k + j] = u + t;
                    A[k + j + (m >> 1)] = u - t;
                    w = w*wm;
                }
            }
        }
        if(DFT == -1) for(int i = 0; i < len; i++) A[i].real /= len, A[i].image /= len;
        for(int i=0; i<len; i++) a[i]=A[i];
    }

    int solve(Complex* a,Complex* b,int len,int n){
        FFT(a,len,1),FFT(b,len,1);
        for(int i=0;i<len;i++) a[i]=a[i]*b[i];
        FFT(a,len,-1);

        int pos=0;
        double ans=-1;
        for(int i=0;i<n;i++){
            if(ans+eps<a[i+n-1].real){
                ans=a[i+n-1].real;
                pos=i;
            }
        }
        return pos;
    }

} myfft;

LL a[maxn],b[maxn];
int n;

int main(){
    int tc;
    scf("%d",&tc);
    while(tc--){
        scf("%d",&n);
        int len=1; while(len<n*2) len<<=1;
        for(int i=0;i<n;i++) scf("%lld",&a[i]);
        for(int i=0;i<n;i++) scf("%lld",&b[i]);

        for(int i=0;i<len;i++){
            A[i]=Complex(0,0),B[i]=Complex(0,0);
        }

        for(int i=0;i<n;i++){
            A[i]=Complex(a[n-1-i],0),B[i]=Complex(b[i],0);
            A[i+n]=Complex(0,0), B[i+n]=Complex(b[i],0);
        }

        int k=myfft.solve(A,B,len,n);

        LL ans=0;
        for(int i=0;i<n;i++){
            int j=(i+k)%n;
            ans+=(a[i]-b[j])*(a[i]-b[j]);
        }

        prf("%lld\n",ans);
    }
}