算法导论学习-binary search tree
1. 概念:
Binary-search tree(BST)是一颗二叉树,每个树上的节点都有<=1个父亲节点,ROOT节点没有父亲节点。同时每个树上的节点都有[0,2]个孩子节点(left child AND right child)。每个节点都包含有各自的KEY值以及相应的satellite data。其中KEY是几种BST基本操作的主要操作对象。
2. BST的特别性质:
BST任何一颗子树上的三个节点left, parent, right. 满足条件left.key<parent.key<=right.key,一颗典型的BST如下图所示:
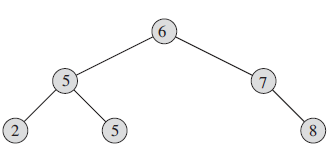
观察之后不难发现如果对BST进行PREORDER walk(先序遍历),得到:2, 5, 5, 6, 7, 8 刚好是升序排列。
P.S 所谓PREORDER walk,就是要访问以ROOT为根的树,先要访问ROOT.left, 然后访问ROOT, 最后访问ROOT.right。
用pseudocode的形式的话,就是这样:
PREORDER-WALK(x) 1 if(x!=NIL) 2 PREORDER-WALK(x.left) 3 print x.key 4 PREORDER-WALK(x.right)
3. BST的几种基本操作:
SEARCH, MINIMUM, MAXIMUM, PREDECESSOR, SUCCESSOR, INSERT, and DELETE.
2.1 SEARCH:
TREE-SEARCH(x, k)
INPUT: BST ROOT node, value k.
OUPUT: node in BST whose key equals to k
1 if(x==NIL) OR (k==x.key)
2 return x
3 if(k<x.key)
4 return TREE-SEARCH(x.left, k)
5 else return TREE-SEARCH(x.right, k)
算法解释:当我们要找到key值为k的节点在BST中的位置,我们一般调用上述函数TREE-SEARCH(ROOT, k)(ROOT为BST的根节点)。如果ROOT节点的key值等于k,则我们要找的节点就是根节点ROOT。如果不是,根据BST的特殊性质:
left.key<parent.key<=right.key
我们比较当前节点的key值,如果current.key<k,则要在当前节点的左子树中查找,反之,则在右子树中查找。[line3-line5]
2.2 MINIMUM:
TREE-MINIMUM(x)
INPUT: BST ROOT node
OUTPUT: the smallest key in BST
1 if(x==NIL) return;
2 while(x.left!=NIL)
3 x=x.left
4 return x.key
算法解释:一个BST的最左叶子节点的key值就是BST所有key值中最小的。这个根据BST的特殊性质很容易推导出来:
因为 left.key < parent.key < parent.key < .... < root.key
有了MINIMUM算法,MAXIMUM算法也就有了:
2.3 MAXIMUM:
TREE-MAXIMUM(x)
INPUT: BST ROOT node
OUTPUT: the smallest key in BST
1 if(x==NIL) return;
2 while(x.right!=NIL)
3 x=x.right
4 return x.key
2.4 SUCCESSOR:
TREE-SUCCESSOR(x)
INPUT: arbitray node x in BST
OUTPUT: x's successor node
1 if(x.right!=NIL)
2 TREE-MINIMUM(x.right)
3 y=x.parent
4 while(y!=NIL AND y.left==x)
5 x=y
6 y=y.parent
7 return y
这里说明一下SUCCESSOR的含义,x的SUCCESSOR满足x.key<=x.SUCCESSOR.key,并且x.SUCCESSOR.key是距离x.key最近的值,即x.SUCCESSOR.key是x.key的最小上限(minimum ceiling)
算法思想:因为在BST中,有x.key<=x.right.key。所以如果某BST的节点x有右孩子节点(x.right!=NIL),则利用TREE-MINIMUM在x的右子树中查找即可。如果x不存在右孩子,则检查x是否有父亲节点并且x必须是父亲节点的左孩子,只有这样才有parent.key>parent.left.key。但找到x的parent就结束了吗,还没有,就像TREE-MINIMUM函数一样,我们需要逐层查找,当找到符合条件的parent后,我们递归的继续检查parent节点有没有parent.parent节点符不符合上述条件。知道访问到的parent节点不符合该条件为止。
2.5 INSERT:
TREE-INSERT(T, z)
1 y=NIL
2 x=T.ROOT
3 while(x!=NIL)
4 y=x
5 if(z.key<x.key)
6 x=x.left
7 else x=x.right
8 z.p=y
9 if(y==NIL) T.ROOT=z
10 if(z.key<y.key) y.left=z
11 else y.right=z
用一张图来解释该算法:
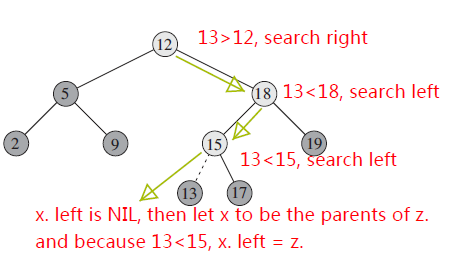
虚线指向的key值为13的节点是即将要插入BST的点,其他的点已经在BST上。可以看到从ROOT节点出发,根据“左小右大”规则,我们很快找到了key值为15的节点,因为13<15,所以检查‘15’节点是否有左孩子,结果是没有,所以把13放到15的左孩子节点处。我们可以想象如果要插入的节点key是16会怎么样?同样的,我们还是找到‘15’节点,但是16>15,所以继续往‘右’查找,找到‘17’,因为16<17,看17有没有左孩子节点,没有,所以会把‘16’放到‘17’的左孩子节点处。
2.6 TRANSPLANT:
TRANPLANT(T, u, v)
1 if (u.parent==NIL) T.ROOT=v
2 else if(u==u.parent;.left) u.parent.left=v
3 else u.parent.right=v
4 if(v!=NIL) v.parent=u.parent
还是用一张图来展示比较清晰:
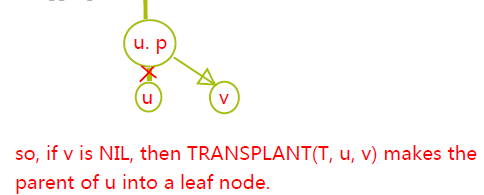
2.7 DELETE:
TREE-DELETE(T, z)
1 if z.left==NIL
2 TRANSPLANT(T, z, z.right)
3 else if z.right == NIL
4 TRANSPLANT(T, z, z.left)
5 else y=TREE-MINIMUM(z.right)
6 if y.parent!=z
7 TRANSPLANT(T, y, y.right)
8 y.right=z.right
9 y.right.parent=y
10 TRANSPLANT(T, z, y)
11 y.left=z.left
12 y.left.parent=y
DELETE算法相对来说比较麻烦一些,需要考虑的情况要多一些。因为要在删除BST的某一节点后仍能维持BST的基本性质。假设要删除的节点是z,z的key值为k。根据“左小右大”原则,z.left.key<k<=z.right.key.如果这时候吧z删了,谁来接替z的位置呢并且保证解体之后的新BST满足性质呢?方法我们可以根据性质来推导:我们要找到一个除了z以外的节点在BST中,该节点假设为P,那么P.key要大于z.left.key并且P.key>=z.right.key,实际上很明显的,唯一符合要求的就是z的SUCCESSOR。
如果z只有左子树或者只有右子树,那么问题就很简单,使z的左孩子或者右孩子来顶替z的位置即可。如果z的左子树和右子树都存在,那么问题稍微复杂一点,我们要在BST上找到z的SUCCESSOR。如此一来,这个问题又变成我们之前讨论的SUCCESSOR问题了,总共有两种情形:
第一种情形:z的右孩子就是我们要找的z的SUCCESSOR,那我们就直接TRANSPLANT移植以z.right为根的子树到z的位置中去。
第二种情形:z的右孩子不是我们要找的z的SUCCESSOR,那我们就从z.right出发,‘深入’寻找知道找到z的SUCCESSOR,假设为Q。
那么我们让Q成为z.right的父亲节点,并且让以Q为根的右子树(因为是根据“最左原则”找到的Q,Q要么是以z.right为根的left-most叶子节点,要么Q只有右子树。)取代Q的位置。最后让Q取代z的位置。。。很绕。。。还是见图吧。
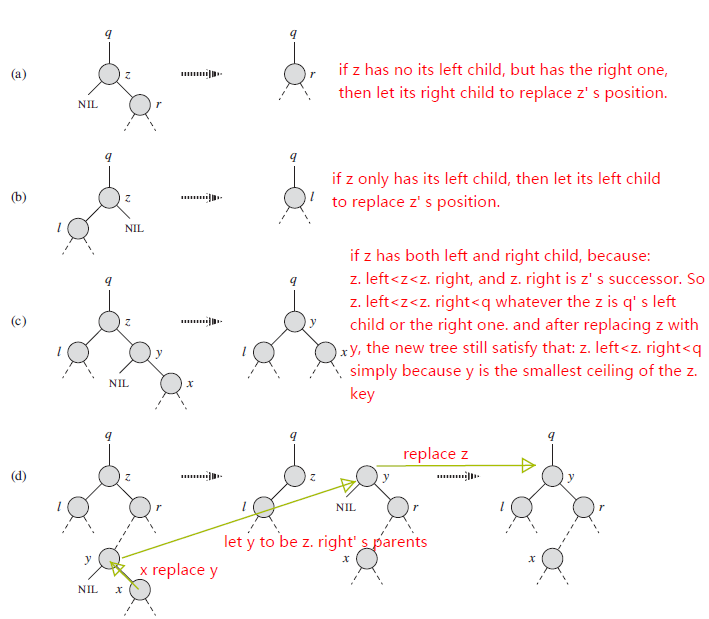
算法导论学习-binary search tree的更多相关文章
- [数据结构]——二叉树(Binary Tree)、二叉搜索树(Binary Search Tree)及其衍生算法
二叉树(Binary Tree)是最简单的树形数据结构,然而却十分精妙.其衍生出各种算法,以致于占据了数据结构的半壁江山.STL中大名顶顶的关联容器--集合(set).映射(map)便是使用二叉树实现 ...
- 72【leetcode】经典算法- Lowest Common Ancestor of a Binary Search Tree(lct of bst)
题目描述: 一个二叉搜索树,给定两个节点a,b,求最小的公共祖先 _______6______ / \ ___2__ ___8__ / \ / \ 0 _4 7 9 / \ 3 5 例如: 2,8 - ...
- 【LeetCode-面试算法经典-Java实现】【109-Convert Sorted List to Binary Search Tree(排序链表转换成二叉排序树)】
[109-Convert Sorted List to Binary Search Tree(排序链表转换成二叉排序树)] [LeetCode-面试算法经典-Java实现][全部题目文件夹索引] 原题 ...
- 笔试算法题(58):二分查找树性能分析(Binary Search Tree Performance Analysis)
议题:二分查找树性能分析(Binary Search Tree Performance Analysis) 分析: 二叉搜索树(Binary Search Tree,BST)是一颗典型的二叉树,同时任 ...
- 将百分制转换为5分制的算法 Binary Search Tree ordered binary tree sorted binary tree Huffman Tree
1.二叉搜索树:去一个陌生的城市问路到目的地: for each node, all elements in its left subtree are less-or-equal to the nod ...
- 编程算法 - 二叉搜索树(binary search tree) 代码(C)
二叉搜索树(binary search tree) 代码(C) 本文地址: http://blog.csdn.net/caroline_wendy 二叉搜索树(binary search tree)能 ...
- 算法与数据结构基础 - 二叉查找树(Binary Search Tree)
二叉查找树基础 二叉查找树(BST)满足这样的性质,或是一颗空树:或左子树节点值小于根节点值.右子树节点值大于根节点值,左右子树也分别满足这个性质. 利用这个性质,可以迭代(iterative)或递归 ...
- 二叉查找树(binary search tree)详解
二叉查找树(Binary Search Tree),也称二叉排序树(binary sorted tree),是指一棵空树或者具有下列性质的二叉树: 若任意节点的左子树不空,则左子树上所有结点的值均小于 ...
- [Data Structure] 二叉搜索树(Binary Search Tree) - 笔记
1. 二叉搜索树,可以用作字典,或者优先队列. 2. 根节点 root 是树结构里面唯一一个其父节点为空的节点. 3. 二叉树搜索树的属性: 假设 x 是二叉搜索树的一个节点.如果 y 是 x 左子树 ...
随机推荐
- Popen No such file or directory 错误
File , in reload_config stderr=PIPE, env={"PATH": '', "HOME": "/root"} ...
- sublime c++ builder
rt, mark { "cmd": ["g++", "${file}", "-o", "${file_path ...
- T[]与List<T>的使用时机
所有的数组类型都隐式地从System.Array这个抽象类派生,而System.Array又派生自System.Object.也就是说数组是引用类型.通过如下方式创建数组: int[] arrInt ...
- linux下修改IP信息
在Linux的系统下如何才能修改IP信息 以前总是用ifconfig修改,重启后总是得重做.如果修改配置文件,就不用那么麻烦了- A.修改ip地址 即时生效: # ifconfig eth0 192. ...
- EL四大作用域 9个jsp对象有效范围 及 对应的类
java中request,session,application的作用范围 page,request,session,application四者的作用范围: page的作用范围是当前页面:对应El表达 ...
- 解决Linux/aix 下的websphere log4j不生效
websphere 解决Linux/aix下的log4j不生效 在目录: /IBM/WebSphere/AppServer/profiles/AppSrv01/properties 增加一个文件:可以 ...
- 1003: [ZJOI2006]物流运输trans
spfa+dp; 刚刚开始一直想不通怎么判断他是否换了道: 后来才知道,将那个时间段打包,找出这段时间内的最短路: 真是太奇妙了! #include<cstdio> #include< ...
- Java 单链表逆序
代码: package com.wangzhu.linkedlist; public class LinkedListDemo { /** * @param args */ public static ...
- Ci框架整合smarty模板引擎
Ci框架整合smarty模板引擎 备注:下载smarty时,最好选择2.6版本,其他测试有坑,ci可以是2.2或其他 大体思路:将smarty封装成ci框架的一个类,然后重新配置一下smarty,这样 ...
- 手势识别官方教程(6)识别拖拽手势用GestureDetector.SimpleOnGestureListener和onTouchEvent
三种现实drag方式 1,在3.0以后可以直接用 View.OnDragListener (在onTouchEvent中调用某个view的startDrag()) 2,onTouchEvent() ...
