Gate Of Babylon bzoj 1272

Gate Of Babylon

【问题描述】

【输入格式】

【输出格式】

【样例输入】

2 1 10 13

3

【样例输出】

12

【样例说明】

【数据范围】

---

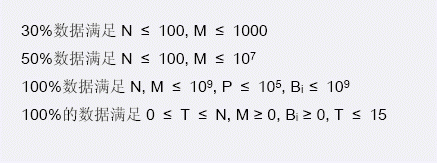
题解：

答案为全部没有限制的方案-有一个超过限制的方案数+有两个超过限制的方案数-有三个超过限制的方案数······

解释一下：

我们先算出所有的方案数，减去每一种超级神器超过限制的方案

而这其中有同时两种神器都都不满足条件的方案

这种方案被减了两次

那么加上有两个超过限制的方案数

有两个超过限制的方案数中有三种同时超过限制的方案数

并且有一种超过限制的方案数中又含有了有三种同时超过的方案数

那么再减去有三种超过限制的方案数

接下来同理······

我们发现答案式子中有奇数个超过限制的方案数为减法，而有偶数个超过限制的方案数为加法

考虑直接Dfs

n组无限制的数中选m个的方案数：C(n+m-1,m)

那么不超过m个的方案数为：C(n+0-1,0)+C(n+1-1,1)+C(n+2-1,2)+···+C(n+m-1,m)=C(n+m,m) (C(n,m)=C(n-1,m-1)+C(n-1,m))

Lucas定理：C(n,m)%p=C(n/p,m/p)*C(n%p,m%p)%p

 #include<algorithm>
 #include<iostream>
 #include<cstring>
 #include<cstdlib>
 #include<cstdio>
 #include<cmath>
 using namespace std;
 long long n, m, t, p;
 inline int Get()
 {
     int x = ;
     char c = getchar();
     while('' > c || c > '') c = getchar();
     while('' <= c && c <= '')
     {
         x = (x << ) + (x << ) + c - '';
         c = getchar();
     }
     return x;
 }
 inline long long Pow(long long m, long long n)
 {
     long long res = ;
     long long sum = m;
     while(n)
     {
         if(n & ) res = (res * sum) % p;
         sum = (sum % p * sum % p) % p;
         n >>= ;
     }
     return res;
 }
 long long ans;
 long long c[];
 long long su[];
 inline long long Zhs(long long a, long long b)
 {
     if(a < b) return ;
     return ((su[a] % p) * Pow((su[b] % p) * (su[a - b] % p) % p, p - )) % p;
 }
 inline long long Lu(long long a, long long b)
 {
     if(a < b) return ;
     long long res = ;
     while(a && b)
     {
         res = (res * Zhs(a % p, b % p)) % p;
         a /= p;
         b /= p;
     }
     return res;
 }
 void Dfs(int x, long long o, long long w)
 {
     if(x == t + )
     {
         ans = ((ans + o * (Lu(m + n - w, m - w) % p)) % p + p) % p;
         return;
     }
     Dfs(x + , o, w);
     Dfs(x + , -o, w + c[x] + );
 }
 int main()
 {
     n = Get(), t = Get(), m = Get(), p = Get();
     for(int i = ; i <= t; ++i) c[i] = Get();
     su[] = ;
     for(int i = ; i <= p; ++i) su[i] = (su[i - ] * i) % p;
     Dfs(, , );
     printf("%lld", ans);
 }