Algorithm --> 最长公共子序列(LCS)
<1> 枚举法
这种方法是最简单,也是最容易想到的,当然时间复杂度也是龟速的,我们可以分析一下,刚才也说过了cnblogs的子序列个数有27个 ,延伸一下:一个长度为N的字符串,其子序列有2N个,每个子序列要在第二个长度为N的字符串中去匹配,匹配一次需要O(N)的时间,总共也就是O(N*2N),可以看出,时间复杂度为指数级,恐怖的令人窒息。
<2> 动态规划
最长公共子序列的结构有如下表示:

代码:
//只能打印一个最长公共子序列
#include <iostream>
using namespace std; const int X = , Y = ; //串的最大长度
char result[X+]; //用于保存结果
int count=; //用于保存公共最长公共子串的个数 /*功能:计算最优值
*参数:
* x:字符串x
* y:字符串y
* b:标志数组
* xlen:字符串x的长度
* ylen:字符串y的长度
*返回值:最长公共子序列的长度
*
*/
int Lcs_Length(string x, string y, int b[][Y+],int xlen,int ylen)
{
int i = ;
int j = ; int c[X+][Y+];
for (i = ; i<=xlen; i++)
{
c[i][]=;
}
for (i = ; i <= ylen; i++ )
{
c[][i]=;
}
for (i = ; i <= xlen; i++)
{
for (j = ; j <= ylen; j++)
{
if (x[i - ] == y[j - ])
{
c[i][j] = c[i-][j-]+;
b[i][j] = ;
}
else if (c[i-][j] > c[i][j-])
{
c[i][j] = c[i-][j];
b[i][j] = ;
}
else if(c[i-][j] <= c[i][j-])
{
c[i][j] = c[i][j-];
b[i][j] = ;
}
}
}
return c[xlen][ylen];
} void Display_Lcs(int i, int j, string x, int b[][Y+],int current_Len)
{
if (i == || j==)
{
return;
}
if(b[i][j]== )
{
current_Len--;
result[current_Len]=x[i- ];
Display_Lcs(i-, j-, x, b, current_Len);
}
else if(b[i][j] == )
{
Display_Lcs(i-, j, x, b, current_Len);
}
else if(b[i][j]==)
{
Display_Lcs(i, j-, x, b, current_Len);
}
else
{
Display_Lcs(i-,j,x,b, current_Len);
}
} int main(int argc, char* argv[])
{
string x = "ABCBDAB";
string y = "BDCABA";
int xlen = x.length();
int ylen = y.length(); int b[X + ][Y + ]; int lcs_max_len = Lcs_Length( x, y, b, xlen,ylen );
cout << lcs_max_len << endl; Display_Lcs( xlen, ylen, x, b, lcs_max_len ); //打印结果如下所示
for(int i = ; i < lcs_max_len; i++)
{
cout << result[i];
}
cout << endl;
return ;
}
运行结果如下:
BDAB
由于有时并不是只有一个最长公共子序列,所以,对上面的代码进行改进,增加一个数组保存结果等....代码如下所示。
//求取所有的最长公共子序列
#include <iostream>
using namespace std; const int X = , Y = ; //串的最大长度
char result[X+]; //用于保存结果
int cnt = ; //用于保存公共最长公共子串的个数 /*功能:计算最优值
*参数:
* x:字符串x
* y:字符串y
* b:标志数组
* xlen:字符串x的长度
* ylen:字符串y的长度
*返回值:最长公共子序列的长度
*
*/
int Lcs_Length(string x, string y, int b[][Y+],int xlen,int ylen)
{
int i = ;
int j = ; int c[X+][Y+];
for (i = ; i<=xlen; i++)
{
c[i][]=;
}
for (i = ; i <= ylen; i++ )
{
c[][i]=;
}
for (i = ; i <= xlen; i++)
{ for (j = ; j <= ylen; j++)
{
if (x[i - ] == y[j - ])
{
c[i][j] = c[i-][j-]+;
b[i][j] = ;
}
else if (c[i-][j] > c[i][j-])
{
c[i][j] = c[i-][j];
b[i][j] = ;
}
else if(c[i-][j] < c[i][j-])
{
c[i][j] = c[i][j-];
b[i][j] = ;
}
else
{
c[i][j] = c[i][j-]; //或者c[i][j]=c[i-1][j];
b[i][j] = ;
}
}
}
return c[xlen][ylen];
} /*功能:计算最长公共子序列
*参数:
* xlen:字符串x的长度
* ylen:字符串y的长度
* x :字符串x
* b:标志数组
* current_len:当前长度
* lcs_max_len:最长公共子序列长度
*
*/
void Display_Lcs(int i, int j, string x, int b[][Y+],int current_len,int lcs_max_len)
{
if (i == || j==)
{
for(int s=; s < lcs_max_len; s++)
{
cout << result[s];
}
cout<<endl;
cnt++;
return;
}
if(b[i][j]== )
{
current_len--;
result[current_len]=x[i- ];
Display_Lcs(i-, j-, x, b,current_len,lcs_max_len);
}
else if(b[i][j] == )
{
Display_Lcs(i-, j, x, b,current_len,lcs_max_len);
}
else if(b[i][j]==)
{
Display_Lcs(i, j-, x, b,current_len,lcs_max_len);
}
else
{
Display_Lcs(i,j-,x,b,current_len,lcs_max_len);
Display_Lcs(i-,j,x,b,current_len,lcs_max_len);
}
} int main(int argc, char* argv[])
{
string x = "ABCBDAB";
string y = "BDCABA";
int xlen = x.length();
int ylen = y.length(); int b[X + ][Y + ]; int lcs_max_len = Lcs_Length( x, y, b, xlen,ylen );
cout << lcs_max_len << endl; Display_Lcs( xlen, ylen, x, b, lcs_max_len, lcs_max_len );
cout << "共有:" << cnt << "种"; return ;
}
运行结果如下:
BDAB
BCAB
BCBA
共有: 种
/****************************************
update
****************************************/
示例:
#include <iostream>
using namespace std;
#define X_LEN 7
#define Y_LEN 6
#define EQUAL 0
#define UP 1
#define LEVEL 2
void lcs_length(char* X,char* Y,int c[X_LEN+][Y_LEN+],int b[X_LEN+][Y_LEN+]);
void print_lcs(int b[X_LEN+][Y_LEN+],char *X,int i,int j); int main()
{
char X[X_LEN+] = {' ','A','B','C','B','D','A','B'};
char Y[Y_LEN+] = {' ','B','D','C','A','B','A'};
int c[X_LEN+][Y_LEN+]={};
int b[X_LEN+][Y_LEN+] = {};
int i,j;
lcs_length(X,Y,c,b);
for(i=;i<=X_LEN;i++)
{
for(j=;j<=Y_LEN;j++)
cout<<c[i][j]<<" ";
cout<<endl;
}
cout<<"The length of LCS is: "<<c[X_LEN][Y_LEN]<<endl;
cout<<"The longest common subsequence between X and y is: "<<endl;
print_lcs(b,X,X_LEN,Y_LEN);
return ;
}
//采用动态规划方法自底向上的进行计算,寻找最优解
void lcs_length(char* X,char* Y,int c[X_LEN+][Y_LEN+],int b[X_LEN+][Y_LEN+])
{
int i,j;
//设置边界条件,即i=0或者j=0
for(i=;i<X_LEN;i++)
c[i][] = ;
for(j=;j<Y_LEN;j++)
c[][j] = ;
for(i=;i<=X_LEN;i++)
for(j=;j<=Y_LEN;j++)
{
if(X[i] == Y[j]) //满足递归公式第二条
{
c[i][j] = c[i-][j-]+;
b[i][j] = EQUAL ;
}
else if(c[i-][j] >= c[i][j-]) //递归公式第三条
{
c[i][j] = c[i-][j];
b[i][j] = UP;
}
else
{
c[i][j] = c[i][j-];
b[i][j] = LEVEL;
}
}
}
void print_lcs(int b[X_LEN+][Y_LEN+],char *X,int i,int j)
{
if(i== || j==)
return;
if(b[i][j] == EQUAL)
{
print_lcs(b,X,i-,j-);
cout<<X[i]<<" ";
}
else
if(b[i][j] == UP)
print_lcs(b,X,i-,j);
else
print_lcs(b,X,i,j-);
}
结果:
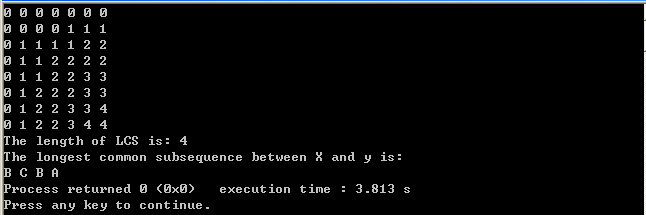
Algorithm --> 最长公共子序列(LCS)的更多相关文章
- 编程算法 - 最长公共子序列(LCS) 代码(C)
最长公共子序列(LCS) 代码(C) 本文地址: http://blog.csdn.net/caroline_wendy 题目: 给定两个字符串s,t, 求出这两个字符串最长的公共子序列的长度. 字符 ...
- POJ 1458 Common Subsequence(最长公共子序列LCS)
POJ1458 Common Subsequence(最长公共子序列LCS) http://poj.org/problem?id=1458 题意: 给你两个字符串, 要你求出两个字符串的最长公共子序列 ...
- 51nod 1006:最长公共子序列Lcs
1006 最长公共子序列Lcs 基准时间限制:1 秒 空间限制:131072 KB 分值: 0 难度:基础题 收藏 关注 给出两个字符串A B,求A与B的最长公共子序列(子序列不要求是连续的). ...
- 1006 最长公共子序列Lcs
1006 最长公共子序列Lcs 基准时间限制:1 秒 空间限制:131072 KB 给出两个字符串A B,求A与B的最长公共子序列(子序列不要求是连续的). 比如两个串为: abcicba abdks ...
- 动态规划之最长公共子序列LCS(Longest Common Subsequence)
一.问题描述 由于最长公共子序列LCS是一个比较经典的问题,主要是采用动态规划(DP)算法去实现,理论方面的讲述也非常详尽,本文重点是程序的实现部分,所以理论方面的解释主要看这篇博客:http://b ...
- C++版 - Lintcode 77-Longest Common Subsequence最长公共子序列(LCS) - 题解
版权声明:本文为博主Bravo Yeung(知乎UserName同名)的原创文章,欲转载请先私信获博主允许,转载时请附上网址 http://blog.csdn.net/lzuacm. C++版 - L ...
- 51Nod 1006:最长公共子序列Lcs(打印LCS)
1006 最长公共子序列Lcs 基准时间限制:1 秒 空间限制:131072 KB 分值: 0 难度:基础题 收藏 关注 给出两个字符串A B,求A与B的最长公共子序列(子序列不要求是连续的). ...
- 51nod 1006 最长公共子序列Lcs 【LCS/打印path】
1006 最长公共子序列Lcs 基准时间限制:1 秒 空间限制:131072 KB 分值: 0 难度:基础题 收藏 关注 给出两个字符串A B,求A与B的最长公共子序列(子序列不要求是连续的). ...
- 每日一题-——最长公共子序列(LCS)与最长公共子串
最长公共子序列(LCS) 思路: 代码: def LCS(string1,string2): len1 = len(string1) len2 = len(string2) res = [[0 for ...
随机推荐
- Davinci DM6446开发攻略——DSP开发工程建立
前段时间一直忙一个项目,同时在生活上时时提防和抵抗中国地沟油.国外核心转基因调和油.大豆油.色拉油.大米玉米.可怕的喂药鱼.药水泡农药喷无虫咬的青菜,所以没时间打理自己的博客,让开发攻略停顿了一段时间 ...
- Java中的Calendar方法
/** * @Title:JavaDate.java * @Package:com.yhd.chart.model * @Description:Java中的Calendar总结 * @author: ...
- PowerManager和PowerManager.WakeLock详解
最近在做项目过程中,有一个LocalPush的需求,需要保持屏幕点亮一段时间,并且在这个时间里,启动Service来执行请求服务器的操作,拿到热点的数据.所以,就找了一下相关的android开源项目. ...
- Excel 2010去掉网格线
怎么去掉Excel中的网格线? 具体错误步骤如下: 1.新建excel文件,双击打开文件 2.打开视图 3.取消勾选"网格线"
- Linux以字节显示内存大小
Linux以字节显示内存大小 youhaidong@youhaidong-ThinkPad-Edge-E545:~$ free -b total used free shared buffers ca ...
- dojo中表格行隐藏出错
1.错误描述 TypeError:role._by_idx[e.rowIndex].hide is not a function (54 out of range 3) 2.错误原 ...
- Java中的三目运算符
1.问题背景 以下代码运行的结果是: A.hai B.1987 C.1988 D.以上答案都不对 /** * 三目运算符 * A.hai * B.1987 * C.198 ...
- windows共享虚拟机ubuntu目录
1)安装 sudo apt-get install samba 2)配置文件vi /etc/samba/smb.conf 添加如下 3)启动服务 sudo service smbd start 4)w ...
- FFMPEG 在ubuntu下的安装与使用
转载自 http://www.cnblogs.com/dwdxdy/p/3240167.html (部分一:安装) ffmpeg的安装: 1.下载源文件(以ffmpeg1.2.1为例): http:/ ...
- linux之软件安装
一.软件包管理简介 1)软件包分类 1.源码包 优点: 开源, 如果有足够的能力, 可以修改源代码 可以自由选择所需的功能 软件是编译安装, 所以更加适合自己的系统, 更加稳定也效率更高 卸载方便 缺 ...
