[BJOI2006]狼抓兔子

题目描述

现在小朋友们最喜欢的"喜羊羊与灰太狼",话说灰太狼抓羊不到，但抓兔子还是比较在行的，而且现在的兔子还比较笨，它们只有两个窝，现在你做为狼王，面对下面这样一个网格的地形：

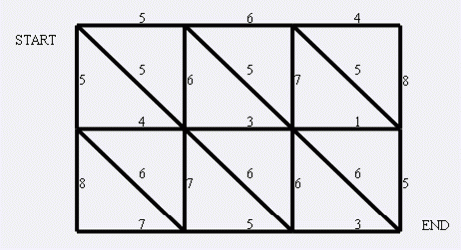
左上角点为(1,1),右下角点为(N,M)(上图中N=3,M=4).有以下三种类型的道路

1:(x,y)<==>(x+1,y)

2:(x,y)<==>(x,y+1)

3:(x,y)<==>(x+1,y+1)

道路上的权值表示这条路上最多能够通过的兔子数，道路是无向的. 左上角和右下角为兔子的两个窝，开始时所有的兔子都聚集在左上角(1,1)的窝里，现在它们要跑到右下角(N,M)的窝中去，狼王开始伏击这些兔子.当然为了保险起见，如果一条道路上最多通过的兔子数为K，狼王需要安排同样数量的K只狼，才能完全封锁这条道路，你需要帮助狼王安排一个伏击方案，使得在将兔子一网打尽的前提下，参与的狼的数量要最小。因为狼还要去找喜羊羊麻烦。

输入输出格式

输入格式：

第一行为N,M.表示网格的大小，N,M均小于等于1000.

接下来分三部分

第一部分共N行，每行M-1个数，表示横向道路的权值.

第二部分共N-1行，每行M个数，表示纵向道路的权值.

第三部分共N-1行，每行M-1个数，表示斜向道路的权值.

输出格式：

输出一个整数，表示参与伏击的狼的最小数量.

输入输出样例

输入样例#1：
复制

输出样例#1： 复制

14
把网格平面图转为对偶图
求最小割就转化为最短路

 #include<iostream>

 #include<cstdio>

 #include<cstring>

 #include<cmath>

 #include<algorithm>

 #include<queue>

 using namespace std;

 typedef long long lol;

 struct Node

 {

   int next,to;

   lol dis;

 }edge[];

 int head[],num;

 lol dist[],ans;

 int S,T,n,m,up[][],down[][],cnt;

 bool vis[];

 queue<int>Q;

 lol gi()

 {

   char ch=getchar();

   lol x=;

   while (ch<''||ch>'') ch=getchar();

   while (ch>=''&&ch<='')

     {

       x=x*+ch-'';

       ch=getchar();

     }

   return x;

 }

 void add(int u,int v,lol dis)

 {

   num++;

   edge[num].next=head[u];

   head[u]=num;

   edge[num].to=v;

   edge[num].dis=dis;

   num++;

   edge[num].next=head[v];

   head[v]=num;

   edge[num].to=u;

   edge[num].dis=dis;

 }

 void SPFA()

 {int i;

   memset(dist,/,sizeof(dist));

   Q.push(S);

   dist[S]=;

   while (Q.empty()==)

     {

       int u=Q.front();

       Q.pop();

       vis[u]=;

       for (i=head[u];i;i=edge[i].next)

     {

       int v=edge[i].to;

       if (dist[v]>dist[u]+edge[i].dis)

         {

           dist[v]=dist[u]+edge[i].dis;

           if (vis[v]==)

         {

           vis[v]=;

           Q.push(v);

         }

         }

     }

     }

 }

 int main()

 {int i,j,x;

   cin>>n>>m;

   if (n==&&m==)

     {

       cout<<;

       return ;

     }

   if (n==||m==)

     {

       if (m==) swap(n,m);

       ans=2e9;

       for (i=;i<m;i++)

     {

       x=gi();

       if (ans>x) ans=x;

     }

       cout<<ans;

       return ;

     }

   S=;

   for (i=;i<n;i++)

     {

       for (j=;j<m;j++)

     {

       up[i][j]=++cnt;

       down[i][j]=++cnt;

     }

     }

   T=++cnt;

   for (i=;i<=n;i++)

     {

       for (j=;j<m;j++)

     {

       x=gi();

       if (i==) add(S,up[][j],x);

       if (i==n) add(down[n-][j],T,x);

       if (i!=&&i!=n)

         add(down[i-][j],up[i][j],x);

     }

     }

   for (i=;i<n;i++)

     {

       for (j=;j<=m;j++)

     {

       x=gi();

       if (j==) add(down[i][],T,x);

       if (j==m) add(S,up[i][m-],x);

       if (j!=&&j!=m)

         add(down[i][j],up[i][j-],x);

     }

     }

   for (i=;i<n;i++)

     {

       for (j=;j<m;j++)

     {

       x=gi();

       add(up[i][j],down[i][j],x);

     }

     }

   SPFA();

   printf("%lld",dist[T]);

 }