Maximum Entropy Model(最大熵模型)初理解

0，熵的描述

熵（entropy）指的是体系的混沌的程度(可也理解为一个随机变量的不确定性)，它在控制论、概率论、数论、天体物理、生命科学等领域都有重要应用，在不同的学科中也有引申出的更为具体的定义，是各领域十分重要的参量。熵由鲁道夫·克劳修斯（Rudolf Clausius）提出，并应用在热力学中。后来在，克劳德·艾尔伍德·香农（Claude Elwood Shannon）第一次将熵的概念引入到信息论中来。----baidu

下面我们将从随机变量开始一步一步慢慢理解熵。

1，随机变量（random variable）

1.1 随机变量（random variable）

什么事随机变量？

表示随机现象（在一定条件下，并不总是出现相同结果的现象称为随机现象）各种结果的实值函数（一切可能的样本点）。如掷一颗骰子，它的所有可能结果是出现1点、2点、3点、4点、5点和6点 ，若定义X为掷一颗骰子时出现的点数，则X为一随机变量。

随机变量   X∈{1,2,3,4,5,6}

　　　　　　图(1)

1.2 随机变量概率(The probability of a random variable)

什么是随机变量的概率？

要全面了解一个随机变量，不但要知道它取哪些值，而且要知道它取这些值的规律，即要掌握它的概率分布。概率分布可以由分布函数刻画。若知道一个随机变量的分布函数，则它取任何值和它落入某个数值区间内的概率都可以求出。所以我们可以P(X=x)其中一种情况出现的概率。而P(X)我们叫它为概率分布函数。

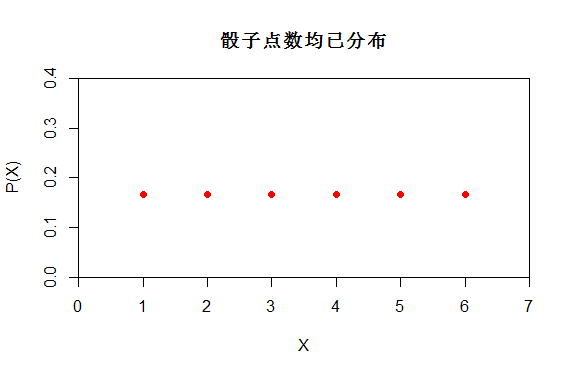
如上述掷一颗骰子，X是均匀分布 X~U[1,6]。而P(X)的分布函数如下，也可以看出P(X=1)=1/6

　　　　　　　　　　　　　　图(2)

又如某一地区的大学生身高为正态分布,若定义X为男性身高可能出现的值,则X也是一个随机变量，服从X~N(172.70, 8.01)。用P(X)表示随机变量的概率分布。

分布函数

　　　　　　　　　　　　　　　　　

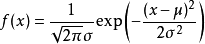
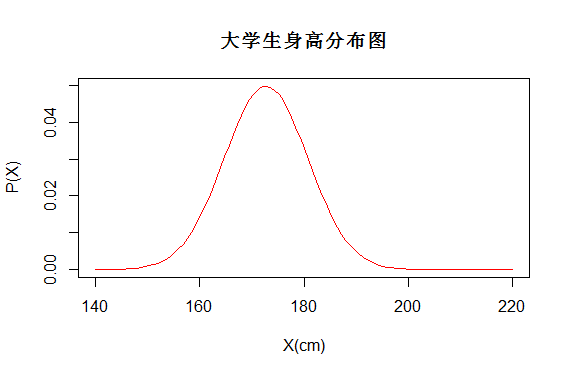
概率分布图如下，而每个学生的身高都对应了一个概率,如P(X=1.7)就能得到相应的概率

　　　　　　　　　　　　　　图(3)

1.3 随机变量的期望(Expected value)

期望又如何表示，表示什么？

假设随机变量X有值x1概率为p1,X有值x2概率为p2,..X有值xk概率为pk。则离散随机变量的期望可以定义为：

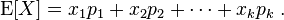
如骰子点数的期望E[X]=1/6(1+2+3+4+5+6)

其实期望就是我们生活中常常遇到的平均值，相当于用一个值简单的描述一个随机变量的分布情况与取值情况。

1.4 随机变量的随机性(randomness of a random variable)

如何刻画一个随机变量的随机性(不确定性)？

a:韦小宝用灌铅作弊骰子投掷的随机变量X更随机 还是我们用正常骰子投掷更随机呢？

明显正常骰子投掷更为随机。正常骰子投掷时有6种可能性{1,2,3,4,5,6}，而韦小宝投掷时只有一种可能性6.

b:那么随机性又是受什么影响呢？

X的值？明显不是！X取{1,2,3,4,5,6}与X取{2,3,4,5,6,7}可能性都是6种。

那么什么影响了X的随机性呢？

　　　　　　　　　　　　　　　　图(4)

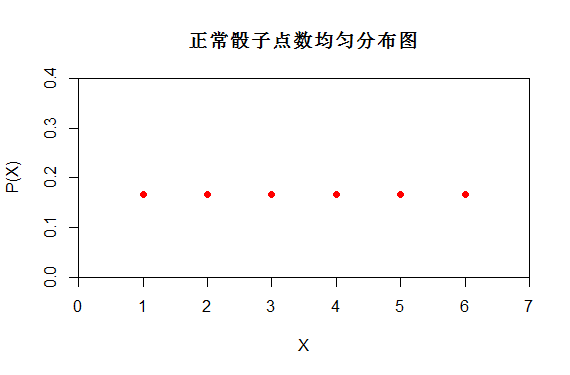
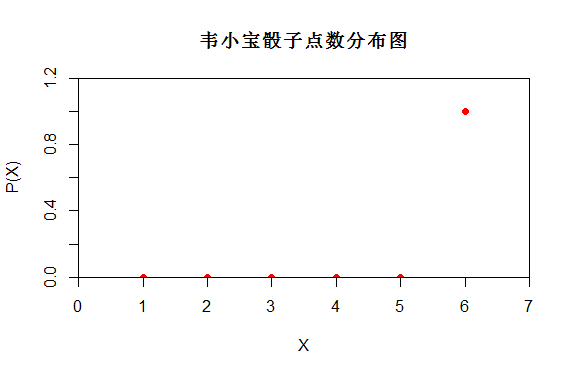
从上面对比图可以看出P(X)不同，它们的随机性不同。正常骰子的分布更为随机。

但是图(5)哪个随机变量分布哪个更随机呢？

第一个图服从均匀分布X~U(1,6)

第二个图服从高斯分布X~N(3.5,1)

两组都是X都是{1,2,3,4,5,6}只是它们取得概率不同。　

　　　　　　　　　　　　　　　　图(5)　　　　　　　　　　　　　　

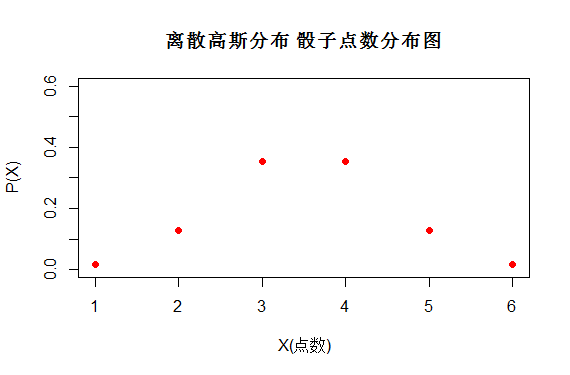
因此我们急需引入一个概念来表述随机变量的随机性，这也就是我们将要说的熵(Entropy)。

2, 最大熵原理(Principle of maximum entropy)

2.1 熵的定义

熵的计算公式：(为什么要将熵计算公式定义成这样？ 香农这样定义肯定有他的道理哈。在后面推导以及应用的时候就能感受到香农这么定义的强大。

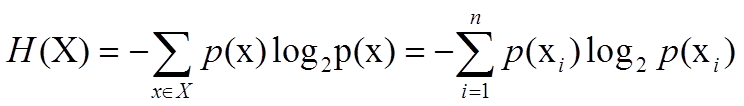
其中，x表示随机变量，与之相对应的是所有可能输出的集合，定义为符号集,随机变量的输出用x表示。P(x)表示输出概率函数。变量的不确定性越大，熵也就越大，把它搞清楚所需要的信息量也就越大.

现在我们可以用熵的公式来比较图4与5中到底哪个更随机了。

P(X)均匀分布，正常骰子投掷时的熵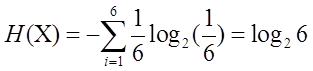：      =2.584963

P(X)特殊分布，韦小宝骰子投掷时的熵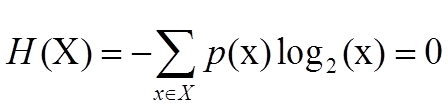：=0

P(X)正态分布，正态骰子投掷的熵：H(X)=2.028845

代入正态分布函数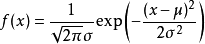，可以得到 6个点的概率分别为{ 0.0175283 0.1295176 0.3520653 0.3520653 0.1295176 0.0175283}

代入公式H(X)可以推出H(X)=

-(0.0175283*log2(0.0175283)+
   0.1295176*log2(0.1295176)+
   0.3520653*log2(0.3520653)+
   0.3520653*log2(0.3520653)+
   0.1295176*log2(0.1295176)+
   0.0175283*log2(0.0175283)
  )=2.028845

故得出结论:对于投掷骰子这个事件，随机变量X,当X概率分布P(X)是均匀分布时，熵H(X)值最大，是最随机的。

猜测：对于一个随机变量X,当它的分布是均匀分布时，它的熵H(X)是最大的(X是最随机的)。       这也就是我们说的最大熵。

2.2 单约束 最大熵推导

单约束最大熵的基本想法就是在一定条件下(概率和为1)，找到一个分布p*(X),使熵H(X)的值达到最大。可以写成：

　　　　　　　　

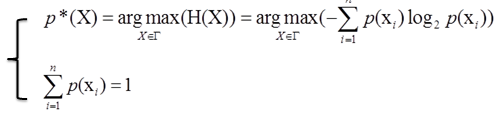
在约束下求最大值，使用拉格朗日乘子法。设

                

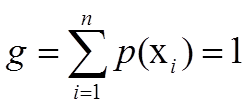
推出拉格朗日方程

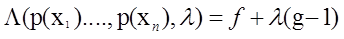
要求最大值，则考虑对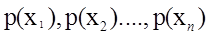求偏到导得到：

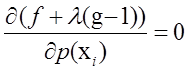      可以改写成：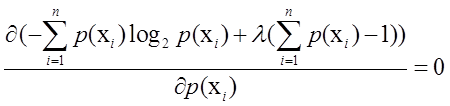

=>  

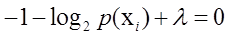
从而得到方程组

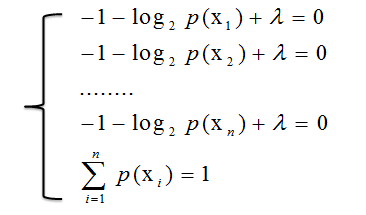           得到   

得到

证明猜想是正确的，一个随机变量X，当p(X)为均匀分布时，熵H(X)最大。

2.3 多约束 最大熵推导

多约束最大熵的基本想法就是在多个条件下(共m+1个约束)，找到一个分布p*(X),使熵H(X)的值达到最大。可以写成：

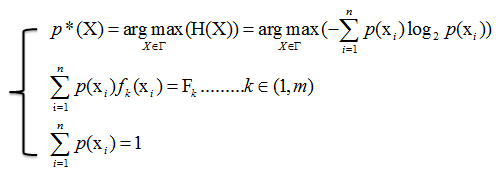
设

=>拉格朗日方程

对所有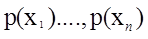求偏导

=>   

=>

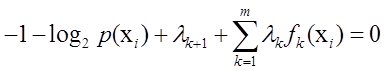
又因为：

=> 

=>

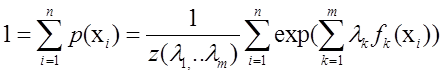
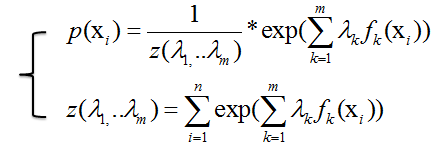
3，最大熵模型(Maximum Entropy Model)

上面讲的都是关于一个随机变量的熵H(X)，对于条件概率模型P(Y|X)的条件熵H(Y|X)也常常被用到，定义为

其中集合Z包含变量X,Y的所有范围。(x,y都是向量)

具体推导如下：

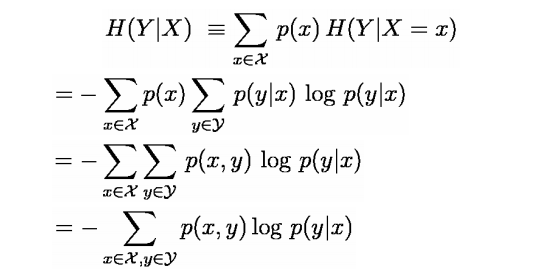
求最大熵就相当于求一个条件分布p(y|x)使得条件熵H(y|x)最大,其中x,y表示向量

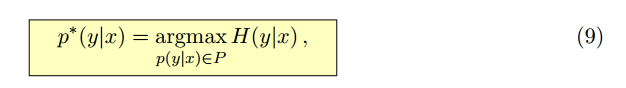
已知存在m+1个约束：

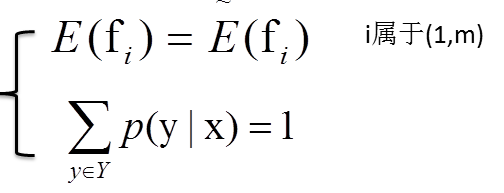
而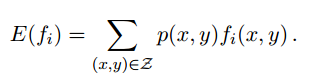

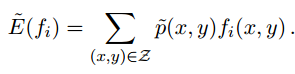
p(x,y)表示边缘概率，f(x,y)表示x与y的函数，~p(x,y)表示经验分布

使用拉格朗日乘子法可以得到拉格朗日方程：

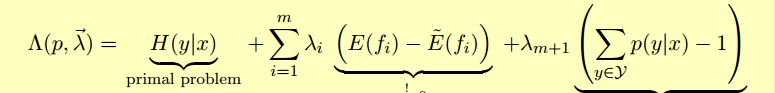
于各个部分对p(x1),p(x2)...求偏导数，

最后解方程可得

具体推导请看 http://pan.baidu.com/s/1i31hnEX

4，图模型表示

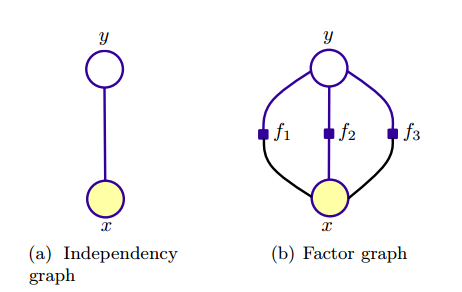
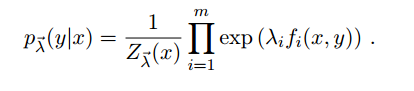
5，引用

http://pan.baidu.com/s/1i31hnEX

http://pan.baidu.com/s/1ntBO2pj

http://pan.baidu.com/s/1nt9M7ln

http://pan.baidu.com/s/1o6v7vfW

http://pan.baidu.com/s/1hqvJ9lE

http://pan.baidu.com/s/1qWHhYSO