用go实现常用算法与数据结构——队列(queue)

queue 简介

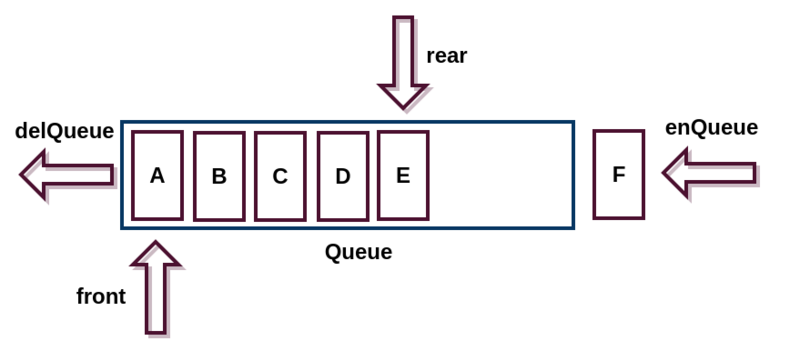
队列是一种非常常见的数据结构，日常生活中也能经常看到。一个典型的队列如下图(图片来自 segmentfault)：



可以看出队列和我们日常生活中排队是基本一致的。都遵循 FIFO(First In First Out)的原则。

实现

队列可以使用链表或者数组实现，使用链表的优点是扩容简单，缺点是无法通过索引定位元素，使用数组则相反，扩容不容易但是可以通过索引定位元素。文章采用双向链表实现。代码放在github：

https://github.com/AceDarkknight/AlgorithmAndDataStructure/tree/master/queue

链表一般有下面这几个基本操作，先定义一个接口，方便开发和测试：

type Queue interface {
    // 获取当前链表长度。
	Length() int
	// 获取当前链表容量。
	Capacity() int
	// 获取当前链表头结点。
	Front() *Node
	// 获取当前链表尾结点。
	Rear() *Node
	// 入列。
	Enqueue(value interface{}) bool
	// 出列。
	Dequeue() interface{}
}

笔者的实现中，front 和 rear 节点不保存具体值，只是用来指示真正头尾节点的位置。

链表实现的队列

入列的实现如下：

// normalQueue.go
func (q *NormalQueue) Enqueue(value interface{}) bool {
	if q.length == q.capacity || value == nil {
		return false
	}

	node := &Node{
		value: value,
	}

	if q.length == 0 {
		q.front.next = node
	}

	node.previous = q.rear.previous
	node.next = q.rear
	q.rear.previous.next = node
	q.rear.previous = node
	q.length++

	return true
}

出列的实现：

// normalQueue.go
func (q *NormalQueue) Dequeue() interface{} {
	if q.length == 0 {
		return nil
	}

	result := q.front.next
	q.front.next = result.next
	result.next = nil
	result.previous = nil
	q.length--

	return result.value
}

可以看到，具体实现和链表基本一致，这种方法好处在于不需要考虑数组溢出的问题。但是有时候，我们可能会向 queue 插入相同的元素，我们当前的实现是无法判断数据是否已经存在的，这时我们就需要实现一个无重复元素的 queue。

无重复元素的队列。

我们只需要在原来的基础上加一个 Map 存放我们的具体值就可以了。直接上代码：

// uniqueQueue.go
func (q *UniqueQueue) Enqueue(value interface{}) bool {
	if q.length == q.capacity || value == nil {
		return false
	}

	node := &Node{
		value: value,
	}

	// Ignore uncomparable type.
	if kind := reflect.TypeOf(value).Kind(); kind == reflect.Map || kind == reflect.Slice || kind == reflect.Func {
		return false
	}

	if v, ok := q.nodeMap[value]; ok || v {
		return false
	}

	if q.length == 0 {
		q.front.next = node
	}

	node.previous = q.rear.previous
	node.next = q.rear
	q.rear.previous.next = node
	q.rear.previous = node

	q.nodeMap[value] = true

	q.length++

	return true
}

因为在 golang 中，map 的 key 必须是可以比较的，所以我们需要排除 Map、slice、function 这些不可比较的类型。剩下的实现和上面的就差不多了。再看出列操作：

// uniqueQueue.go
func (q *UniqueQueue) Dequeue() interface{} {
	if q.length == 0 {
		return nil
	}

	result := q.front.next

	delete(q.nodeMap, result.value)

	q.front.next = result.next
	result.next = nil
	result.previous = nil

	q.length--

	return result.value
}

上面两个队列都是基于链表实现的，下面介绍一下基于数组实现的循环队列。

循环队列

循环队列通过复用数组元素来达到“循环”的效果。简单来说就是如果数组前面有位置，就把元素放进去。具体原理可以看这里。入列代码如下：

// cyclicQueue.go
func (q *CyclicQueue) Enqueue(value interface{}) bool {
	if q.length == q.capacity || value == nil {
		return false
	}

	node := &Node{
		value: value,
	}

	index := (q.rear + 1) % cap(q.nodes)
	q.nodes[index] = node
	q.rear = index
	q.length++

	if q.length == 1 {
		q.front = index
	}

	return true
}

出列操作也类似：

// cyclicQueue.go
func (q *CyclicQueue) Dequeue() interface{} {
	if q.length == 0 {
		return nil
	}

	result := q.nodes[q.front].value
	q.nodes[q.front] = nil
	index := (q.front + 1) % cap(q.nodes)
	q.front = index
	q.length--

	return result
}

Reference

https://www.geeksforgeeks.org/queue-set-1introduction-and-array-implementation/