Vladik and cards

Vladik and cards

time limit per test

2 seconds

memory limit per test

256 megabytes

input

standard input

output

standard output

Vladik was bored on his way home and decided to play the following game. He took n cards and put them in a row in front of himself. Every card has a positive integer number not exceeding 8 written on it. He decided to find the longest subsequence of cards which satisfies the following conditions:

• the number of occurrences of each number from 1 to 8 in the subsequence doesn't differ by more then 1 from the number of occurrences of any other number. Formally, if there are ck cards with number k on them in the subsequence, than for all pairs of integers 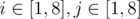 the condition |ci - cj| ≤ 1 must hold.
• if there is at least one card with number x on it in the subsequence, then all cards with number x in this subsequence must form a continuous segment in it (but not necessarily a continuous segment in the original sequence). For example, the subsequence[1, 1, 2, 2] satisfies this condition while the subsequence [1, 2, 2, 1] doesn't. Note that [1, 1, 2, 2] doesn't satisfy the first condition.

Please help Vladik to find the length of the longest subsequence that satisfies both conditions.

Input

The first line contains single integer n (1 ≤ n ≤ 1000) — the number of cards in Vladik's sequence.

The second line contains the sequence of n positive integers not exceeding 8 — the description of Vladik's sequence.

Output

Print single integer — the length of the longest subsequence of Vladik's sequence that satisfies both conditions.

Examples

input

3
1 1 1

output

1

input

8
8 7 6 5 4 3 2 1

output

8

input

24
1 8 1 2 8 2 3 8 3 4 8 4 5 8 5 6 8 6 7 8 7 8 8 8

output

17

Note

In the first sample all the numbers written on the cards are equal, so you can't take more than one card, otherwise you'll violate the first condition.

分析：状压dp；

　　　dp[i][j]表示到i为止j里面二进制1表示这个位置的数是否用过的取len+1的个数的最大值；

代码：

#include <iostream>
#include <cstdio>
#include <cstdlib>
#include <cmath>
#include <algorithm>
#include <climits>
#include <cstring>
#include <string>
#include <set>
#include <map>
#include <queue>
#include <stack>
#include <vector>
#include <list>
#define rep(i,m,n) for(i=m;i<=n;i++)
#define rsp(it,s) for(set<int>::iterator it=s.begin();it!=s.end();it++)
#define mod 1000000007
#define inf 0x3f3f3f3f
#define vi vector<int>
#define pb push_back
#define mp make_pair
#define fi first
#define se second
#define ll long long
#define pi acos(-1.0)
#define pii pair<int,int>
#define Lson L, mid, ls[rt]
#define Rson mid+1, R, rs[rt]
#define sys system("pause")
#define intxt freopen("in.txt","r",stdin)
const int maxn=1e3+;
using namespace std;
ll gcd(ll p,ll q){return q==?p:gcd(q,p%q);}
ll qpow(ll p,ll q){ll f=;while(q){if(q&)f=f*p;p=p*p;q>>=;}return f;}
inline void umax(int&p,int q){if(p<q)p=q;}
inline ll read()
{
    ll x=;int f=;char ch=getchar();
    while(ch<''||ch>''){if(ch=='-')f=-;ch=getchar();}
    while(ch>=''&&ch<=''){x=x*+ch-'';ch=getchar();}
    return x*f;
}
int n,m,k,t,pos[][maxn],dp[maxn][<<],cur[],a[maxn],ans;
bool ok(int len)
{
    memset(dp,-inf,sizeof(dp));
    memset(cur,,sizeof(cur));
    dp[][]=;
    bool flag=false;
    for(int i=;i<=n;i++)
    {
        for(int j=;j<(<<);j++)
        {
            if(dp[i][j]==-inf)continue;
            for(int k=;k<=;k++)
            {
                if(j&(<<(k-)))continue;
                if(cur[k]+len>pos[k][])continue;
                int now_pos=pos[k][cur[k]+len];
                umax(dp[now_pos][j|(<<(k-))],dp[i][j]);
                if(cur[k]+len+>pos[k][])continue;
                now_pos=pos[k][cur[k]+len+];
                umax(dp[now_pos][j|(<<(k-))],dp[i][j]+);
            }
        }
        cur[a[i]]++;
    }
    for(int i=;i<=n+;i++)
    {
        if(dp[i][(<<)-]>=)
        {
            flag=true;
            ans=max(ans,dp[i][(<<)-]*(len+)+(-dp[i][(<<)-])*len);
        }
    }
    return flag;
}
int main()
{
    int i,j;
    scanf("%d",&n);
    rep(i,,n)a[i]=read();
    rep(i,,n)
    {
        pos[a[i]][++pos[a[i]][]]=i;
    }
    rep(i,,)if(pos[i][])ans++;
    int l=,r=n/;
    while(l<=r)
    {
        int mid=l+r>>;
        if(ok(mid))l=mid+;
        else r=mid-;
    }
    printf("%d\n",ans);
    //system("Pause");
    return ;
}