c++中的全排列

next_permutation函数

组合数学中经常用到排列，这里介绍一个计算序列全排列的函数：next_permutation（start,end），和prev_permutation（start,end）。这两个函数作用是一样的，区别就在于前者求的是当前排列的下一个排列，后一个求的是当前排列的上一个排列。至于这里的“前一个”和“后一个”，我们可以把它理解为序列的字典序的前后，严格来讲，就是对于当前序列pn，他的下一个序列pn+1满足：不存在另外的序列pm，使pn<pm<pn+1.

对于next_permutation函数，其函数原型为：

#include <algorithm>

bool next_permutation(iterator start,iterator end)

当当前序列不存在下一个排列时，函数返回false，否则返回true

同时，相对应的，上一个排列即为prev_permutation(int *begin, int *end)

看如下代码：

#include <iostream>
#include <algorithm>
using namespace std;
int main()
{
    int num[]={,,};
    do
    {
        cout<<num[]<<" "<<num[]<<" "<<num[]<<endl;
    }while(next_permutation(num,num+));
    return ;
}  

运行结果如图：

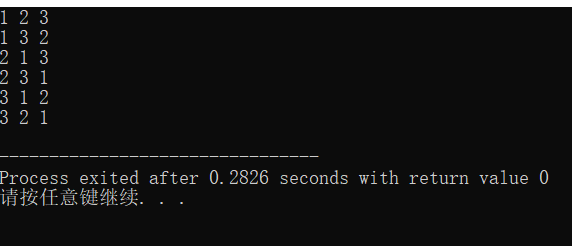
注意：当我们把while(next_permutation(num,num+3))中的3改为2时，输出就变为了下图所示：

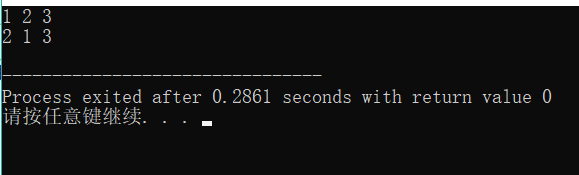
说明此时只针对1，2进行了全排列，有两个，后面的3没有变化，同时改变了数组前两个的值。

由此可以看出，next_permutation(num,num+n)函数是对数组num中的前n个元素进行全排列，同时并改变num数组的值。

另外，需要强调的是，next_permutation（）在使用前需要对欲排列数组按升序排序，否则只能找出该序列之后的全排列数。

比如，如果数组num初始化为3,1,2，那么输出就变为了：

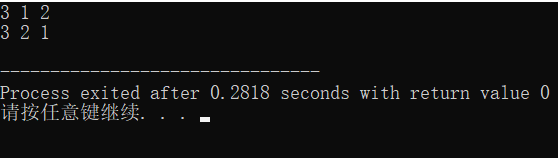
维基百科上全排列的实现：

循环法：

#include <iostream>
using namespace std;
bool arrsame(int* arr, int len, int num) {
    int i;
    for (i = ; i < len; i++)
        if (arr[i] == num)
            break;
    return i != len;
}
bool next_perm(int* perm, const int k, const int n) {
    int i = k - ;
    do
        perm[i]++;
    while (arrsame(perm, i, perm[i]) || (perm[i] >= n && i--));
    if (perm[] >= n)
        return ;
    for (int num = , seat = i + ; seat < k; num++)
        if (!arrsame(perm, i + , num))
            perm[seat++] = num;
    return ;
}
int main() {
    int n, k;
    cout << "perm(n,k):" << endl;
    cin >> n >> k;
    if (n < k || k <= )
        return ;
    int* perm = new int[k];
    for (int i = ; i < k; i++)
        perm[i] = i;
    do
        for (int i = ; i < k; cout << ((++i < k) ? ',' : '\n'))
            cout << perm[i] + ;
    while (next_perm(perm, k, n));
    delete[] perm;
    return ;
}

递归法：

#include <bits/stdc++.h>
using namespace std;

struct prem {
    int len;
    vector<int> used, position;
    function<void(vector<int>&)> action;
    prem(int l = , function<void(vector<int>&)> a = [](vector<int>& position) {}) : len(l), used(l, -), position(l), action(a) {}
    void run(int now = -) {
        if (now == len - ) {
            action(position);
            return;
        }
        int next = now + ;
        for (int i = ; i < len; i++) {
            if (used[i] == -) {
                used[i] = next;
                position[next] = i;
                run(next);
                used[i] = -;
            }
        }
    }
};
int main() {
    ios::sync_with_stdio(false), cin.tie();
    int len = ;
    prem p(len, [&](vector<int>& p) {
        for (int i = ; i < len; i++) {
            cout << p[i] << " ";
        }
        cout << endl;
    });
    p.run();
    return ;
}

next_permutation 可以自定义比较函数 例如：POJ 1256

题目中要求的字典序是：A'<'a'<'B'<'b'<...<'Z'<'z'，所以在用函数之前必须得按照题目要求的进行排序

#include<iostream> //poj 1256 Anagram
#include<string.h>
#include<algorithm>
using namespace std;
int cmp(char a,char b)
{
 if(tolower(a)!=tolower(b))//tolower 是将大写字母转化为小写字母.
 return tolower(a)<tolower(b);
 else
 return a<b;
}
int main()
{
 char ch[];
 int n;
cin>>n;
 while(n--)
{
scanf("%s",ch);
sort(ch,ch+strlen(ch),cmp);
 do
{
printf("%s\n",ch);
}while(next_permutation(ch,ch+strlen(ch),cmp));
}
 return ;
}

.