【作业1.0】OO第一单元作业总结

OO第一单元作业已全部完成，为了使这一单元的作业能够收获更多一点，我回忆起我曾经在计算机组成课设中，经常我们会写一些实验报告，经常以此对实验内容反思总结。在我们开始下一单元的作业之前，我在此对OO第一单元进行总体性的反思总结，请各位助教和同学们批评指正！

一、程序结构分析

1. 代码规模度量

第一次作业

类	类总代码规模	类属性个数	类方法个数
"MainClass"	8	0	1
"Polynomial"	150	10	4
"Term"	36	2	5

方法	控制分支数目	方法规模
"MainClass.main(String[])"	0	6
"Polynomial.Polynomial(String)"	1	10
"Polynomial.diff()"	3	13
"Polynomial.initialize(Matcher)"	6	29
"Polynomial.printDiff()"	12	56
"Polynomial.standardize()"	6	29
"Term.Term(BigInteger,BigInteger)"	0	4
"Term.compareTo(Term)"	4	16
"Term.getCoe()"	0	3
"Term.getPow()"	0	3
"Term.setCoe(BigInteger)"	0	3
"Term.setPow(BigInteger)"	0	3

第二次作业

类	类总代码规模	类属性个数	类方法个数
"Expression"	157	11	9
"MainClass"	20	0	1
"Term"	206	7	21

方法	控制分支数目	方法规模
"Expression.Expression()"	0	5
"Expression.Expression(String)"	0	5
"Expression.addTerm(Term)"	0	3
"Expression.diff()"	1	6
"Expression.getDeriFunc()"	0	3
"Expression.getPrimFunc()"	0	3
"Expression.parse()"	1	10
"Expression.printDiff()"	7	35
"Expression.standardize()"	12	60
"Expression.trim(String)"	0	5
"Expression.validCheck()"	0	9
"MainClass.main(String[])"	2	18
"Term.Term()"	0	3
"Term.Term(String)"	8	29
"Term.addFactors(Expression)"	0	3
"Term.compareTo(Term)"	8	28
"Term.diff()"	6	37
"Term.getCoe()"	0	3
"Term.getCosPow()"	0	3
"Term.getEksPow()"	0	3
"Term.getFactors()"	0	3
"Term.getSinPow()"	0	3
"Term.isCosine(String)"	0	5
"Term.isDigit(String)"	0	5
"Term.isEks(String)"	0	5
"Term.isSine(String)"	0	5
"Term.setCoe(BigInteger)"	0	3
"Term.setCosPow(BigInteger)"	0	3
"Term.setEksPow(BigInteger)"	0	3
"Term.setSinPow(BigInteger)"	0	3
"Term.similarTo(Term)"	3	12
"Term.toCosine(String)"	1	9
"Term.toDigit(String)"	1	10
"Term.toEks(String)"	1	9
"Term.toSine(String)"	1	9

第三次作业

类	类总代码规模	类属性个数	类方法个数
"MainClass"	45	0	2
"factor.Coefficient"	45	1	7
"factor.Cosine"	73	6	6
"factor.Eks"	54	4	7
"factor.FactorFactory"	56	9	5
"factor.Sine"	73	6	6
"factor.SubExp"	53	1	7
"main.Expression"	182	12	8
"main.Term"	123	12	9

方法	控制分支数目	方法规模
"MainClass.bracketLayer(String)"	6	28
"MainClass.main(String[])"	1	15
"factor.Coefficient.Coefficient(String)"	0	3
"factor.Coefficient.equals(Factor)"	1	7
"factor.Coefficient.getDiff()"	0	6
"factor.Coefficient.getPow()"	0	4
"factor.Coefficient.getSubFac()"	0	4
"factor.Coefficient.getType()"	0	4
"factor.Coefficient.print()"	0	4
"factor.Coefficient.toDigit(String)"	1	10
"factor.Cosine.Cosine(BigInteger,Factor)"	0	4
"factor.Cosine.Cosine(String)"	3	16
"factor.Cosine.equals(Factor)"	2	10
"factor.Cosine.getDiff()"	1	16
"factor.Cosine.getPow()"	0	4
"factor.Cosine.getSubFac()"	0	4
"factor.Cosine.getType()"	0	4
"factor.Cosine.print()"	1	7
"factor.Eks.Eks(String)"	1	6
"factor.Eks.equals(Factor)"	1	7
"factor.Eks.getDiff()"	0	7
"factor.Eks.getPow()"	0	4
"factor.Eks.getSubFac()"	0	4
"factor.Eks.getType()"	0	4
"factor.Eks.print()"	1	7
"factor.Eks.toEks(String)"	1	9
"factor.FactorFactory.getFactor(String)"	6	25
"factor.FactorFactory.isCosine(String)"	0	5
"factor.FactorFactory.isDigit(String)"	0	5
"factor.FactorFactory.isEks(String)"	0	5
"factor.FactorFactory.isSine(String)"	0	5
"factor.Sine.Sine(BigInteger,Factor)"	0	4
"factor.Sine.Sine(String)"	3	16
"factor.Sine.equals(Factor)"	2	10
"factor.Sine.getDiff()"	1	16
"factor.Sine.getPow()"	0	4
"factor.Sine.getSubFac()"	0	4
"factor.Sine.getType()"	0	4
"factor.Sine.print()"	1	7
"factor.SubExp.SubExp(ArrayList)"	1	6
"factor.SubExp.SubExp(String)"	0	11
"factor.SubExp.equals(Factor)"	1	7
"factor.SubExp.getDiff()"	0	7
"factor.SubExp.getPow()"	0	4
"factor.SubExp.getSubExp()"	0	3
"factor.SubExp.getSubFac()"	0	4
"factor.SubExp.getType()"	0	4
"factor.SubExp.print()"	0	4
"main.Expression.Expression()"	0	5
"main.Expression.Expression(String)"	0	5
"main.Expression.addTerm(Term)"	0	3
"main.Expression.diff()"	1	6
"main.Expression.getDeriFunc()"	0	3
"main.Expression.getPrimFunc()"	0	3
"main.Expression.parse()"	7	30
"main.Expression.print(int)"	8	52
"main.Expression.standardize()"	0	50
"main.Expression.validCheck()"	1	11
"main.Term.Term()"	0	5
"main.Term.Term(String)"	9	29
"main.Term.addFactors(Factor)"	0	3
"main.Term.compareTo(Term)"	4	16
"main.Term.diff()"	6	30
"main.Term.getCoe()"	0	3
"main.Term.getEksPow()"	0	3
"main.Term.getFactors()"	0	3
"main.Term.setCoe(BigInteger)"	0	3
"main.Term.setEksPow(BigInteger)"	0	3
"main.Term.similarTo(Term)"	2	10

从三次作业的数据可以看出，类的个数不断增加，代码总规模显著增加；类的方法个数、属性个数变化较少。这符合作业题目中，功能不断迭代增加，而处理的基本流程不变的特点。

方法的平均行数也不断减小，代码的可读性有所增加。

2. 代码复杂度、耦合性度量

笔者使用了IDEA内置的MetricsReloaded插件进行度量，其中主要包括以下几个参数（摘自学长博客）：

ev(G)基本复杂度，是用来衡量程序非结构化程度的，非结构成分降低了程序的质量，增加了代码的维护难度，使程序难于理解。因此，基本复杂度高意味着非结构化程度高，难以模块化和维护。实际上，消除了一个错误有时会引起其他的错误。

Iv(G)模块设计复杂度，是用来衡量模块判定结构，即模块和其他模块的调用关系。软件模块设计复杂度高意味模块耦合度高，这将导致模块难于隔离、维护和复用。模块设计复杂度是从模块流程图中移去那些不包含调用子模块的判定和循环结构后得出的圈复杂度，因此模块设计复杂度不能大于圈复杂度，通常是远小于圈复杂度。

v(G)圈复杂度，是用来衡量一个模块判定结构的复杂程度，数量上表现为独立路径的条数，即合理的预防错误所需测试的最少路径条数，圈复杂度大说明程序代码可能质量低且难于测试和维护，经验表明，程序的可能错误和高的圈复杂度有着很大关系。

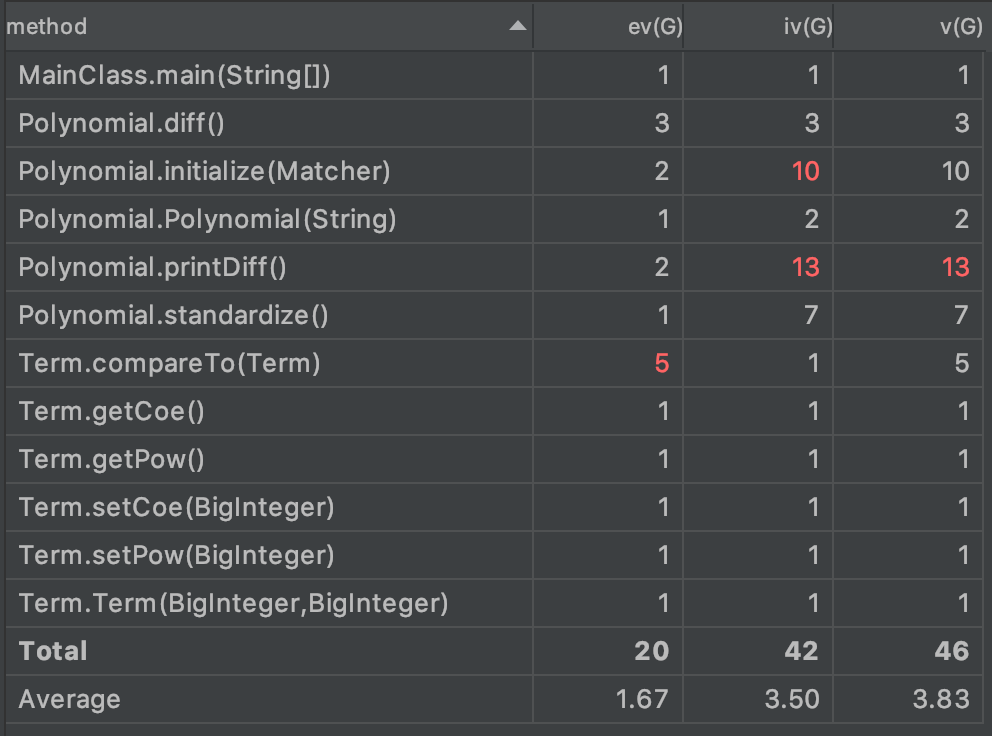
第一次作业

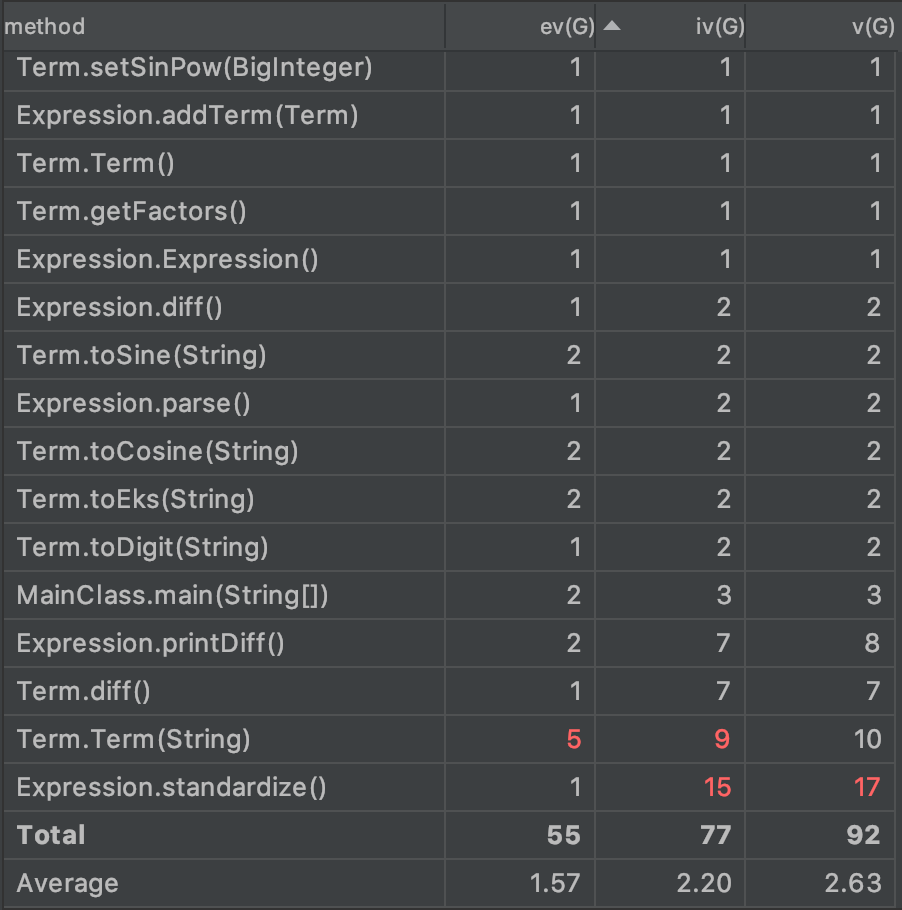
第二次作业

第三次作业

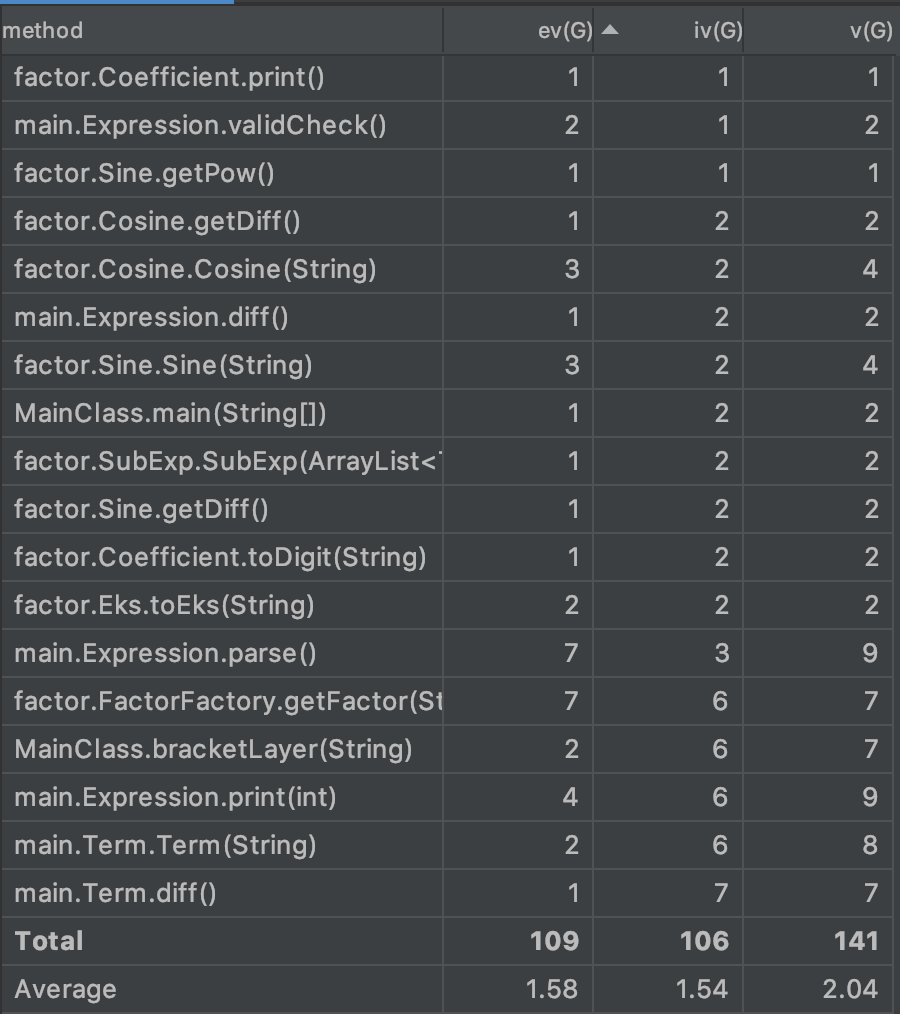
从图中可以看出，三次作业的平均复杂度呈下降趋势，也恰好证明了笔者在对三次作业进行迭代时，对代码结构不断重构并解耦的过程。

可以看到，超标的方法是Polynomial.initialize()和Polynomial.printDiff()。前者因为负责了全部的字符串解析工作而较为臃肿，后者涉及了复杂的格式处理，因而不够简洁。

在此需要特别注意的是输出（print）方法，简化表达式（standardize）方法以及Term的构造方法均出现了复杂度超标的现象。

输出复杂度超标的原因，主要是在输出时对系数和指数是0，±1等特殊情况做了较为复杂的判断；尤其是前两次作业，笔者没能够将复杂的输出逻辑简化到项（Term）的层面进行，因此使得表达式的输出模块较为臃肿。

简化表达式涉及到对方法参数（为一个引用）所指向实体的修改，因此使得耦合度大幅上升。笔者在开始构造这一模块时并没有想到这样做会带来危险；经过学习后发现，最好的处理方法还是将得到的优化后的表达式作为返回值返回，而不是直接对引用实体进行修改，这样可以避免后期作业中，递归表达式对外层表达式做不期望的修改。

这一单元的第二次作业中，自作聪明的我在Term等子类的创建逻辑全部放在了构造方法里面，这样就可以直接通过一个new Term(input)操作直接得到表达式需要的项（也正因如此，我没能够认识到工厂方法的优势）。但在阅读了学长的博客之后，我发现了这样做的问题：在《阿里巴巴Java开发手册》中有这样的描述：【强制】构造方法里面禁止加入任何业务逻辑,如果有初始化逻辑,请放在init方法中。进一步查阅资料后，我才明白，这样做会给后续的依赖、扩展造成困难，第三次作业的开发也证实了这一点，我不得不通过方法重载来实现递归表达式的Term创建。

第三次作业我便改用了FactorFactory函数，用工厂方法模式创建需要的因子。此时Term的构造方法耦合度明显下降（但FactorFactory工厂方法略微臃肿）。

3. 扩展DIT

前两次作业内容较少，笔者没有采用抽象类继承或接口实现的方法。第三次作业中，由于使用了FactorFactory的工厂方法模式，因此使用了Factor接口，共有Coefficient（常数因子）、Eks（基本变量x）、Sine（sin函数）、Cosine（cos函数）、SubExp（子表达式）五中因子类实现了Factor接口。接口的实现深度为1。

4. 类图

第一次作业

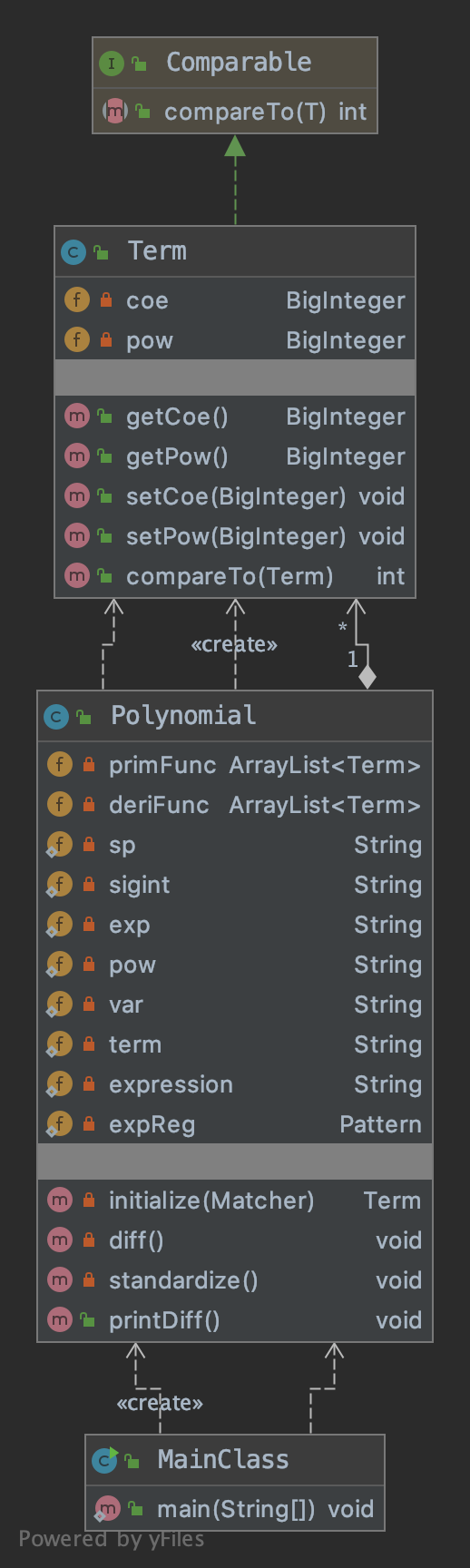
第一次作业中，我使用了三个类。MainClass只负责输入输出，Polynomial负责对多项式进行解析和求导，Term类的示例为多项式中的项对象。

我认为这次作业中成功之处在于：

1. 主类MainClass的保持了清晰的结构和简短的代码，将一切解析和计算交给其他类。
2. 使用了ArrayList容器储存项，便于多项式的元素增删以及排序。
3. 对表达式进行了充分的化简。

失败之处在于：

1. 所有的解析、计算工作均交给了Polynomial类，使得其内容过于臃肿，很多方法濒临超行数限制。而且方法的使用有显著的面向过程意味。
2. 没有充分发挥Term类的作用，几乎只将其作为一个静态结构体使用。
3. 可扩展性不强，没有很好地符合开闭原则。

第二次作业

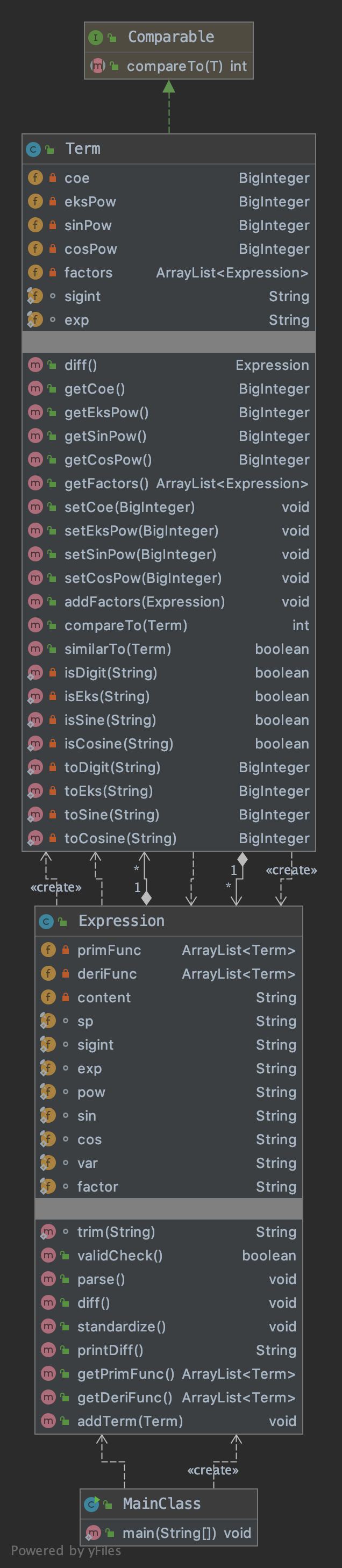
第二次作业大体继承了第一次作业的架构，主要为Term方法添加了SinPow和CosPow两个属性，并为之添加了相应的计算逻辑和化简逻辑。

我认为这次作业的成功之处在于：

1. 对第一次作业的架构进行了很好的复用。
2. 将sin、cos的系数作为Term的属性，便于计算和化简。

失败之处在于：

1. 经过添加三角函数的业务逻辑之后，Term类开始变得臃肿，维护困难
2. 没有对未来的需求做很好的预估，留出的迭代空间没能为第三次作业服务
3. 在第一次作业的模块中添加代码的行为不符合开闭原则。

第三次作业

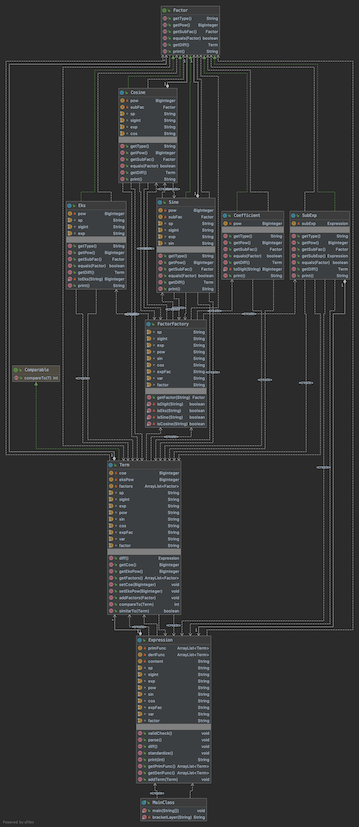
第三次作业进行了较大的结构变动，但具体的实现过程和第二次类似。为了求稳，很多优化优化过程也被去除。

这次作业的成功之处在于：

1. 使用接口Factor统一了各种因子的用法，简化了上一级类Term的负担。
2. 使用工厂方法完成对各种因子的创建，便于扩展。（虽然已经没有继续扩展的作业了）
3. 在题目存在递归表达式的情况下，仍然使用正则表达式完成了很高效的处理：
   第三次作业中，我在括号后使用“{@@…@}”对括号进行嵌套层级的标注，正则表达式匹配时，自动忽略内层字符，只对外层进行正确性判断和解析，内层交给递归生成的类处理。

失败之处在于：

1. 细节处理不到位：这次作业首次出现了bug，分别因输出优化、格式判断造成。两处bug实质上均属于格式处理的问题，是同质bug
2. 优化不到位：第三次作业的优化性能和第二次相比有所退步，因为正余弦函数在这次作业中变成了一个对象（可能含有递归嵌套），而不再只是属性，若使用.equals()嵌套比较同类项，会出现很长的回溯，很容易超时。这一问题的解决可能需要放弃正则表达式，寻求更加底层的处理方式（比如状态机）。

二、分析自己程序的bug

第一次作业

第一次作业中，公测和互测均未出现bug，笔者自己也没有检查出bug。

第二次作业

第二次作业中，公测和互测均未出现bug，但笔者自己在互测阶段再次发现bug，是在三角函数输出结果的次幂为-1时的格式错误。例如：当生成的表达式为sin(x)**-1*cos(x)时，程序将-1误判为cos(x)的系数进行化简，得到了sin(x)**-cos(x)的结果。

第三次作业

第三次作业中，公测和互测均出现bug，和第二次作业类似，分别是输入和输出时发生的格式错误。在内层表达式解析时，笔者通过去掉输入字符串的前三个和后三个字符（“({}”和“){}”）来得到内层嵌套，但忽略了前后空格问题，在输入之后加上.trim()即可解决。

总而言之，三次作业均未出现设计层面的问题，但在细节处理上不够谨慎，在日后的工程中需要更加小心，并在开发阶段做充足的鲁棒性测试。

三、分析自己发现别人bug所采用的策略

本单元的互测环节中，我主要通过黑箱测试发现bug。我首先使用了基于bash批处理的评测机，结合python的xeger库生成测试数据进行处理。但评测机的自动评测均没有出现bug，说明大家都完成了最基本的功能设计。

因此，我采用手动构造测试数据集以达到遍历样例空间的目的。手动构造的测试集无法遍历所有可能的错误，但通过率先遍历边界数据、在数据合法的范围内取各类极端值、构造数据优化的样例以找出优化漏洞的方式可以找出大多数可能存在的错误。

构造样例时，我也用到了白箱模型的思想。我将在下文结合发现其他同学的bug说明。

第一次作业

在评测机没有测出任何错误的情况下，我采用了各种极端数据和边界数据进行测试。

发现两个同学各出现一个问题。同学A在简化以-1为系数的数据时，没有删除对应的乘号。这一点可以在其代码中看出端倪：在进行优化时只做了将±1及之前可能的**删除，而没有考虑到±1可能作为求导所得结果的系数而存在。同学B出现了在项数超过300时，栈溢出的错误。（后文会对各种因正则表达式而导致的栈溢出进行分析）

第二次作业

第二次互测中，我的重要改进是使用bash脚本对互测屋内的同学实现同步测试。这样做的好处有三：输入一次样例能够得到7个人的结果，节省了很多时间。另外，通过七个人之间的结果对比很容易发现是否有人出现bug，尤其在难以化简或结果不直观时，这一方法实用性很强。对大家的优化结果进行对比也能够看出在输出优化方面所采用的的策略。我在第二次作业的讨论区详细说明了bash脚本进行批量测试的方法，欢迎大家阅读。

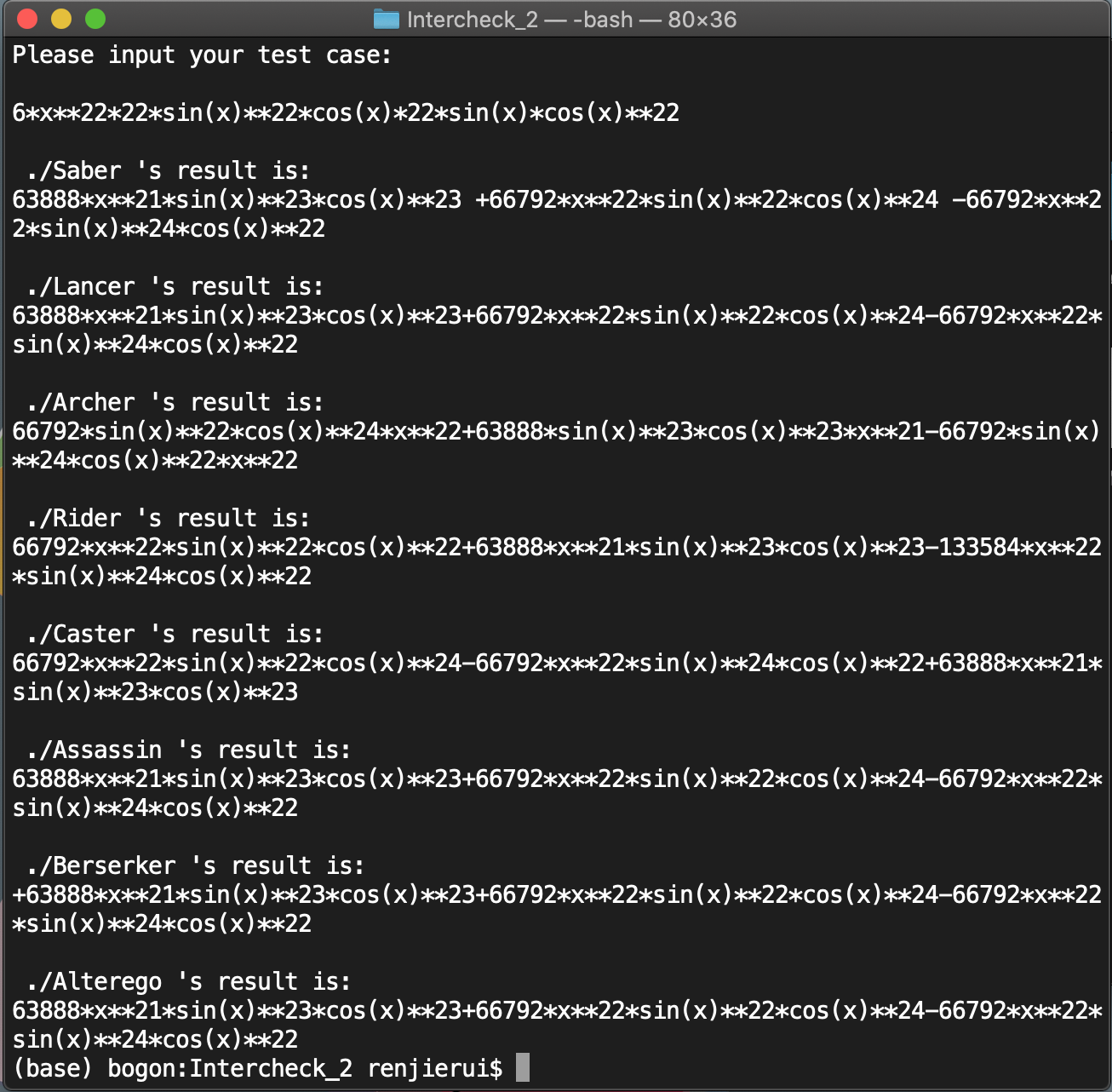
本次测试发现两个bug，同学A出现的bug为x**10000*x**10000，题目所述的“幂函数指数绝对值不超过10000”指的是输入格式，并非最终结果，这属于没有看清要求所造成的错误。同学B出现的bug为x*sin(x)**-1 + x*cos(x)**-1，和第一次作业的情况类似，在化简的过程中想当然地认为指数不可能出现-1，因为x**0求导直接得0，然而忽略了求导乘法公式的存在。

第三次作业

第三次作业中，同学们采用的实现方式多样，很难对所有人的实现细节逐一分析。但从黑箱测试的结果来看，大家的程序普遍对输入合法性的判断存在一定问题，很多同学（包括我自己）出现了不该出现的Wrong Format。说明没有对空格可能的出现位置做充分的分析，完全依赖正则表达式对正确性的判断是不可靠的。

本次测试发现诸多bug，有关输入格式判断的问题涉及很多naive的错误，在此不一一枚举。另外，有两位同学的程序出现了严重的超时问题。主要原因是使用了过大规模的正则表达式，出现了50行的正则字符串和11个Pattern类，这样进行匹配相比会出现很大问题。第二位同学和其他同学的思路有所不同，他通过主动识别错误输入的方法检测错误，而其中使用了很多.*，反复的正则回溯造成了超时问题。两位同学的代码处于隐私考虑不在此公布了。

四、应用对象创建模式

在第一次作业中，我使用了Polynomial类作为多项式类，在Polynomial类中通过new Term()语句生成所需要的Term类（项），并储存在ArrayList中。项有系数和指数两个Biginteger字段，Polynomial类依据这两个变量对项进行操作。这样的设计成功地分理出了本题的核心数据：系数和指数，但把过多的业务逻辑交给了Polynomial类，Polynomial类的方法较为复杂。

第二次作业的对象创建方式和第一次相同，类间的依赖关系也相同，只是在Term中添加了SinPow和CosPow两个字段，并分别添加了相应的化简和计算操作。

第三次作业涉及到表达式的嵌套，即因子Factor中包含表达式Expression的现象。两个类的相互调用使得上述方法不再适用。

我开始使用工厂方法模式创建对象，通过实现Factor接口完成对各种因子的统一，在SubExp表达式因子中创建Expression对象，实现表达式的递归创建。

五、对比和心得体会

我认为优秀代码都有值得我学习的以下共性：

• 代码结构清晰：优秀代码普遍对代码进行合理的分包和类的划分，类之间的耦合度很低，易于进行功能的复用和添加。我认为我在这一方面已经有所进步，但仍然需要多加练习。

• 各个类功能简单明确：优秀代码的各个类都比较精简，可以直观地看出不同模块针对的是哪一需求。这一方面我特别需要向优秀的同学学习，自己在编程时没有能够提前对需求进行充分分析，导致很多地方出现了令我自己都费解的双构造方法，倘若再没有明确的注释，代码可读性将很低。

• 命名严谨而易懂：优秀代码中的命名规则符合驼峰原则，变量名依据真实功能取英文全称，基本不会出现理解上的二义性。反观互测中出现的其他代码，虽然大体做到了按代码风格命名，但在一些不重要的变量上取名随意，出现很多诸如s1、s2的简单符号，甚至有全部使用汉语拼音做变量名的现象。我认为自己能够基本做到代码风格的严谨，但在功能添加和保持命名风格的统一方面，仍然有进步空间。

写在最后

OO编程和初学C语言有很大的不同，在完成一个小型的工程中学习各方面的知识，这可能将是在今后很长一段时间的学习和工作中我都要经历的模式。在这种情况下，原来的学习方式不再适用。一次作业的完成时间，就永远不可以预料。很多时候会因为一个小问题，一下子就耽误了很多时间，这是最痛苦的；所以说efficiency的提高对有效学习至关重要。

祝各位在今后的学习中有所进步！