多项式算法初探：从 FFT 到 NTT

注：由于发现 FWT 解决的问题和 FFT，NTT 差别有点大，加之 FMT 的存在，本文就只解决 FFT 和 NTT，剩下两个放在别的算法总结里讲。

多项式一向是算法竞赛中相当博大精深的东西，作为一个蒟蒻，我将会以最大的努力完成这篇记录，以防自己以后看不懂qwq。

---

FFT(快速傅里叶变换)

FFT 是一种可以在 \(O(n\log n)\) 的时间内完成多项式乘法的算法。这个算法的劣势在于精度。

我将会从复数、DFT、FFT 和 IFFT 四个部分完成对 FFT 的讲解。

复数

在日常的学习生活中(这是真的)，我们常会遇到一个神奇的字母：\(i\)。我们规定 \(i\) 为虚数单位，他满足 \(i^2=-1\)。

那么我们假如想要表示一个复数，我们就可以写为 \(a+bi\)，其中 \(a,b\) 为实数。前半部分我们称之为实部，后半部分我们称之为虚部。

那我们就可以开始定义虚数的运算了：

\((a+bi)+(c+di)=(a+c)+(b+d)i\)

\((a+bi)-(c+di)=(a-c)+(b-d)i\)

\((a+bi)\times(c+di)=(ac-bd)+(ad+bc)i\)

\(\dfrac{(a+bi)}{(c+di)}=\dfrac{(ac+bd)}{(c^2+d^2)}+\dfrac{(bc-ad)}{(c^2+d^2)}i\)

假如我们建立一个平面直角坐标系，横轴表示实部，纵轴表示虚部，我们就可以建立一个复平面，复平面上的每一个点都可以表示一个复数。

我们连接复平面上的点 \((a,b)\)(实际上表示复数 \(z=a+bi\))和原点，这条线段的长度即为 \(\sqrt{a^2+b^2}\)，我们称这条线段的长度为模，表示为 \(|z|\)。

那么对于一个复数 \(z=a+bi\)，我们称他的共轭复数 \(\overline{z}=a-bi\)。当 \(|z|=1\) 时，\(\overline{z}=\dfrac 1z\)。下给出证明：

\[z\times\overline{z}=(a+bi)\times(a-bi)=a^2+b^2=|z|=1
\]

在复数中，有一类数被称为单位根。若复数 \(\omega^n=1\)，我们称 \(\omega\) 为 \(n\) 次单位根。

我们如何找单位根呢？这就需要用到复平面了。我们以原点为圆心，画一个半径为 \(1\) 的圆，在满足实部正半轴是其中一条平分线的情况下将整个圆分成 \(n\) 份，每条平分线在圆上的端点所表示的复数，就是一个 \(n\) 次单位根。我们称圆与实部正半轴的交点所表示的复数(其实就是 \(1\))为 \(\omega^0_n\)，从 \(\omega^0_n\) 逆时针方向数，依次是 \(\omega^1_n,\omega^2_n,\dots,\omega^{n-1}_n\)。可以结合下面这张图理解(图片来源：https://blog.csdn.net/Flag_z/article/details/99163939)。

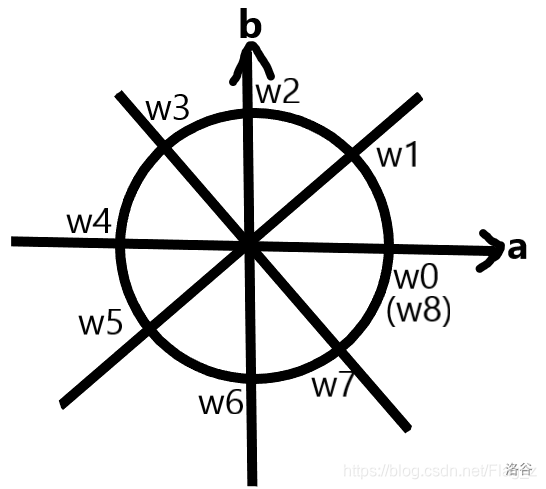
满足如下几条性质：

1. \(\omega^k_n=(\omega^1_n)^k\)
2. \(\omega^k_n=\omega^{2k}_{2n}\)
3. \(\omega^0_n=\omega^n_n\)
4. \(\omega^k_n=-\omega^{k+\frac n2}_n\)
5. \(\omega^k_n=(\cos(\frac{2\pi k}n)+(\sin(\frac{2\pi k}n))i\)
6. \(\sum\limits_{i=0}^{n-1}\omega^i_n=0\)

这些公式看上面这张图，应该都很容易推出来。

好的，复数的前置知识到此为止，接下来，我们就将进入正题。

DFT(离散傅里叶变换)

对于一个多项式 \(f(x)=\sum\limits_{i=0}^n a_ix^i\)，我们可以用 \(n\) 个不同的在这张函数图像上的点来表示。如我们选取 \(x_1,x_2,\dots,x_n\) 带入 \(f(x)\) 中，就会得到点 \((x_1,f(x_1)),(x_2,f(x_2)),\dots,(x_n,f(x_n))\)，而这些点就会对应且仅对应 \(f(x)\) 这个函数。这被称为函数的点值表示法。而从正常的多项式表达形式转化为点值表示法，时间复杂度是 \(O(n^2)\) 的。

那么，点值表示法有什么性质呢？

容易发现，对于 \(x_0\)，有 \(f(x_0)\times g(x_0)=(f\times g)(x_0)\)。这也就意味着，只要我们将两个多项式 \(f(x),g(x)\) 带入相同的 \(n\) 个 \(x\) 值，再将对应点值的 \(y\) 值相乘，再将点值表示法转化为普通形式(应该是可以拉格朗日插值做到 \(O(n^2)\) 的)，我们就完成了多项式乘法。

有什么用呢？常数甚至更大了……

此时，伟大的数学家傅里叶先生提出了离散傅里叶变换。他使用了 \(\omega^k_n\) 作为 \(x\) 值进行带入。虽然时间复杂度还是 \(n^2\)，而且常数更大了，但也为我们建立 FFT 奠定基础。

FFT(快速傅里叶变换)

我们考虑将 \(f(x)=\sum\limits_{i=0}^{n-1} a_ix^i\) 分成奇偶两个部分 \(f_0(x),f_1(x)\)(不妨设 \(n\bmod 2=0\))，满足 \(f(x)=f_0(x)+x\times f_1(x)\)，那么这两个函数就长成下面这个样子：

\[f_0(x)=\sum_{i=0}^{\frac n2-1}a_{2i}x^{2i},f_1(x)=\sum_{i=0}^{\frac n2-1}a_{2i+1}x^{2i+1}
\]

我们就把问题分成了两个部分。相当于我们求出了 \(\omega^1_{\frac 2n},\omega^2_{\frac 2n},\dots,\omega^{\frac 2n-1}_{\frac 2n}\) 的点值，现在要推导到 \(\omega^1_n,\omega^2_n,\dots,\omega^{n-1}_n\) 的点值。

那我们来推一推式子：

\[f(\omega^k_n)=f_0(\omega^{2k}_n)+\omega^k_n\times f_1(\omega^{2k}_n)
\]

\[=f_0(\omega^k_{\frac n2})+\omega^k_n\times f_1(\omega^k_{\frac n2})
\]

\[f(\omega^{k+\frac n2}_n)=f_0(\omega^{2k+n}_n)+\omega^{k+\frac n2}_n\times f_1(\omega^{2k+n}_n)
\]

\[=f_0(\omega^k_{\frac n2})-\omega^k_n\times f_1(\omega^k_{\frac n2})
\]

那这样就可以在 \(O(n)\) 的时间复杂度内推导了。这个操作有一个好听的名字，叫做蝴蝶变换。

我们使用递归分治的方法，每一层的总时间复杂度为 \(O(n)\)，一共有 \(O(\log n)\) 层，时间复杂度即为 \(O(n\log n)\)。

当然这里还有一个注意事项：考虑到每一层的 \(n\) 都得是偶数，相当于 \(n\) 必须要能表示为 \(2^x\)。考虑在前面补零即可。时间复杂度不变。

但是递归时间复杂度超大，我们难以承受。考虑采取迭代法。即我们先将单位元按照最终位置进行放置，然后从下层向上层迭代，这样常数可以小很多。

举个例子，当 \(n=8\) 时，最终形态为：

\[\omega^0_n\ \omega^4_n\ \omega^2_n\ \omega^6_n\ \omega^
1_n\ \omega^5_n\ \omega^3_n\ \omega^7_n\]

我们先把最终形态摆出来，然后再依次向上合并。

至于说具体过程，可以根据奇偶分组进行模拟。

IFFT(快速傅里叶逆变换)

我们刚才说了拉格朗日插值可以 \(O(n^2)\) 求解，但是这个思路大没前途，所以考虑深入挖掘 \(\omega\) 的性质：

当我们将 \(f(x)\) 进行 FFT 后的结果作为 \(g(x)\) 的系数，将单位根取倒数，也就是 \(\omega^0_n,\omega^{-1}_n,\dots,\omega^{1-n}_n\)。再将这些数带入 \(g(x)\) 中，进行一次快速傅里叶变换，再将所有数 \(\times\frac 1n\)，得到的就是 \(f(x)\) 的各项系数。

假如上述性质成立，那么我们只需要再做一次 FFT，就可以完成 IFFT。

下给出证明：

设 \((y_0,y_1,\dots,y_{n-1})\) 为多项式 \(f(x)=\sum\limits_{i=0}^{n-1}a_ix^i\) 的 DFT，设多项式 \(g(x)=\sum\limits_{i=0}^{n-1}y_ix^i\) 带入 \((\omega^0_n,\omega^{-1}_n,\dots,\omega^{1-n}_n)\) 的 DFT 为 \((z_0,z_1,\dots,z_{n-1})\)，则有：

\[z_k=\sum_{i=0}^{n-1}y_i(\omega^{-k}_n)^i
\]

\[=\sum_{i=0}^{n-1}(\sum_{j=0}^{n-1}a_j\times(\omega^i_n)^j)(\omega^{-k}_n)^i
\]

\[=\sum_{j=0}^{n-1}a_j\times(\sum_{i=0}^{n-1}(\omega^i_n)^{j-k})
\]

当 \(j-k=0\) 时，易得 \(\sum_{i=0}^{n-1}(\omega^i_n)^{j-k}=n\)，否则，设 \(d=\gcd(j-k,n)\)：

\[\sum_{i=0}^{n-1}(\omega^i_n)^{j-k}=\sum_{i=0}^{n-1}\omega^{(j-k)i}_n=d\sum_{i=0}^{\frac nd-1}\omega^i_{\frac nd}=0
\]

所以，\(z_k=na_k,a_k=\frac{z_k}n\)。

由于单位根的模都为 \(1\)，所以单位根的模就是他的共轭复数。

代码

下给出模板题代码：

#include<bits/stdc++.h>
using namespace std;
const int N=2097153;
const double pi=acos(-1);
int n,m,rev[N];
struct comn{double a,b;}f[N],g[N];
comn operator+(comn x,comn y){
    return {x.a+y.a,x.b+y.b};
}comn operator-(comn x,comn y){
    return {x.a-y.a,x.b-y.b};
}comn operator*(comn x,comn y){
    return {x.a*y.a-x.b*y.b,x.b*y.a+x.a*y.b};
}void operator+=(comn &x,comn y){x=x+y;}
void operator-=(comn &x,comn y){x=x-y;}
void operator*=(comn &x,comn y){x=x*y;}
void init(int k,int len){
    for(int i=0;i<len;i++)
        rev[i]=(rev[i>>1]>>1)|((i&1)<<(k-1));
}void fft(comn *a,int n,int fl){
    for(int i=0;i<n;i++)
        if(i<rev[i]) swap(a[i],a[rev[i]]);
    comn om={cos(pi),fl*sin(pi)},w={1,0};
    for(int i=1;i<n;i*=2,om={cos(pi/i),fl*sin(pi/i)})
        for(int j=0;j<n;j+=i*2,w={1,0})
            for(int k=j;k<j+i;k++){
                comn x=a[k],y=w*a[k+i];
                a[k]+=y,a[k+i]=x-y,w*=om;
            }
}int main(){
    ios::sync_with_stdio(0);
    cin.tie(0),cout.tie(0);
    cin>>n>>m;int k=0,mx=1;
    while(mx<=n+m) mx*=2,k++;
    for(int i=0;i<=n;i++) cin>>f[i].a;
    for(int i=0;i<=m;i++) cin>>g[i].a;
    init(k,mx),fft(f,mx,1),fft(g,mx,1);
    for(int i=0;i<mx;i++) f[i]*=g[i];
    fft(f,mx,-1);
    for(int i=0;i<=n+m;i++)
        cout<<(int)(f[i].a/mx+0.5)<<" ";
    return 0;
}//fast fourier transform

NTT(快速数论变换)

看似名字都变了，其实和 FFT 的基础思想差不了太多。不过系数是在取模意义下的。

考虑去掉复数，这样就不会有精度问题了。相当于我们要找到一个能够替代单位根的东西。“本是同根生，相煎何太极！”所以我们用原根炒掉单位根。

考虑上述列举的六大性质（除原第五条外），原根都能完全替代，所以直接把 FFT 模板里所有单位根改成原根，就得到了一份 NTT。

下给出代码：

#include<bits/stdc++.h>
#define int long long
using namespace std;
const int N=3e6+5;
const int p=1004535809;
int n,m,rev[N],f[N],g[N];
int qpow(int x,int y){
    int re=1;
    while(y){
        if(y&1) re=re*x%p;
        x=x*x%p,y>>=1;
    }return re;
}void init(int k,int len){
    for(int i=0;i<len;i++)
        rev[i]=(rev[i>>1]>>1)|((i&1)<<(k-1));
}void ntt(int *a,int n,int fl){
    for(int i=0;i<n;i++)
        if(i<rev[i]) swap(a[i],a[rev[i]]);
    for(int i=1;i<n;i*=2){
        int om=qpow(fl?3:(p+1)/3,(p-1)/(i<<1));
        for(int j=0,w=1;j<n;j+=i*2,w=1)
            for(int k=j;k<j+i;k++,w=w*om%p){
                int x=a[k],y=w*a[k+i]%p;
                a[k]=(x+y)%p,a[k+i]=(x-y+p)%p;
            }
    }
}signed main(){
    ios::sync_with_stdio(0);
    cin.tie(0),cout.tie(0);
    cin>>n>>m;int k=0,mx=1;
    while(mx<=n+m) mx*=2,k++;
    for(int i=0;i<=n;i++) cin>>f[i];
    for(int i=0;i<=m;i++) cin>>g[i];
    init(k,mx),ntt(f,mx,1),ntt(g,mx,1);
    for(int i=0;i<mx;i++) f[i]=(f[i]*g[i])%p;
    ntt(f,mx,0);int qp=qpow(mx,p-2);
    for(int i=0;i<=n+m;i++)
        cout<<f[i]*qp%p<<" ";
    return 0;
}//fast fourier transform