[Machine Learning] 单变量线性回归(Linear Regression with One Variable) - 线性回归-代价函数-梯度下降法-学习率

单变量线性回归(Linear Regression with One Variable)

　　什么是线性回归？线性回归是利用数理统计中回归分析，来确定两种或两种以上变量间相互依赖的定量关系的一种统计分析方法(取自 百度百科)。

　　例如：现在有一堆散乱的点，想找出一个一元一次方程来让这些点的分布误差最小(就是找出一条最合适的直线来贯穿这些点)。

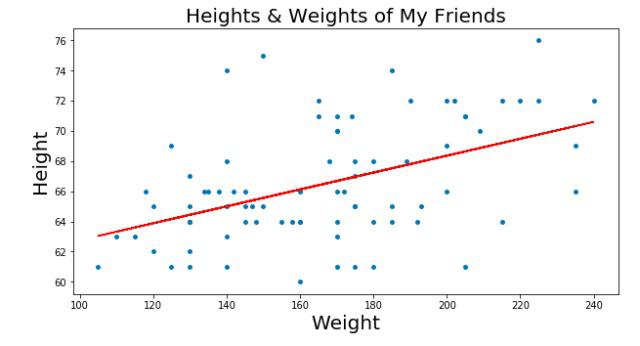
图中红色直线就是我们需要找的线。这条直线的表示为: y=ax+b。那么找出a、b这两个变量最合适的值就叫线性回归。

在图片中，蓝色的点用(xi,yi)来表示。m代表所有点的数量。我们的目的就是找出y=ax+b这个直线，实际上就是找出a、b这两个值。

那么如何判断a、b的值是我们需要的呢？我们先假设a、b的值为θ1、θ0，那么假设的直线就为h(x)=θ0+θ1x.我们可以计算所有点到直线的平方误差值来评判是否接近a、b的值。

（图中右式应该再除以 m.）

J(θ) 就表示平方误差，同时J(θ) 也是代价函数。

我们可以不停的给θ1、θ0取值，找出代价函数在所有θ1、θ0情况下最小的值，那么此时的θ1、θ0 就是我们需要找的a、b.

如何来调整θ1、θ0的取值来寻找a、b的值呢？这个时候就需要使用梯度下降法。

梯度下降是一个用来求函数最小值的算法。最直观的方法就是对代价函数求导，来找出J(θ) 的最小值。但是，我们需要的不是最小值，是最小值与之对应的θ1、θ0的值。所有我们对J(θ)求偏导，来获取θ1、θ0的值。

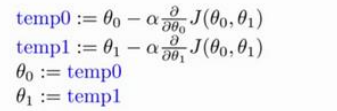
求θ的方法就是：新的θ = θ - θ的偏导*比例。

这里的比例表示的是减小值的缩放，如果没有这个值的话，假设偏导结果很大，那么执行减法的时候就有可能使得新的θ减了一个比正确值大很多的数，从而无法获取正确的值，所以即使减小的步骤多一些也要保证可以获取到正确的结果。

同时这里的比例也叫学习率，同时也是梯度下降法的梯度。