【ybt高效进阶2-4-3】【luogu P4551】最长异或路径

最长异或路径

题目链接：ybt高效进阶2-4-3 / luogu P4551

题目大意

给定一棵 n 个点的带权树，结点下标从 1 开始到 N。寻找树中找两个结点，求最长的异或路径。

异或路径指的是指两个结点之间唯一路径上的所有边权的异或。

思路

首先看到要异或的值最大，我们要想到可以用 Trie 树来贪心弄。

但是它好像不知道怎么弄，那我们先不管它。

那我们看到是一棵树，那我们可以试着统计 \(i\) 到根节点（我这里设是 \(1\)）的异或路径的长度是多少。

那我们考虑能不能用这个表示出任意两个点之间的异或路径。

这里先给出结论，其实就是两个点到根节点的异或路径异或起来得出的值。

我们来证明：

分两种情况，分别是一个点在另一个点到根节点的路径上，要么就是两条路径是分开的，不会相交。

1. 第一种，那我们可以知道一个点，就是一个值异或它自己就是 \(0\)，就会消掉。那你想想，第一种情况时这个图：
   
   
   
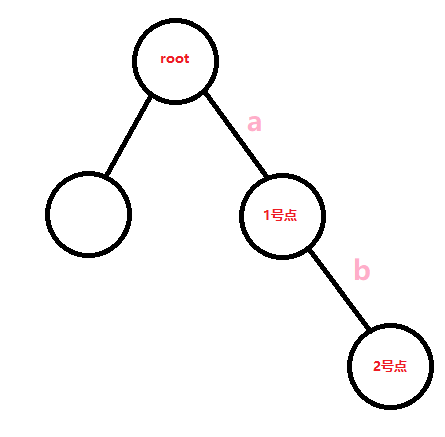
   那 \(1\) 号点到根节点的异或路径就是 \(a\)，\(2\) 号点到根节点的异或路径是 \(a\oplus b\)，我们要的是 \(b\)。
   
   那你发现，把它们异或起来，就是 \(a\oplus a\oplus b=b\)。（两个 \(a\) 异或起来抵消掉了）
2. 第二种，那我们可以画图。
   
   
   
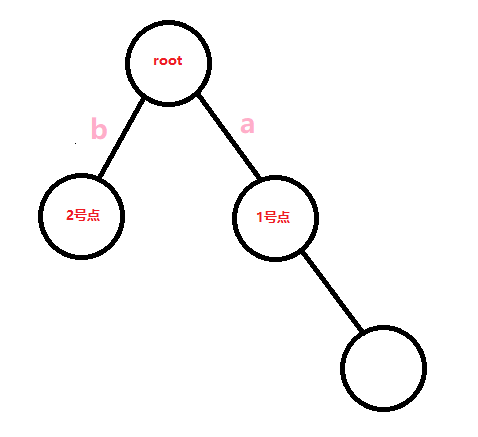
   那 \(1\) 号点到根节点的异或路径就是 \(a\)，\(2\) 号点到根节点的异或路径是 \(b\)，我们要的是 \(a\oplus b\)。
   
   那你发现，把它们异或起来，就是 \(a\oplus b\)。

那你就可以一开始预处理出到根节点的异或路径，然后枚举两个点，然后算这两个点的异或路径，然后取最大值。

但是很明显这样是 \(O(n^2)\) 的，它会超时。

那我们就想一想有什么方法可以快速求最大值的。

想想我们之前一开始想用什么方法？

没错，就是 Trie 树。

我们可以把每个点到根节点的异或路径都放进 Trie 树里面构造。

然后每次枚举你要的异或路径的另一个点，然后跟 Trie 树里面的路径匹配找到最大值。

前面做过一题就是求这个最大值的，主要的就是用了贪心的思想。

从高位向低位枚举，然后如果有跟你这一位不同的就优先选，同时统计这一位异或之后是 \(1\) 对数的贡献。然后如果没有不同的，就看有没有相同的。

（因为毕竟你可以这一位相同，然后尽可能让后面更高的位不同，这样的贡献就更大）

那如果想相同不相同都没有，那就只能以当前的贡献退出了。

（如果想看之前的那一题可以点我查看，不过我只写在了 csdn，博客园里没有，因为比较简单）

然后对这些最大值选一个最大的，就是答案了。

代码

#include<cstdio>
#include<iostream>

using namespace std;

struct node {
	int x, to, nxt;
}e[200001];
struct Tree {
	int son[2];
}trie[1000001];
int n, x, y, z, le[100001], KK, go, KKK, ans;

void add(int x, int y, int z) {//邻接表
	e[++KK] = {z, y, le[x]}; le[x] = KK;
	e[++KK] = {z, x, le[y]}; le[y] = KK;
}

void build(int num) {//Trie树建树
	int now = 0;
	for (int i = 31; i >= 0; i--) {
		go = num >> i & 1;
		if (!trie[now].son[go]) trie[now].son[go] = ++KKK;
		now = trie[now].son[go];
	}
}

int find(int num) {
	int now = 0, re = 0;
	for (int i = 31; i >= 0; i--) {//从高位到低位贪心看
		go = num >> i & 1;
		if (trie[now].son[go ^ 1]) {//先看能不能有这一位不同
			now = trie[now].son[go ^ 1];
			re |= 1 << i;
		}
		else if (trie[now].son[go]) now = trie[now].son[go];//只能相同
			else return re;//都没有，就只能退出了
	}
	return re;
}

void dfs1(int now, int father, int num) {//建出从根节点到 i 点的异或路径构成的 Trie 数
	build(num);
	for (int i = le[now]; i; i = e[i].nxt)
		if (e[i].to != father)
			dfs1(e[i].to, now, num ^ e[i].x);
}

void dfs2(int now, int father, int num) {//得出与现在的路径异或能得到的最大值
	ans = max(ans, find(num));
	for (int i = le[now]; i; i = e[i].nxt)
		if (e[i].to != father)
			dfs2(e[i].to, now, num ^ e[i].x);
}

int main() {
	scanf("%d", &n);
	for (int i = 1; i < n; i++) {
		scanf("%d %d %d", &x, &y, &z);
		add(x, y, z);
	}

	dfs1(1, 0, 0);

	dfs2(1, 0, 0);

	printf("%d", ans);

	return 0;
}