[NOI2003]逃学的小孩 （贪心+树的直径+暴力枚举）

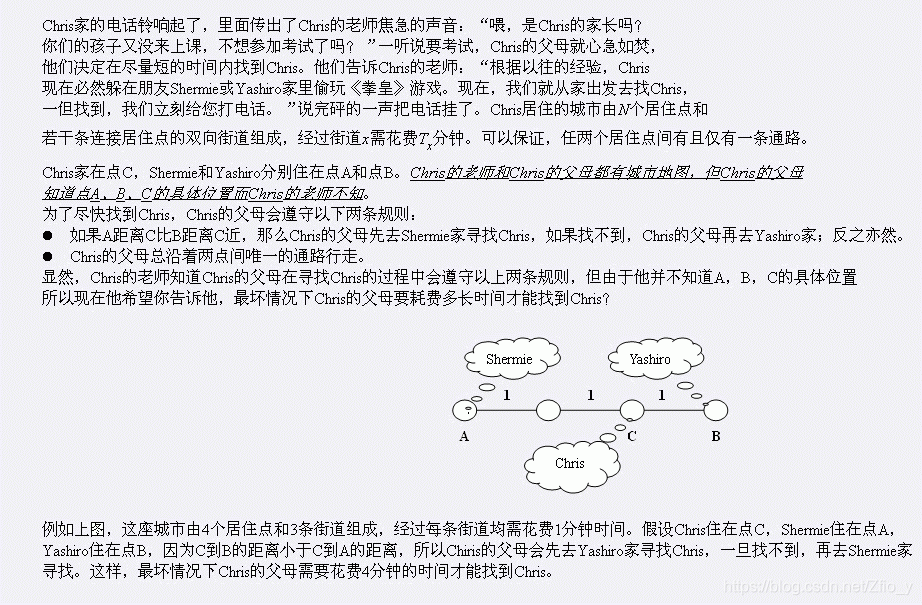
Input

第一行是两个整数N（3 <= N <= 200000）和M，分别表示居住点总数和街道总数。以下M行，每行给出一条街道的信息。第i+1行包含整数Ui、Vi、Ti（1<=Ui, Vi <= N，1 <= Ti <= 1000000000），表示街道i连接居住点Ui和Vi，并且经过街道i需花费Ti分钟。街道信息不会重复给出。

Output

仅包含整数T，即最坏情况下Chris的父母需要花费T分钟才能找到Chris。

输入输出样例

Intput:

4 3

1 2 1

2 3 1

3 4 1

Output:

4

开脑洞的时间到了：

花里胡哨的题干感觉是这题最难的地方了...

又是追捕又是搜查的，抓个逃课搞得跟缉毒一样(我也想逃课啊)

回归正题，从题目中给的描述中我们很容易能知道这是一棵树，还是双向的。

因为A和B的位置不确定(这也代表A、B只是象征性的，我们可以随意互换A、B的位置)，为了让用时最长肯定让A和B离的最远，说白了就是要找到树的直径

关于贪心的合理性证明可以参见洛谷：传送门

A、B的用时最远了，我们还需要让出发点C最远，思路很明朗，在遍历时直接记录下每个点到A跟B的距离即可(前提是知道A和B，我们要先遍历一遍找到A跟B，再把数组清零重新遍历找距离)

找到所有的距离后，那么最后的答案就是：取每个点中到A或B的距离中较小的那一个距离(每个点应该有两个距离，到A一个、到B一个，我们取较小的那个)，再在每个取出来的距离中取一个最大值，再加上直径，即为答案 (为什么要选较小的那个呢？题目要求我们先去离的近的那家) ，这句话我自己单看都绕不太懂，可以结合下面的代码看一看，能自己画个图模拟一下就更好了(下面给出了两种输出方案，但本质是一样的，都是我上边解释的这种，形式上方案2比较好理解)

（另外，不要忘记开long long...能全开就全开吧，我就是有的变量开了long long 有的没开结果翻了车...）

#include<cstdio>
#include<cstring>
#include<iostream>
#include<algorithm>
using namespace std;
const int maxn=200000+10;
#define ll long long
ll dis_A[maxn],dis_B[maxn],head[maxn],len=0;
ll zhijing=0;
int n,m,B,A;//这里的A、B只是个相对的概念，象征着直径的两端，毕竟题目中的A、B本身就可以互换
struct Edge{
    int next,to,dis;
}edge[maxn<<1];
void Add(int a,int b,int c){
    edge[++len].dis=c;
    edge[len].to=b;
    edge[len].next=head[a];
    head[a]=len;
}
void Find_A(int u,int fa,int flag){//这个函数是用来找到每个点到A点的距离的
    for(int i=head[u];i;i=edge[i].next){
        int v=edge[i].to,w=edge[i].dis;
        if(v==fa) continue;
        dis_A[v]=dis_A[u]+w;
        if(flag){ //我们手动设计一个开关，只有第一遍的时候我们才需要找到B，但实际上不加这个if应该没什么影响
            if(dis_A[v]>dis_A[B]) B=v;
        }
        Find_A(v,u,flag);
    }
}
void Find_B(int u,int fa,int flag){//同上，只不过要找的点变为另一端
    for(int i=head[u];i;i=edge[i].next){
        int v=edge[i].to,w=edge[i].dis;
        if(v==fa)continue;
        dis_B[v]=dis_B[u]+w;
        if(flag) {
            if(dis_B[v]>dis_B[A]) {
                A=v;
                zhijing=dis_B[v];
            }
        }
        Find_B(v,u,flag);
    }
}
int main(){
    memset(dis_A,0,sizeof(dis_A));
    memset(dis_B,0,sizeof(dis_B));
    cin>>n>>m;
    for(int i=1;i<=m;i++){
        int u,v,w;
        scanf("%d%d%d",&u,&v,&w);
        Add(u,v,w),Add(v,u,w);
    }
    Find_A(1,0,true);//第一遍遍历，我们要找到点A，也就是树的直径的一端
    Find_B(B,0,true);//我们以找到的一端进行遍历，找到直径的另一端
    ll ans=dis_B[A];//dis_B[A]其实就是直径,如果不明白可以取消掉下面的注释看一看

    //printf("dis_A[B]=%d dis_B[B]=%d zhijing=%d\n",dis_A[B],dis_B[B],zhijing);

    memset(dis_A,0,sizeof(dis_A));//这里一定要归零，因为我们要重新计算距离
    memset(dis_B,0,sizeof(dis_B));
    Find_A(B,0,false);
    Find_B(A,0,false);

    //输出方案1
    /*ll cc=0;
    for(int i=1;i<=n;i++){
        ll d=min(dis_B[i],dis_A[i]);
        if(d>cc) cc=d;
    }
    cout<<ans+cc<<endl;
    */

    //输出方案2
    /*
    ll ans2=-999999999999;
    for(int i=1;i<=n;i++){
        ans2=max(ans2,min(dis_A[i],dis_B[i]));
    }
    cout<<ans2+zhijing<<endl;
    */

    return 0;
}