Benelux Algorithm Programming Contest 2014 Final（第二场）

B:Button Bashing

You recently acquired a new microwave, and noticed that it provides a large number of buttons to be able to quickly specify the time that the microwave should be running for. There are buttons both for adding time, and for subtracting time. You wonder how efficient you can be when entering cooking times: you want to minimize the number of required button presses.

The microwave can be running for at least 0 seconds, and at most 1 hour. If a button press would result in a cooking time of less than 0 seconds, the microwave will set the cooking time to 0 seconds. If a button press would result in a cooking time of more than 1 hour, the microwave will set the cooking time to 1 hour. Initially, the microwave will run for 0 seconds. There will always be a button adding at least 1 second to the cooking time.

Given the buttons that the microwave provides for entering cooking times, determine the least amount of button presses required to let the microwave run for a certain amount of time. If it is not possible to enter the desired cooking time precisely, determine the smallest achievable cooking time above the target, and the minimum number of button presses required for that cooking time, instead. The microwave does not allow to adjust the cooking time once it has started cooking.

Input Format

On the first line one positive number: the number of test cases, at most 100. After that per test case:

one line with two space-separated integers n and t (1≤n≤16,0≤t≤3600): the number of buttons available to change the cooking time, and the desired cooking time in seconds, respectively.
one line with n space-separated integers bi (−3600≤bi≤3600): the number of seconds added to the cooking time when button iii is pressed.

Output Format

Per test case:

one line with two space-separated integers: the minimum number of button presses required to reach the required cooking time, and the minimum number of extra seconds that the microwave must be running for, respectively.

样例输入

样例输出

2 0

3 10
不够0秒作为0秒处理，超过3600秒当做3600秒处理，是一个背包问题，要求的是在超过m最小的情况下，按的字数最小

#include <iostream>

#include <algorithm>

#include <cstring>

#include <cstdio>

#include <vector>

#include <queue>

#include <stack>

#include <cstdlib>

#include <iomanip>

#include <cmath>

#include <cassert>

#include <ctime>

#include <map>

#include <set>

using namespace std;

#pragma comment(linker, "/stck:1024000000,1024000000")

#define lowbit(x) (x&(-x))

#define max(x,y) (x>=y?x:y)

#define min(x,y) (x<=y?x:y)

#define MAX 100000000000000000

#define MOD 1000

#define pi acos(-1.0)

#define ei exp(1)

#define PI 3.1415926535897932384626433832

#define ios() ios::sync_with_stdio(true)

#define INF 0x3f3f3f3f

#define mem(a) (memset(a,0,sizeof(a)))

typedef long long ll;

int t,n,m,a[],dp[<<];

struct node

{

    int step,time;

}ans,pos,cnt,inf;

int main()

{

    scanf("%d",&t);

    while(t--)

    {

        scanf("%d%d",&n,&m);

        for(int i=;i<=n;i++)

            scanf("%d",&a[i]);

        memset(dp,INF,sizeof(dp));

        dp[]=;

        queue<node>q;

        pos.step=,pos.time=;

        ans.step=INF,ans.time=INF;

        q.push(pos);

        while(!q.empty())

        {

            pos=q.front();

            q.pop();

            if(pos.time>=m)

            {

                if(ans.time>pos.time) ans=pos;

                else if(ans.time==pos.time && ans.step>pos.step) ans=pos;

            }

            for(int i=;i<=n;i++)

            {

                int nex=pos.time+a[i];

                if(nex<) nex=;

                if(nex>) nex=;

                if(dp[nex]>=INF)

                {

                    dp[nex]=dp[pos.time]+;

                    cnt.step=dp[nex];

                    cnt.time=nex;

                    q.push(cnt);

                }

            }

        }

        printf("%d %d\n",ans.step,ans.time-m);

    }

    return ;

}

G:Growling Gears

The Best Acceleration Production Company specializes in multi-gear engines. The performance of an engine in a certain gear, measured in the amount of torque produced, is not constant: the amount of torque depends on the RPM of the engine. This relationship can be described using a torque-RPM curve.

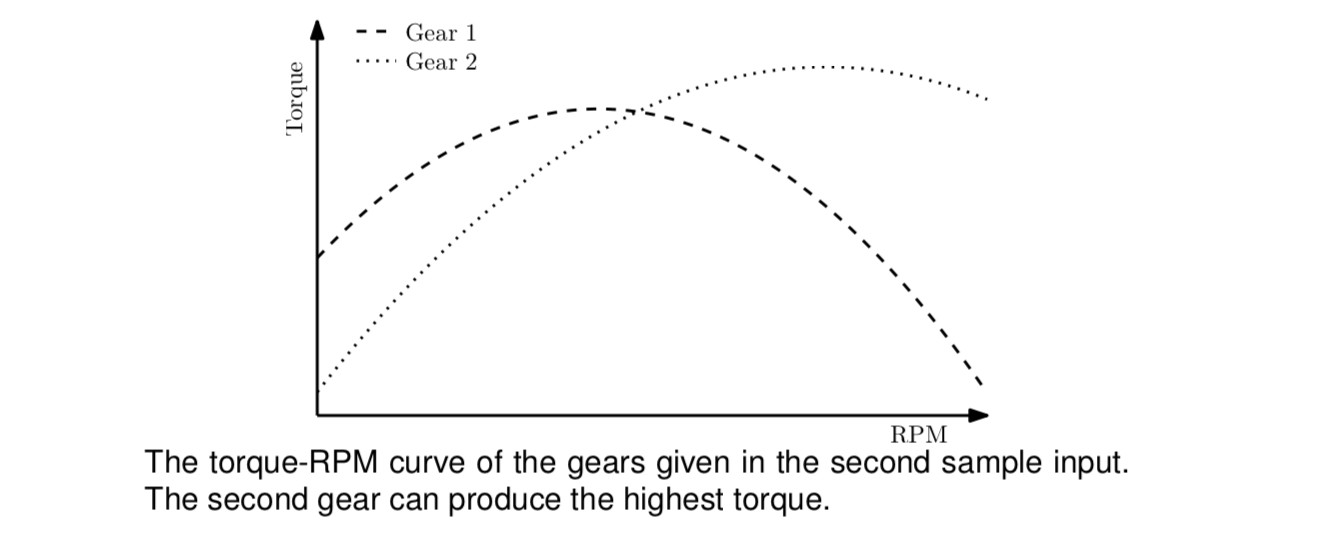
For the latest line of engines, the torque-RPM curve of all gears in the engine is a parabola of the form T=−aR2+bR+c,where R is the RPM of the engine,and T is the resulting torque.

Given the parabolas describing all gears in an engine, determine the gear in which the highest torque is produced. The first gear is gear 1, the second gear is gear 2, etc. There will be only one gear that produces the highest torque: all test cases are such that the maximum torque is at least 1 higher than the maximum torque in all the other gears.

Input Format

On the first line one positive number: the number of test cases, at most 100. After that per test case:

one line with a single integer n (1≤n≤10): the number of gears in the engine.
n lines, each with three space-separated integers a, b and c (1≤a,b,c≤104): the parameters of the parabola T=−aR2+bR+c describing the torque-RPM curve of each engine.

Output Format

Per test case:

one line with a single integer: the gear in which the maximum torque is generated.

样例输入

样例输出

1

2

2
数学问题，求给定方程的最大顶点

#include <iostream>

#include <algorithm>

#include <cstring>

#include <cstdio>

#include <vector>

#include <queue>

#include <stack>

#include <cstdlib>

#include <iomanip>

#include <cmath>

#include <cassert>

#include <ctime>

#include <map>

#include <set>

using namespace std;

#pragma comment(linker, "/stck:1024000000,1024000000")

#define lowbit(x) (x&(-x))

#define max(x,y) (x>=y?x:y)

#define min(x,y) (x<=y?x:y)

#define MAX 100000000000000000

#define MOD 1000

#define pi acos(-1.0)

#define ei exp(1)

#define PI 3.1415926535897932384626433832

#define ios() ios::sync_with_stdio(true)

#define inf 0x3f3f3f3f

#define mem(a) (memset(a,0,sizeof(a)))

typedef long long ll;

int t,n;

int main()

{

    scanf("%d",&t);

    while(t--)

    {

        scanf("%d",&n);

        double ans;

        int pos=;

        for(int i=,a,b,c;i<n;i++)

        {

            scanf("%d%d%d",&a,&b,&c);

            double x=-*a*c-b*b;

            double y=-*a;

            if(i==) ans=x/y;

            else if(ans<x/y)

            {

                ans=x/y;

                pos=i;

            }

        }

        printf("%d\n",pos+);

    }

    return ;

}

I:Interesting Integers

Undoubtedly you know of the Fibonacci numbers. Starting with F1=1 and F2=1,every next number is the sum of the two previous ones. This results in the sequence 1,1,2,3,5,8,13,⋅⋅⋅

Now let us consider more generally sequences that obey the same recursion relation

Gi=Gi−1+Gi−2 for i>2

but start with two numbers G1≤G2of our own choice. We shall call these Gabonacci sequences. For example, if one uses G1=1 and G2=3, one gets what are known as the Lucas numbers: 1,3,4,7,11,18,29,⋅⋅⋅ . These numbers are – apart from 1 and 3 – different from the Fibonacci numbers.

By choosing the first two numbers appropriately, you can get any number you like to appear in the Gabonacci sequence. For example, the number n appears in the sequence that starts with 1 and n−1, but that is a bit lame. It would be more fun to start with numbers that are as small as possible, would you not agree?

Input Format

On the first line one positive number: the number of test cases, at most 100. After that per test case:

one line with a single integer n (2≤n≤109): the number to appear in the sequence.

Output Format

Per test case:

one line with two integers a and b (0<a≤b),such that,for G1 and G2=b,Gk= for some k. These numbers should be the smallest possible, i.e., there should be no numbers a and b′ with the same property, for which b′<b, or for which b′=b and a′<a.

样例输入

样例输出

首先可以退出时任意组合，所以根据斐波那契数列，可得af[i-1]+b[f[i-2]=n,解即可

#include <iostream>

#include <algorithm>

#include <cstring>

#include <cstdio>

#include <vector>

#include <queue>

#include <stack>

#include <cstdlib>

#include <iomanip>

#include <cmath>

#include <cassert>

#include <ctime>

#include <map>

#include <set>

using namespace std;

#pragma comment(linker, "/stck:1024000000,1024000000")

#define lowbit(x) (x&(-x))

#define max(x,y) (x>=y?x:y)

#define min(x,y) (x<=y?x:y)

#define MAX 100000000000000000

#define MOD 1000

#define pi acos(-1.0)

#define ei exp(1)

#define PI 3.1415926535897932384626433832

#define ios() ios::sync_with_stdio(true)

#define INF 0x3f3f3f3f

#define mem(a) (memset(a,0,sizeof(a)))

typedef long long ll;

ll n,fic[],t;

void init()

{

    fic[]=,fic[]=;

    for(int i=;i<=;i++)

        fic[i]=fic[i-]+fic[i-];

}

ll exgcd(ll a,ll b,ll &x,ll &y)

{

    if(b==){

        x=;

        y=;

        return a;

    }

    ll tmp=exgcd(b,a%b,y,x);

    y=y-(a/b)*x;

    return tmp;

}

int main()

{

    init();

    scanf("%lld",&t);

    while(t--)

    {

        scanf("%lld",&n);

        ll l=,r=n;

        for(int i=;i<=;i++)

        {

            if(fic[i]>n) break;

            ll x,y;

            ll tmp=exgcd(fic[i-],fic[i-],x,y);

            x*=n;

            y*=n;

            ll ans=(y-x)/fic[i];

            x+=ans*fic[i-];

            y-=ans*fic[i-];

            if(x>y) x-=fic[i-],y+=fic[i-];

            if(x<= || y<=) continue;

            if(r>y) r=y,l=x;

            else if(r==y && l>x) l=x;

        }

        printf("%lld %lld\n",l,r);

    }

    return ;

}

J：Jury Jeopardy

What would a programming contest be without a problem featuring an ASCII-maze? Do not despair: one of the judges has designed such a problem.

The problem is about a maze that has exactly one entrance/exit, contains no cycles and has no empty space that is completely enclosed by walls. A robot is sent in to explore the entire maze. The robot always faces the direction it travels in. At every step, the robot will try to turn right. If there is a wall there, it will attempt to go forward instead. If that is not possible, it will try to turn left. If all three directions are unavailable, it will turn back.

The challenge for the contestants is to write a program that describes the path of the robot, starting from the entrance/exit square until it finally comes back to it. The movements are described by a single letter: 'F' means forward, 'L' is left, 'R' is right and 'B' stands for backward.Each of 'L', 'R' and 'B' does not only describe the change in orientation of the robot, but also the advancement of one square in that direction. The robot's initial direction is East. In addition, the path of the robot always ends at the entrance/exit square.

The judge responsible for the problem had completed all the samples and testdata, when disaster struck: the input file got deleted and there is no way to recover it! Fortunately the output and the samples are still there. Can you reconstruct the input from the output? For your convenience, he has manually added the number of test cases to both the sample output and the testdata output.

Input Format

On the first line one positive number: the number of test cases. After that per test case:

one line with a single string: the movements of the robot through the maze.

Output Format

On the first line one positive number: the number of test cases, at most 100. After that per test case:

one line with two space-separated integers h and w (3≤h,w≤100): the height and width of the maze, respectively.
h lines, each with w characters, describing the maze: a '#' indicates a wall and a '.' represents an empty square.

The entire contour of the maze consists of walls, with the exception of one square on the left: this is the entrance. The maze contains no cycles (i.e. paths that would lead the robot back to a square it had left in another direction) and no empty squares that cannot be reached from the entrance. Every row or column – with the exception of the top row, bottom row and right column – contains at least one empty square.

样例输入

3

FFRBLF

FFRFRBRFBFRBRFLF

FRLFFFLBRFFFRFFFRFRFBRFLBRFRLFLFFR

样例输出

3

4 4

####

...#

##.#

####

7 5

#####

...##

##.##

#...#

##.##

##.##

#####

7 7

#######

#...#.#

#.#...#

#.#.###

..###.#

#.....#

#######

模拟题。

#include <iostream>

#include <algorithm>

#include <cstring>

#include <cstdio>

#include <vector>

#include <queue>

#include <stack>

#include <cstdlib>

#include <iomanip>

#include <cmath>

#include <cassert>

#include <ctime>

#include <map>

#include <set>

using namespace std;

#pragma comment(linker, "/stck:1024000000,1024000000")

#define lowbit(x) (x&(-x))

#define max(x,y) (x>=y?x:y)

#define min(x,y) (x<=y?x:y)

#define MAX 100000000000000000

#define MOD 1000

#define pi acos(-1.0)

#define ei exp(1)

#define PI 3.1415926535897932384626433832

#define ios() ios::sync_with_stdio(true)

#define INF 0x3f3f3f3f

#define mem(a) (memset(a,0,sizeof(a)))

typedef long long ll;

int a[][],t;

string s;

int main()

{

    scanf("%d",&t);

    printf("%d\n",t);

    while(t--)

    {

        cin>>s;

        memset(a,,sizeof(a));

        int k=s.size();

        int row=,col=,visl=,visr=,visu=,visd=;

        int ok=;

        a[row][col]=;

        for(int i=;i<k;i++)

        {

            if(s[i]=='F')

            {

                if(ok==) col+=;

                else if(ok==) row+=;

                else if(ok==) col-=;

                else if(ok==) row-=;

                ok=(ok+)%;

            }

            if(s[i]=='R')

            {

                if(ok==) row+=;

                if(ok==) col-=;

                if(ok==) row-=;

                if(ok==) col+=;

                ok=(ok+)%;

            }

            if(s[i]=='L')

            {

                if(ok==) row-=;

                if(ok==) col+=;

                if(ok==) row+=;

                if(ok==) col-=;

                ok=(ok+)%;

            }

            if(s[i]=='B')

            {

                if(ok==) col-=;

                if(ok==) row-=;

                if(ok==) col+=;

                if(ok==) row+=;

                ok=(ok+)%;

            }

            a[row][col]=;

            visl=min(visl,col);

            visr=max(visr,col);

            visu=min(visu,row);

            visd=max(visd,row);

        }

        visu--,visd++,visr++;

        printf("%d %d\n",visd-visu+,visr-visl+);

        for(int i=visu;i<=visd;i++)

        {

            for(int j=visl;j<=visr;j++)

                printf("%c",a[i][j]?'.':'#');

            printf("\n");

        }

    }

    return ;

}