每天进步一点点-深度学习入门-基于Python的理论与实现 （2）

今天要补上两天的

不补了，新手，看的比较慢--

---

手写识别例子跳过先

思考如何实现数字5的识别

三种方法：

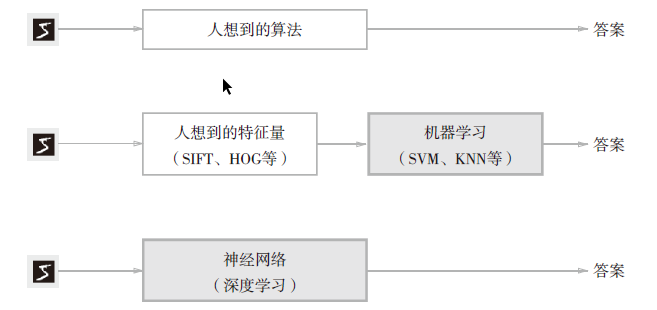
训练数据：学习，寻找最优解

测试数据：评价模型能力.

损失函数：以损失函数为线索寻找自由权重参数，讲解损失函数：https://blog.csdn.net/qq_24753293/article/details/78788844

mini-batch学习：机器学习就是是针对训练数据计算损失函数的值，找出使该值尽可能小的参数，所以如果训练数据有100 个的话，我们就要把这100 个损失函数的总和作为学习的指标。

为何要设定损失函数而不使用目标精度作为指标：关键在于导数不为0，如果以对精度求导，大多数地方导数为0，无法根据导数变化更新值

（具体为啥大多数地方对精度求导会得0我理解的不是很清楚..

书中说的是，值得细微变化并不会引起精度的变化

我理解就是值得变化对于精度不敏感，当值变化很多时，精度才会变化一点，此时需要一个敏感的损失函数，值的每一点变化都能时刻反应值的这一点增减对于损失函数的走向，由此再次细微调节值，两者相互敏感的变化。

好像就这样：损失函数是一个能表达精度又能对值变化敏感（导数敏感）的函数。

）

例1：损失函数为均方误差

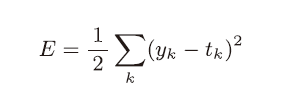
import numpy as np

#均方误差会计算神经网络的输出和正确解监督数据的各个元素之差的平方，再求总和。

# 经过训练后，出现0-9的期望

y=[0.1,0.05,0.6,0.0,0.05,0.1,0.0,0.1,0.0,0.0]

# 训练后的期望与实际期望的差值进行一定运算，其值越小越准确

def mean_squared_error(y,t):

​ return 0.5*np.sum((y-t)**2)

# 测试数据，测试数据结果为2,即实际期望

t=[0,0,1,0,0,0,0,0,0,0]

print(mean_squared_error(np.array(y),np.array(t)))

# 测试数据，测试数据结果为7,即实际期望

t=[0,0,0,0,0,0,1,0,0,0]

print(mean_squared_error(np.array(y),np.array(t)))