http://www.riaway.com/

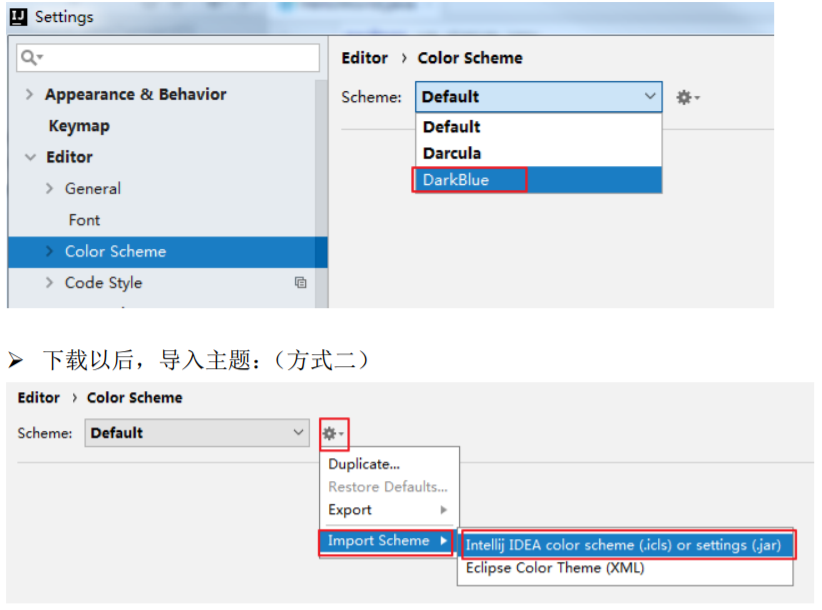
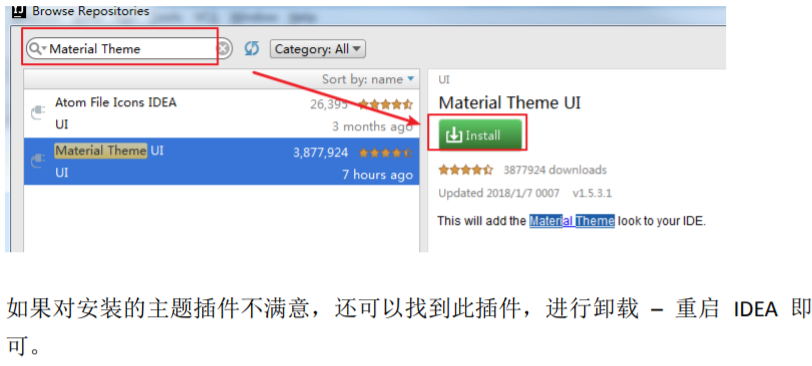
IntelliJ IDEA 2017.3尚硅谷-----主题的更多相关文章

  1. IntelliJ IDEA 2017.3尚硅谷-----修改当前主题字体、字体大小、行间距、控制台、注释

  2. IntelliJ IDEA 2017.3尚硅谷-----插件的使用

    在 IntelliJ IDEA 的安装讲解中我们其实已经知道,IntelliJ IDEA 本身很多功能也都 是通过插件的方式来实现的.官网插件库:https://plugins.jetbrains.c ...

  3. IntelliJ IDEA 2017.3尚硅谷-----取消更新

  4. IntelliJ IDEA 2017.3尚硅谷-----缓存和索引的清理

  5. IntelliJ IDEA 2017.3尚硅谷-----生成 javadoc

    Locale:输入语言类型:zh_CN Other command line arguments:-encoding UTF-8 -charset UTF-8

  6. IntelliJ IDEA 2017.3尚硅谷-----配置 Maven

  7. IntelliJ IDEA 2017.3尚硅谷-----断点调试

  8. IntelliJ IDEA 2017.3尚硅谷-----版本控制(Version Control)

    不管是个人开发还是团队开发,版本控制都会被使用.而 IDEA 也很好的集成了 版本控制的相关结构. Git 的 msysGit 官网下载:https://git-scm.com/ Git 客户端 To ...

  9. IntelliJ IDEA 2017.3尚硅谷-----关联数据库

随机推荐

  1. 在source insight project中删除文件夹或者文件的通用方法

    1.删除文件夹或者文件在硬盘上的数据 2.project->synchronize files...看到如下图,然后勾选remove missing files from project

  2. 【Unity|C#】基础篇(18)——正则表达式（Regex类）

    [学习资料] <C#图解教程>:https://www.cnblogs.com/moonache/p/7687551.html 电子书下载:https://pan.baidu.com/s/ ...

  3. 洛谷P1219 八皇后 我。。。。。。

    代码1    (学弟版) #include<bits/stdc++.h>using namespace std;int l[15];bool s[15];                  ...

  4. 51Nod 1182 完美字符串 （贪心）

    约翰认为字符串的完美度等于它里面所有字母的完美度之和.每个字母的完美度可以由你来分配,不同字母的完美度不同,分别对应一个1-26之间的整数. 约翰不在乎字母大小写.(也就是说字母F和f)的完美度相同. ...

  5. IDEA模板注释及相关快捷键设置

    IDEA模板注释及相关快捷键设置 最近使用IDEA时发现自带的模板注释不怎么好用,因此自己根据网上的教程总结了适合自己的模板设置,可以一键生成类和方法的注释,废话不多说一起看看吧: 第9步的类模板注释 ...

  6. lampp ERROR 1044 (42000): Access denied for user ''@'localhost' to database 'lepus'

    解决方法: 在[mysqlld]段下增加如下代码:skip-grant-tables: 1.which mysql 查看mysql位置,例如:/opt/lampp/bin/mysql 2.进入配置my ...

  7. Selenium3+python自动化013-自动化数据驱动及模型介绍

    一.查看当前运行的浏览等相关信息 driver=webdriver.Chrome() print(driver.capabilities["version"]) #浏览器版本 pr ...

  8. Python里的Flask开发环境的搭建

    在已经安装好了Python后,我这里用的是Python3.5,准备进一步学习Flask框架,下面记录搭建Flask环境 这里使用了虚拟环境,在虚拟环境里,最小化的安装Flask. 参考步骤: 1.首先 ...

  9. AntDesign(React)学习-2 第一个页面

    1.前面创建了第一个项目jgdemo,结构如下,使用TypeScript. 2.yarn start启动项目 3.点击GettingStarted是umi的官方网站 https://umijs.org ...

  10. jQuery---学习roadmap---4 parts

    jQuery---学习roadmap---4 parts jQuery初识 jQuery让js的开发变得更加简单 jQuery解决了浏览器的兼容性问题 学习目标 使用jQuery设计常见的效果 掌握j ...