DFA与NFA的等价性,DFA化简
等价性
对于每个NFA M存在一个DFA M’,使得L(M)=L(M’)--------等价性证明,NFA的确定化
假定NFA M=<S, Σ, δ, S 0 , F>,我们对M的状态转换图进行以下改造:

解决初始状态唯一性:引进新的初态结点X和终态结点Y,X,Y∉S,从X到S 0中任意状态结点连一条ε箭弧, 从F中任意状态结点连一条ε箭弧到Y
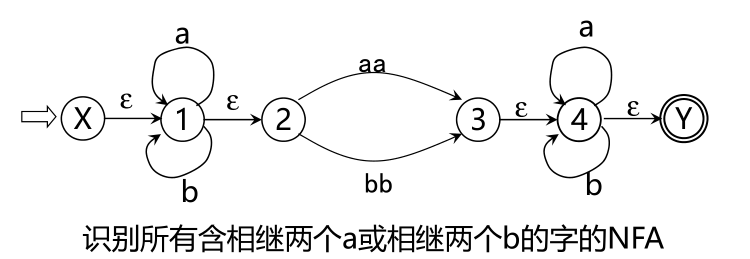
简化弧上的标记:对M的状态转换图进一步施行替换,其中k是新引入的状态

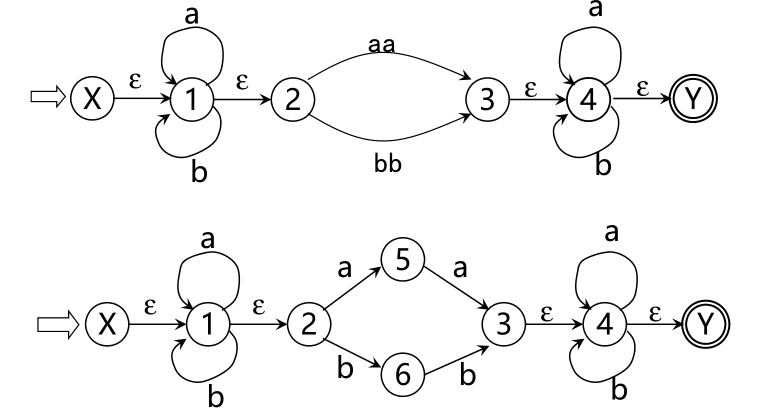
逐步把这个图转变为每条弧只标记为Σ上的一个字符或ε,最后得到一个NFA M’,显然L(M’)=L(M)

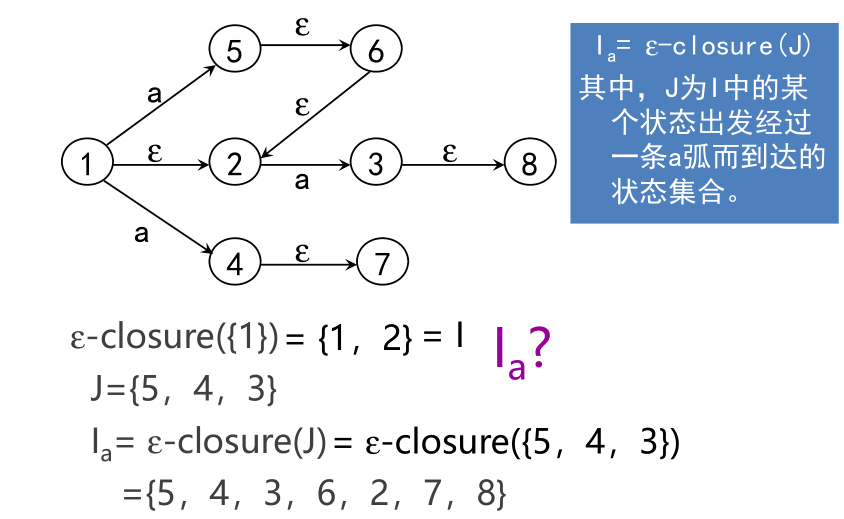

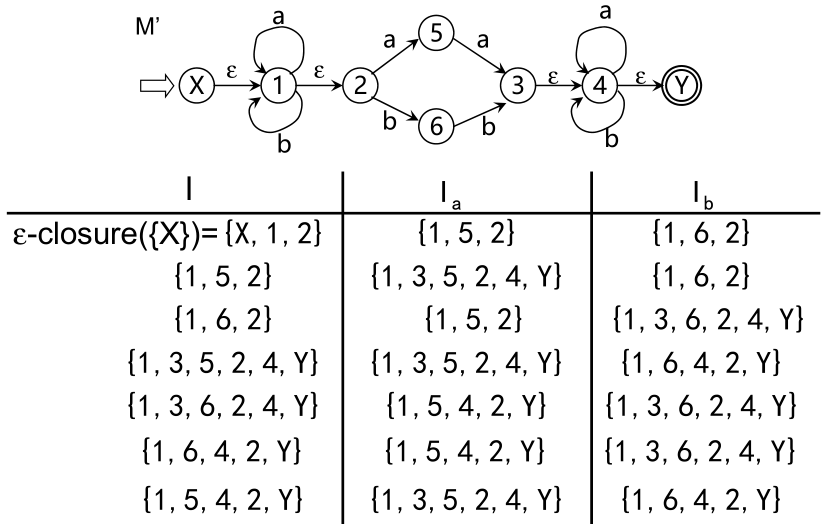
把表看成状态转换矩阵,子集视为状态,转换表唯一刻划了一个确定的有限自动机M,初态是ε-closure({X}),终态是含有原终态Y的子集,不难看出,这个DFA M与M’等价对于每个NFA M存在一个DFA M ’ ,使得 L(M)=L(M’),NFA和DFA等价

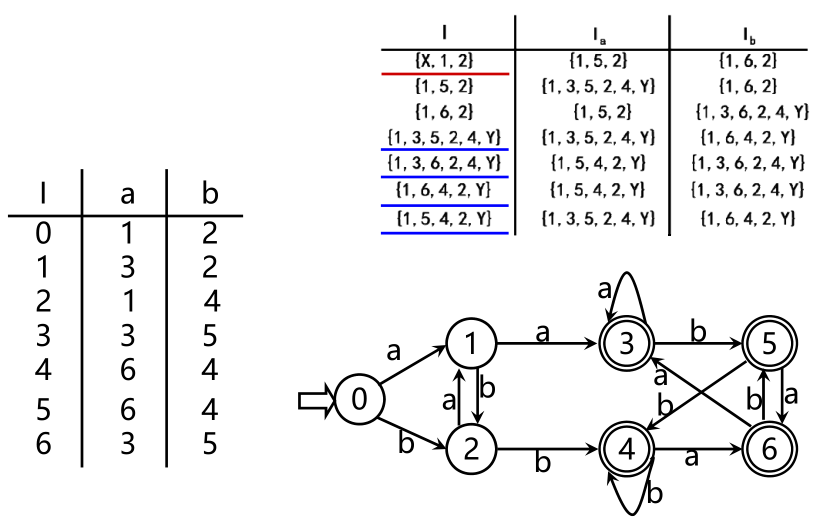
确定有限自动机的化简
对于给定的DFA M,寻找一个状态数比M少的DFAM’,使得L(M)=L(M’),假设s和t为M的两个状态,称s和t等价:如果从状态s出发能读出某个字α而停止于终态,那么同样,从t出发也能读出α而停止于终,两个状态不等价,则称它们是可区别的态;反之亦然
基本思想
把M的状态集划分为一些不相交的子集,使得任何两个不同子集的状态是可区别的,而同一子集的任何两个状态是等价的, 最后,让每个子集选出一个代表,同时消去其他状态。
对DFA的状态集合S进行第一次划分,正确的分法是:终态和非终态
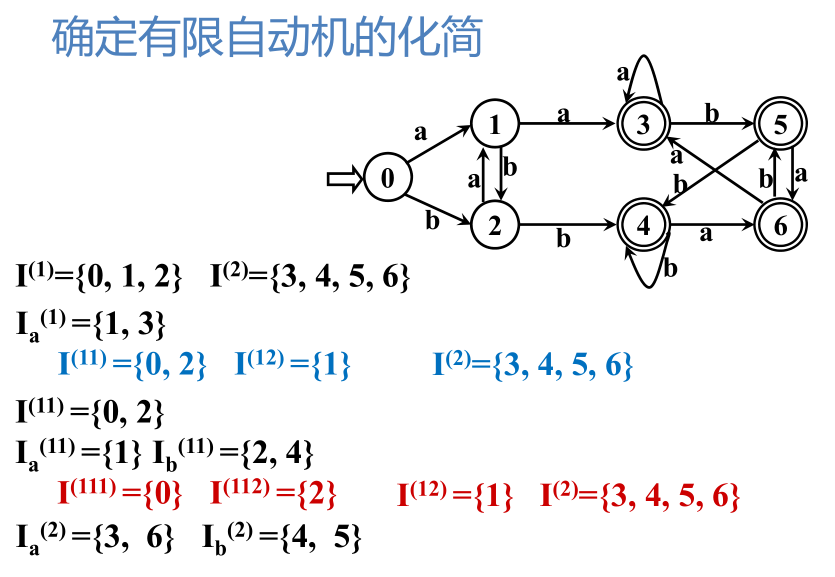
{0} {1} {2} {3, 4, 5, 6}
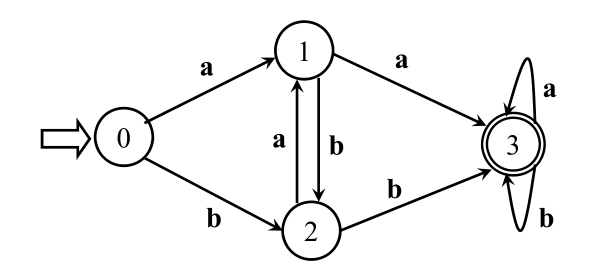


DFA与NFA的等价性,DFA化简的更多相关文章
- NFA转换为等价的DFA
在编译系统中,词法分析阶段是整个编译系统的基础.对于单词的识别,有限自动机FA是一种十分有效的工具.有限自动机由其映射f是否为单值而分为确定的有限自动机DFA和非确定的有限自动机NFA.在非确定的有限 ...
- 正规式与正规集,DFA与NFA
词法分析器的设计 词法分析器的功能:输入源程序.输出单词符号 词法分析器的设计:给出程序设计语言的单词规范--单词表, 对照单词表设计识别该语言所有单词的状态转换图, 根据状态转换图编写词法分析程序 ...
- DFA化简
首先是未化简DFA的转换表 NFA状态 DFA状态 a b {0,1,2,4,7} A B C {1,2,3,4,6,7,8} B B D {1,2,4,5,6,7} C B C {1,2,4,5,6 ...
- 《编译原理》构造与正规式 (0|1)*01 等价的 DFA - 例题解析
<编译原理>构造与正规式 (0|1)*01 等价的 DFA - 例题解析 解题步骤: NFA 状态转换图 子集法 DFA 的状态转换矩阵 DFA 的状态转图 解: 已给正规式:(0|1)* ...
- 编译原理-DFA的化简(最小化)
对于给定的DFA M,寻找一个状态数比M小的DFA M'使得L(M)=L(M') 1.状态的等价性: 假设s和t为M的两个状态 ①若分别从状态s和状态t出发都能读出某个字α而停止于终态,则 ...
- 编译原理实验 NFA子集法构造DFA,DFA的识别 c++11实现
实验内容 将非确定性有限状态自动机通过子集法构造确定性有限状态自动机. 实验步骤 1,读入NFA状态.注意最后需要设置终止状态. 2,初始态取空,构造DFA的l0状态,将l0加入未标记状态队列que ...
- DFA和NFA的区别
正则表达式引擎分成两类,一类称为DFA(确定性有穷自动机),另一类称为NFA(非确定性有穷自动机).两类引擎要顺利工作,都必须有一个正则式和一个文本串,一个捏在手里,一个吃下去.DFA捏着文本串去比较 ...
- NNs(Neural Networks,神经网络)和Polynomial Regression(多项式回归)等价性之思考,以及深度模型可解释性原理研究与案例
1. Main Point 0x1:行文框架 第二章:我们会分别介绍NNs神经网络和PR多项式回归各自的定义和应用场景. 第三章:讨论NNs和PR在数学公式上的等价性,NNs和PR是两个等价的理论方法 ...
- 2020-BUAA OO-面向对象设计与构造-HW11中对ageVar采用缓存优化的等价性证明(包括溢出情况)
HW11中对ageVar采用缓存优化的等价性证明(包括溢出情况) 概要 我们知道,第三次作业里age上限变为2000,而如果缓存年龄的平方和,2000*2000*800 > 2147483647 ...
随机推荐
- xlwings excel(二)
常用函数和方法 Book 工作簿常用的apiwb=xw.books[‘工作簿名称'] wb.activate()激活为当前工作簿 wb.fullname 返回工作簿的绝对路径 wb.name 返回工作 ...
- 学习 lind 语 里的一些组件使用。
step one autofac : link:http://files.cnblogs.com/files/ganmk--jy/AutofacTest.rar step two 还有很多
- FluentData -Micro ORM with a fluent API that makes it simple to query a database
Code samples Create and initialize a DbContextThe connection string on the DbContext class can be in ...
- 《Netlogo多主体建模入门》笔记 2
从自带的模型库开始 财富分配模型 黄色代表稻谷,有的人消化快,有的慢,稻谷的积累代表财富的积累,不涉及交易行为. 点击setup后 ,点击 go 红线--穷人: 绿线-- 中产 : 蓝 ...
- SpringCloud学习之搭建eureka集群,手把手教学,新手教程
一.为什么需要集群 上一篇文章讲解了如何搭建单个节点的eureka,这篇讲解如何搭建eureka集群,这里的集群还是本地不同的端口执行三个eureka,因为条件不要允许,没有三台电脑,所以大家将就一下 ...
- HTTP负责均衡模块(HTTP Upstream)
这个模块为后端的服务器提供简单的负载均衡(轮询(round-robin)和连接IP(client IP))如下例: upstream backend { server backend1.examp ...
- Linux基础:简介安装、常用命令和JDK、Mysql、Tomcat的安装
一.Linux的简介 1.Linux的概述 Linux是基于Unix的开源免费的操作系统,由于系统的稳定性和安全性几乎成为程序代码运行的最佳系统环境.Linux是由Linus Torvalds(林纳斯 ...
- ogg trail文件序列号不一致
一.Cause 在某些情况下,对于一个已经running的OGG进程,对已同步的数据(正确的同步或者错误的同步)做修改,修改完之后,需要保持一个一致点,从一致点继续同步. 这时需要人工干涉产生一个新的 ...
- 在Centos上安装docker,部署mysql数据库
何为docker? Docker 可以让开发者打包他们的应用以及依赖包到一个轻量级.可移植的容器中,然后发布到任何流行的 Linux 机器上,也可以实现虚拟化. 本机环境 24小时不关机的Centos ...
- Spring注入bean的方式
在Spring容器中为一个bean配置依赖注入有三种方式: · 使用属性的setter方法注入 这是最常用的方式: · 使用构造器注入: · 使用Filed注入(用于注解方式). 使用属性的se ...
