HDU 4568 Hunter（最短路径+DP）（2013 ACM-ICPC长沙赛区全国邀请赛）

Problem Description

　　One day, a hunter named James went to a mysterious area to find the treasures. James wanted to research the area and brought all treasures that he could.
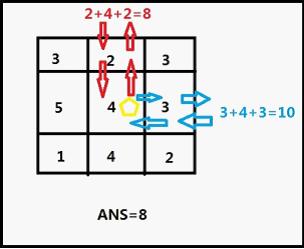
　　The area can be represented as a N*M rectangle. Any points of the rectangle is a number means the cost of research it,-1 means James can't cross it, James can start at any place out of the rectangle, and explore point next by next. He will move in the rectangle and bring out all treasures he can take. Of course, he will end at any border to go out of rectangle(James will research every point at anytime he cross because he can't remember whether the point are researched or not).
　　Now give you a map of the area, you must calculate the least cost that James bring out all treasures he can take(one point up to only one treasure).Also, if nothing James can get, please output 0.

 

Input

　　The input consists of T test cases. The number of test cases T is given in the first line of the input. Each test case begins with a line containing 2 integers N M , (1<=N,M<=200), that represents the rectangle. Each of the following N lines contains M numbers(0~9),represent the cost of each point. Next is K(1<=K<=13),and next K lines, each line contains 2 integers x y means the position of the treasures, x means row and start from 0, y means column start from 0 too.

 

Output

　　For each test case, you should output only a number means the minimum cost.

 

题目大意：一个n*m的格子，每个格子有一个花费cost，如果花费是-1代表格子不能走。现在格子里有K个宝藏，问拿齐K个宝藏的最小花费，只能进出一次。

思路：首先，注意到K很小，还是一个很奇葩的数字。所以，其实这题的路径就是要走遍这K个点的最短路，这就是经典的TSP问题，位DP解决。需要预处理出每个点到其他点的最短路径，把矩阵外看成一个点（在我的代码里标号为K），对每个点做单源最短路径即可。

PS：这题有说，如果拿不到任何宝藏输出0，其实这条件是没用的……这题的描述有一点坑爹，如果你有一些宝藏能拿到，有一些宝藏不能拿到（被一堆-1围着），那我要输出啥？经测试根本就没有这种东西……因为都是有答案的所以根本就不需要考虑宝藏所在点是-1和点点之间不连通这种坑爹的问题了。

PS2：我做这题的时候没看到-1，然后Dijkstra+heap不断MLE，后来加了个vis判是否出队的问题，就WA了……之前一直没想明白为什么会出现MLE的情况，看来是-1加了进去有无穷多的数进队导致……

 

代码（171MS）：

 #include <cstdio>
 #include <queue>
 #include <utility>
 #include <iostream>
 #include <cstring>
 using namespace std;
 typedef pair<int, int> PII;

 const int MAXN = ;

 int mat[MAXN][MAXN], tx[], ty[];
 int dis[MAXN][MAXN], di[][];
 bool ist[MAXN][MAXN];
 int post[MAXN][MAXN];
 int n, m, k;

 #define pos(x, y) (x*MAXN+y)

 int fx[] = {-,,,};
 int fy[] = {,,,-};

 void min_path(int st_x, int st_y, int now) {
     priority_queue<PII> que;
     que.push(make_pair(-mat[st_x][st_y], pos(st_x, st_y)));
     memset(dis, 0x3f, sizeof(dis));
     dis[st_x][st_y] = mat[st_x][st_y];
     while(!que.empty()) {
         int abc = -que.top().first, tmp = que.top().second; que.pop();
         int x = tmp / MAXN, y = tmp % MAXN;
         if(abc != dis[x][y]) continue;
         for(int i = ; i < ; ++i) {
             int newx = x + fx[i], newy = y + fy[i];
             if( <= newx && newx < n &&  <= newy && newy < m) {
                 if(mat[newx][newy] == -) continue;
                 if(dis[newx][newy] > mat[newx][newy] + dis[x][y]) {
                     dis[newx][newy] = mat[newx][newy] + dis[x][y];
                     que.push(make_pair(-dis[newx][newy], pos(newx, newy)));
                     if(ist[newx][newy] && dis[newx][newy] < di[now][post[newx][newy]])
                         di[now][post[newx][newy]] = dis[newx][newy];
                 }
             }
             else if(dis[x][y] < di[now][k]) di[now][k] = dis[x][y];
         }
     }
 }

 int dp[][];
 int ans, sum;

 int dfs(int u, int use) {
     if(dp[u][use] < 0x3f3f3f3f) return dp[u][use];
     if(use == ) {
         return dp[u][use] = di[u][k];
     }
     for(int i = ; i < k; ++i) {
         if(use & ( << i))
             dp[u][use] = min(dp[u][use], di[u][i] + dfs(i, use ^ ( << i)));
     }
     return dp[u][use];
 }

 void solve() {
     memset(dp, 0x3f, sizeof(dp));
     ans = 0x7fff7fff;
     for(int i = ; i < k; ++i)
         ans = min(ans, di[i][k] + dfs(i, ( << i) ^ (( << k) - )));
 }

 void printdi() {
     for(int i = ; i < k; ++i) {
         for(int j = ; j <= k; ++j) printf("%d ", di[i][j]);
         printf("\n");
     }
 }

 int main() {
     int T;
     scanf("%d", &T);
     while(T--) {
         scanf("%d%d", &n, &m);
         for(int i = ; i < n; ++i)
             for(int j = ; j < m; ++j) scanf("%d", &mat[i][j]);
         scanf("%d", &k);
         memset(ist, , sizeof(ist));
         sum = ;
         for(int i = ; i < k; ++i) {
             scanf("%d%d", &tx[i], &ty[i]);
             ist[tx[i]][ty[i]] = true;
             post[tx[i]][ty[i]] = i;
             sum += mat[tx[i]][ty[i]];
         }
         memset(di, 0x3f, sizeof(di));
         for(int i = ; i < k; ++i) min_path(tx[i], ty[i], i);
         //printdi();
         solve();
         printf("%d\n", ans - sum);
     }
 }