FDR错误发现率-P值校正学习[转载]

1.定义

FDR（false discovery rate），是统计学中常见的一个名词，翻译为伪发现率，其意义为是错误拒绝（拒绝真的（原）假设）的个数占所有被拒绝的原假设个数的比例的期望值。

//FDR是个期望值

2.利用Benjamini–Hochberg方法计算FDR的计算及R语言实现

FDR的计算相当简单，包括以下几步：

1.对p值进行从小到大的排序，标记上序号1~n；

2.其中，最大的FDR(不考虑重复则为第n位)等于最大的p值；

3.对于n-1位的FDR，取下面两者的较小值：

上一步(第n位)计算得出的FDR值；
p值*n/(n-1)

4.不断迭代第三步(n-2,n-3....)，直至计算到最小p值对应的FDR。

例子：

temp <-c(0.01,0.11,0.21,0.31,0.41,0.51,0.61,0.71,0.81,0.91)

p.adjust(temp,method = "fdr")

结果：

[] 0.1000000 0.5500000 0.7000000 0.7750000 0.8200000 0.8500000 0.8714286

 [] 0.8875000 0.9000000 0.9100000

另外，如果对temp的倒数第二个P值进行更改：

temp2 <-c(0.01,0.11,0.21,0.31,0.41,0.51,0.61,0.71,0.90,0.91)

p.adjust(temp2,method = "fdr")

[] 0.1000000 0.5500000 0.7000000 0.7750000 0.8200000 0.8500000 0.8714286

[] 0.8875000 0.9100000 0.9100000

第一次：min(0.91,0.81*10/9)=0.90

第二次：min(0.91,0.90*10/9)=0.91

分别演示了两个取到不同值的过程。

这样可以保证从统计学上FDP不超过q。

3.确定FDR

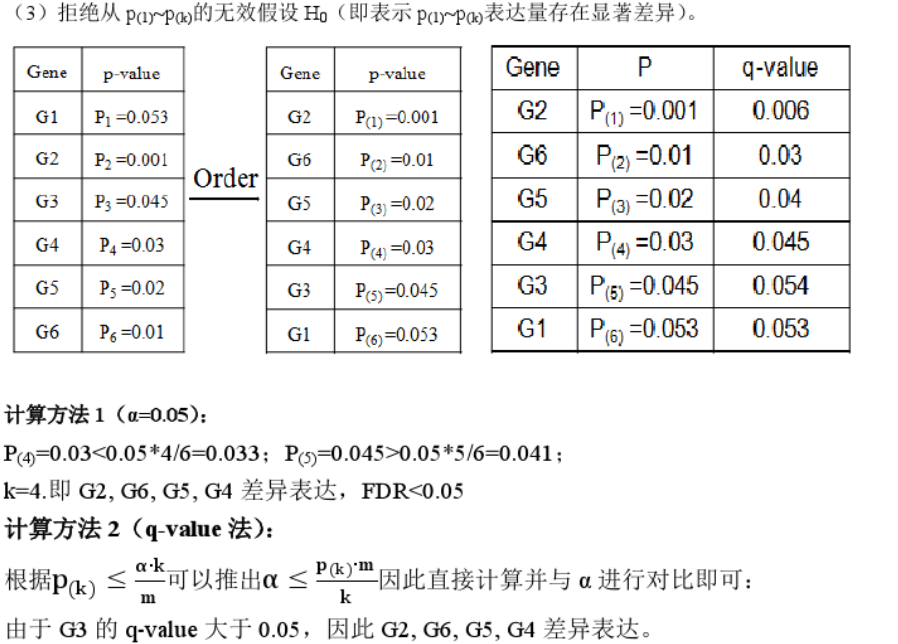
3.只使用P值的话

单次检验：针对单个基因（蛋白），采用统计检验，假设采用的p值为小于0.05，我们通常认为这个基因在两个（组）样本中的表达是有显著差异的，但是仍旧有5%的概率，这个基因并不是差异基因。

注：原假设是两个基因不存在显著性差异。

多次检验：当两个（组）样本中有10000个基因采用同样的检验方式进行统计检验时，这个时候就有一个问题，单次犯错的概率为0.05，进行10000次检验的话，那么就有0.05*10000=500 个基因的差异被错误估计了。

有一种严格校正法：

Bonferroni 校正法
Bonferroni校正法：如果进行N次检验，那么p值的筛选的阈值设定为p/N。比如，进行10000次检验的话，如果p值选择为0.05，那么校正的p值筛选为0.000005。 p值低于此的基因才是显著性差异基因。
该方法虽然简单，但是过于严格，导致最后找的差异基因很少，甚至找不到差异的基因。

4.假设检验

我们在处理宏基因组差异基因的选择时，需要对两个样本的每个基因进行一次假设检验。如果我们有m个基因，那么我们就要做m次假设检验。每一次的假设检验的零假设H0为：两个样本的这个基因没有显著性差异。其中有m0个零假设是正确的，即这个基因在两个样本中确实没有显著性差异；但有m1=m-m0个零假设是错误的，即两个样本的这个基因是有显著性差异。m次检验之后，被拒绝的零假设的个数记为R。为了方便记忆，可用一张表格来表示假设检验的结果，如上。

我们可以得到FDR准则，即要求控制错误拒绝率。令Q=V / (V+S)，它表示被错误拒绝的零假设数目占所有被拒绝的零假设数目的比例。Q也是一个不可观测的随机变量。

https://stackoverflow.com/questions/10323817/r-unexpected-results-from-p-adjust-fdr

这个里讲了如何计算及过程，明天来总结。

5.R中的cummin函数

> cummin(c(:, :, :))

[]         

> c(:, :, :)

[]         

#求从左到右累积的最小值。

#到第二个2出现时已经有了最小值是1，所以对应都是1.

#到第一个0出现时，是最小值，那么对应之后再出现的4   累计最小值都是0.