logistic回归和softmax回归
logistic:二分类
softmax:多分类
logistic回归
在 logistic 回归中,我们的训练集由 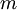 个已标记的样本构成:
个已标记的样本构成: 。由于 logistic 回归是针对二分类问题的,因此类标记
。由于 logistic 回归是针对二分类问题的,因此类标记 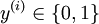 。
。
假设函数(hypothesis function): 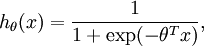
代价函数(损失函数):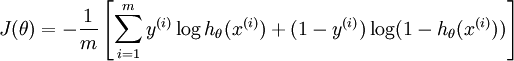
我们的目标是训练模型参数 ,使其能够最小化代价函数。
,使其能够最小化代价函数。
假设函数就相当于我们在线性回归中要拟合的直线函数。
softmax回归
在 softmax回归中,我们的训练集由 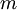 个已标记的样本构成:
个已标记的样本构成: 。由于softmax回归是针对多分类问题(相对于 logistic 回归针对二分类问题),因此类标记
。由于softmax回归是针对多分类问题(相对于 logistic 回归针对二分类问题),因此类标记  可以取
可以取  个不同的值(而不是 2 个)。我们有
个不同的值(而不是 2 个)。我们有 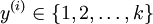 。
。
对于给定的测试输入  ,我们想用假设函数针对每一个类别j估算出概率值
,我们想用假设函数针对每一个类别j估算出概率值 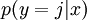 。也就是说,我们想估计
。也就是说,我们想估计  的每一种分类结果出现的概率。因此,我们的假设函数将要输出一个
的每一种分类结果出现的概率。因此,我们的假设函数将要输出一个  维的向量(向量元素的和为1)来表示这
维的向量(向量元素的和为1)来表示这  个估计的概率值。 具体地说,我们的假设函数
个估计的概率值。 具体地说,我们的假设函数 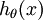 形式如下:
形式如下:
- 假设函数:
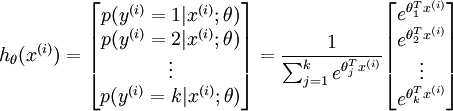
- 其中
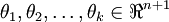 是模型的参数。请注意
是模型的参数。请注意 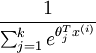 这一项对概率分布进行归一化,使得所有概率之和为 1 。
这一项对概率分布进行归一化,使得所有概率之和为 1 。 -
为了方便起见,我们同样使用符号
 来表示全部的模型参数。在实现Softmax回归时,将
来表示全部的模型参数。在实现Softmax回归时,将  用一个
用一个 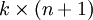 的矩阵来表示会很方便,该矩阵是将
的矩阵来表示会很方便,该矩阵是将 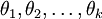 按行罗列起来得到的,如下所示:
按行罗列起来得到的,如下所示:
也就是说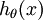 表示的是x属于不同类别的概率组成的向量。
表示的是x属于不同类别的概率组成的向量。
- 代价函数:
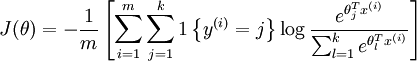
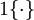 是示性函数,其取值规则为
是示性函数,其取值规则为
值为真的表达式
值得注意的是,logistic回归代价函数是softmax代价函数的特殊情况。因此,logistic回归代价函数可以改为:
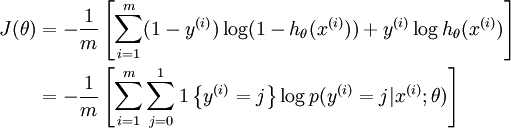
- 一点个人理解:
-
为什么二分类中参数只有一个
 ,而k分类中参数却有k个。
,而k分类中参数却有k个。 -
其实二分类中的
 是y=1情况下的参数,而y=0情况下其实未给出参数,因为y=0的假设函数值可以通过1-(y=1的假设函数值)得到。同理,k分类中参数其实只需要k-1个参数就可以了,多余的一个参数是冗余的。
是y=1情况下的参数,而y=0情况下其实未给出参数,因为y=0的假设函数值可以通过1-(y=1的假设函数值)得到。同理,k分类中参数其实只需要k-1个参数就可以了,多余的一个参数是冗余的。
具体冗余参数有什么负面影响,参考Softmax回归 http://ufldl.stanford.edu/wiki/index.php/Softmax%E5%9B%9E%E5%BD%92
logistic回归和softmax回归的更多相关文章
- 线性回归、Logistic回归、Softmax回归
线性回归(Linear Regression) 什么是回归? 给定一些数据,{(x1,y1),(x2,y2)…(xn,yn) },x的值来预测y的值,通常地,y的值是连续的就是回归问题,y的值是离散的 ...
- 1.线性回归、Logistic回归、Softmax回归
本次回归章节的思维导图版总结已经总结完毕,但自我感觉不甚理想.不知道是模型太简单还是由于自己本身的原因,总结出来的东西感觉很少,好像知识点都覆盖上了,但乍一看,好像又什么都没有.不管怎样,算是一次尝试 ...
- Machine Learning 学习笔记 (3) —— 泊松回归与Softmax回归
本系列文章允许转载,转载请保留全文! [请先阅读][说明&总目录]http://www.cnblogs.com/tbcaaa8/p/4415055.html 1. 泊松回归 (Poisson ...
- 机器学习 —— 基础整理(五)线性回归;二项Logistic回归;Softmax回归及其梯度推导;广义线性模型
本文简单整理了以下内容: (一)线性回归 (二)二分类:二项Logistic回归 (三)多分类:Softmax回归 (四)广义线性模型 闲话:二项Logistic回归是我去年入门机器学习时学的第一个模 ...
- 机器学习(三)—线性回归、逻辑回归、Softmax回归 的区别
1.什么是回归? 是一种监督学习方式,用于预测输入变量和输出变量之间的关系,等价于函数拟合,选择一条函数曲线使其更好的拟合已知数据且更好的预测未知数据. 2.线性回归 于一个一般的线性模型而言,其 ...
- DNN:逻辑回归与 SoftMax 回归方法
UFLDL Tutorial 翻译系列:http://deeplearning.stanford.edu/wiki/index.php/UFLDL_Tutorial 第四章:SoftMax回归 简介: ...
- 广义线性模型------逻辑回归和softmax回归
1.广义线性模型 2.逻辑回归 3.softmax回归
- DeepLearning之路(二)SoftMax回归
Softmax回归 1. softmax回归模型 softmax回归模型是logistic回归模型在多分类问题上的扩展(logistic回归解决的是二分类问题). 对于训练集,有. 对于给定的测试 ...
- softmax回归---sigmoid(1)
介绍softmax之前先讲讲sigmoid: 逻辑回归模型常用的函数:sigmoid函数(用来做二分类) 表达式:f(x)=L/(1+exp-k(x-x0)) 其图像: 本质:将一个真值映射到(0,1 ...
随机推荐
- ResourceManager High Availability
Introduction This guide provides an overview of High Availability of YARN’s ResourceManager, and det ...
- 对爱奇艺PC Web主站来说,良好的SEO能够帮助其获得更多的搜索流量,因而页面上一些非常重要的内容仍然需要依靠服务端进行渲染,由于另外开发一套基于Node的SSR后台成本较高,而乐趣(基于java和velocity模板引擎)平台作为渲染系统已经十分成熟且运行稳定,在充分试验后,我们决定在Uniqy中使用服务端同步与客户端浏览器异步二次渲染相结合的方式,结合Vue2.0提供的 slot插槽机制,很
https://mp.weixin.qq.com/s/eB20BoqzENO_oNk8eDg4Eg 干货|爱奇艺PC Web新框架实践 原创: 前端研发团队 爱奇艺技术产品团队 昨天
- pip或easy_install安装库报错:SSL: CERTIFICATE_VERIFY_FAILED
使用pip和easy_install安装那个lxml.pyspider这些库或者框架一直提示以下错误: Collecting pyspider Could not fetch URL https:// ...
- contenttypes - django组件
一.contenttypes介绍 它的作用:可以通过两个字段让表和N张表创建FK关系 二.ContentType.GenericForeignKey.GenericRelation 表结构: from ...
- 创建list方法总结
版权声明:本文为博主原创文章,未经博主同意不得转载. https://blog.csdn.net/sheismylife/article/details/28878593 构建一个list 注意要标记 ...
- [py]pycharm远程环境添加
pycharm配置settings.jar pycharm远程环境调用.zip xadmin xadmin-django2 pycharm激活 最新2018.2激活---更新2018年8月8日 15: ...
- [svc]ftp协议数据连接的2种模式
玩明白了以太网2的二层数据格式, ip格式 tcp/udp个时候, 需要玩一玩一些有用的基于这些已上的协议数据了. 如 dhcp ftp等.比较有趣. ftp协议 分控制连接21端口 和数据连接 20 ...
- iis服务器配置
对应的步骤在文件中上传了rar文件 1 .net framework 4.0 和 framework 4.5 直接安装程序 先安装4.0 再安装4.5 顺序不能颠倒!下载完直接安装 如果有会提示本机 ...
- CSS选择器可以用数字开头吗
最好是字母开头,后面用数字可以,直接用数字开头不符合官方规范,虽然浏览器牛逼点也能解析出来,但是最初就不要这么做,坏习惯养成很难改.而且如果团队合作,css的命名都需要有固定的格式,还要有可读性方便他 ...
- sql server 中的分区函数用法(partition by 字段)
partition by关键字是分析性函数的一部分,它和聚合函数不同的地方在于它能返回一个分组中的多条记录,而聚合函数一般只有一条反映统计值的记录,partition by用于给结果集分组,如果没 ...