V-rep学习笔记：并联机构正逆运动学

　　Solving the FK problem of simple kinematic chains is trivial (just apply the desired joint values to all joints in the chain to obtain the position and orientation of the tip or end effector). However it is less trivial to solve the IK and FK problem for closed mechanisms. 计算串联机构（或开链机构）的运动学正解很简单，但是对于并联机构或者闭链机构（若运动链的各构件构成了首末封闭的系统，则称其为闭式运动链）来说运动学正解的计算就比较复杂。

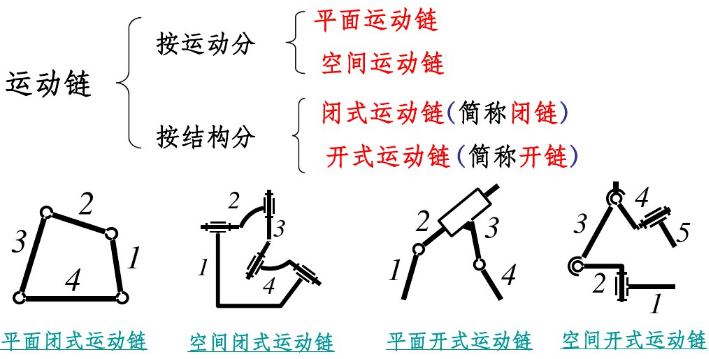
Solving IK and FK for closed mechanisms

　　In the case of an FK problem, identify the joints that you want to control (i.e. the joints that are driving the mechanism, the active joints—select the joint mode different from inverse kinematics mode). Then, identify which kinematic chain needs to be closed. Closing will be handled by loop closure constraints in the form of tip-target pairs as shown in following figure:

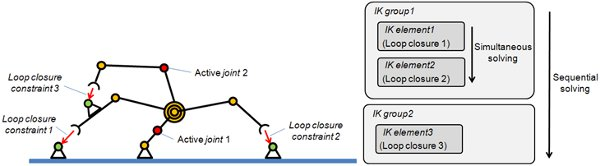
[Forward Kinematics solving method for closed mechanisms]

　　Then, set the desired joint values for the active joints and call the inverse kinematics functionality to handle loop closure constraints. (the default main script handles all IK groups that are not marked as explicit handling). Following example shows some additional functionality that can be used to solve complicated kinematic problems:

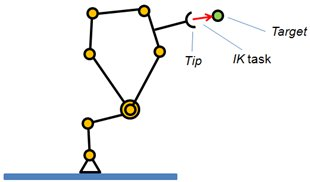
[Inverse kinematics task]

　　Most of the time there are several different ways of solving the IK or FK of a mechanism, and it is always worth considering various alternatives before implementing the most complicated one!

　　参考V-REP_PRO_EDU\scenes\ik_fk_simple_examples\7-fkAndIkResolutionForParallelMechanisms.ttt中的例子，实现了闭链机构的运动学正解与逆解：

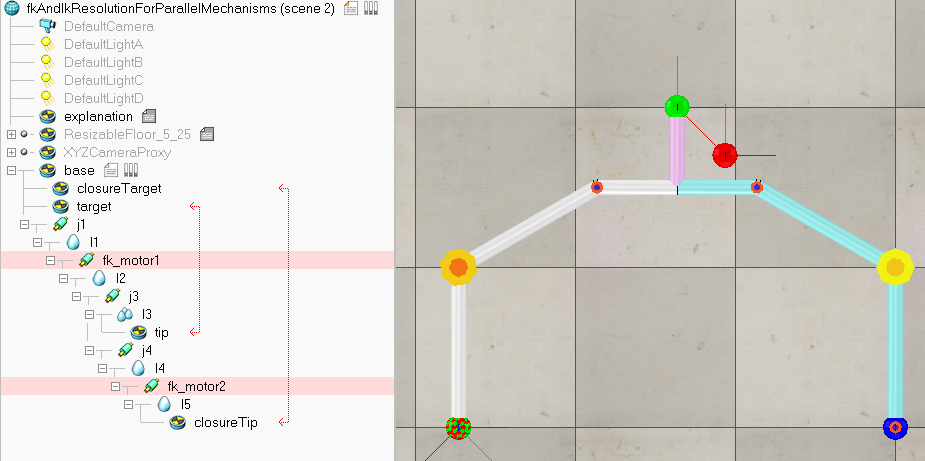
　　根据这个例子我们来搭建一个平行四边形机构。构建树形层级结构：以frame作为机座，然后将运动链上的节点依次串联起来，最后将target和tip连接起来构成闭环（loop closure）。target和tip的类型设置为IK,tip-target，然后在Calculation Modules的IK选项卡中添加IK group，并将其设为显式处理（Explicit handling）：

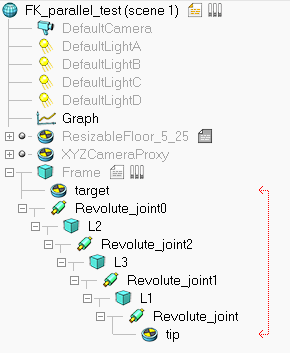[模型结构]

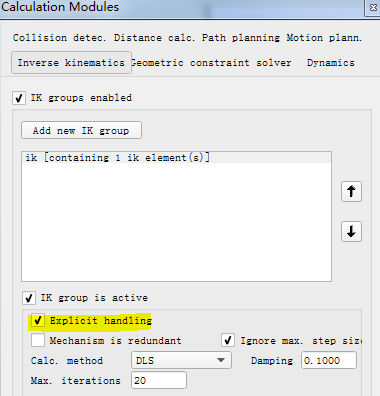
[IK设置]

　　给第一个关节（主动控制关节。其它关节从动但要设为IK模式，而不是passive模式）施加一个正弦规律的往复摆动，可以看出机构能跟着一起运动而不散开。添加Graph记录末端关节转角和运动链上倒数第二个关节的转角，可以看出末端关节转角为0且始终保持不变（其实这里末端的Joint并没有什么作用，因为在IK的计算下tip和target已经能重合。比如上面官方的那个例子中最后一根杆L5就没有接Joint而是直接连着tip）。

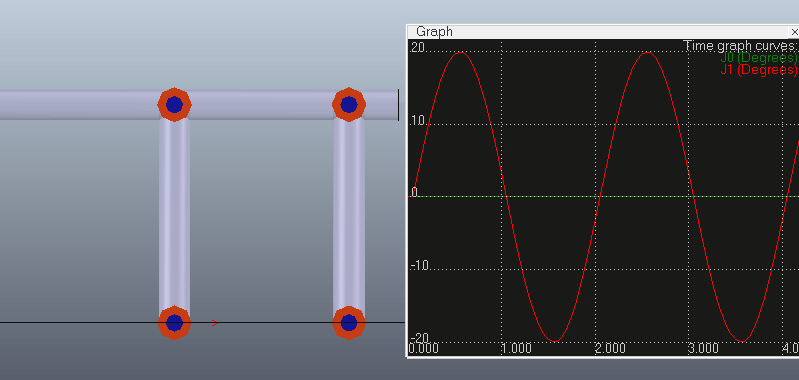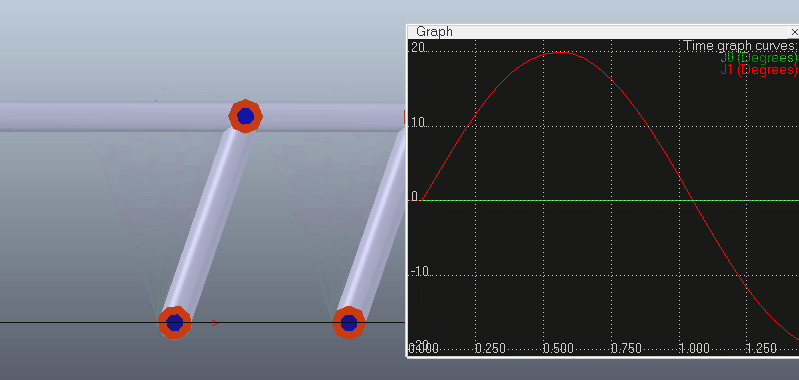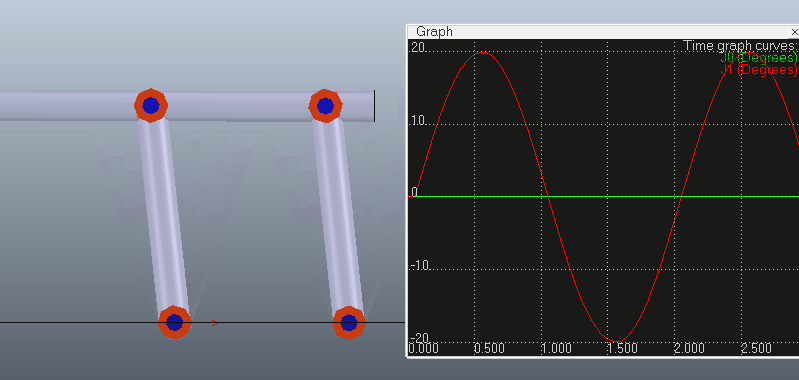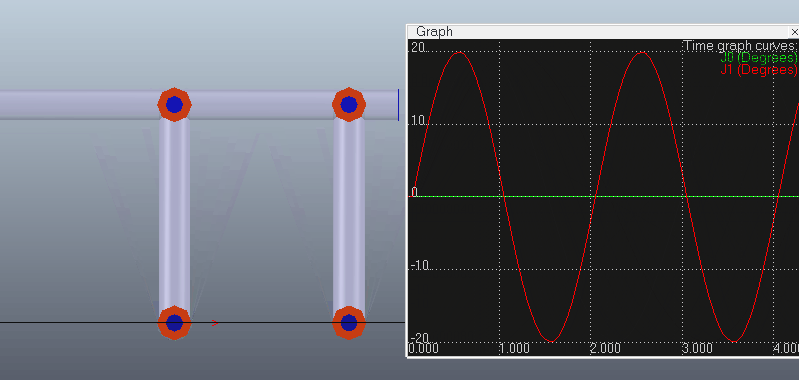
　　代码如下，在设置主动关节角度后可以调用simHandleIkGroup函数来计算IK，使机构保持闭环：

if (sim_call_type==sim_childscriptcall_initialization) then

    ikGroup=simGetIkGroupHandle('ik')
    tipDummy=simGetObjectHandle('tip')
    motor=simGetObjectHandle('Revolute_joint0')

    -- set the motor joint into ik mode
    simSetJointMode(motor,sim_jointmode_ik,)

    -- close the mechanism (if it was open)
    simHandleIkGroup(ikGroup)
end

if (sim_call_type==sim_childscriptcall_actuation) then

    -- First set the motor joint into passive mode
    simSetJointMode(motor,sim_jointmode_passive,)

    -- Set the desired joint angle
    local angle=*math.pi/*math.sin(math.pi*simGetSimulationTime())
    simSetJointPosition(motor, angle)

    -- Compute
    simHandleIkGroup(ikGroup)
end

　　

　　注意使用几何约束求解器GCS也能实现类似的功能，只是相比IK存在着一些差异：The geometric constraint solver is slower and less precise at solving kinematic problems, but might be easier and more intuitive to use. Moreover, it allows interacting with a mechanism in a more flexible way than the inverse kinematics calculation module.

　　下面场景中可以拖拽机构上的任意杆件来直观地控制其运动。这里使用的是Geometric Constraint Solver（注意要设置好General damping参数，否则可能出现拖拽时机构不动、动的很迟缓或者约束broken的现象）

参考：

Solving IK and FK for any type of mechanism

V-rep学习笔记：机器人逆运动学解算

V-rep学习笔记：Geometric Constraint Solver（几何约束求解）