培训补坑（day10:双指针扫描+矩阵快速幂）

这是一个神奇的课题，其实我觉得用一个词来形容这个算法挺合适的：暴力。

是啊，就是循环+暴力。没什么难的。。。

先来看一道裸题。

那么对于这道题，显然我们的暴力算法就是枚举区间的左右端点，然后通过前缀和统计结果。时间复杂度O(n^2)，但是如果我们的数据范围到了100000，那么我们的算法就T了。

于是我们考虑一个性质。如果我们发现一个区间，这个区间的sum<k，那么被这个区间包含的区间都不可能是答案。

所以我们用两个指针（左右端点。）如果目前区间的sum<k，我们就延伸右端点。否则我们就统计答案，然后让左端点往右移。直到2个指针都到达n，结束枚举。

这显然很水对吧。

那么我们来一道稍难的问题。

那么我们先想一下我们的策略，假如我们把所有的区间按照区间长度排序，那么我们的答案一定是其中的连续一段区间。因为跳着取肯定没有连着取更优。

那么我们接下来就是判断区间的覆盖次数了。显然我们可以用线段树轻松解决这个问题。

说起来挺简单，其实实现起来还是挺复杂的。

下面贴上代码

#include<cstdio>
#include<algorithm>
#define min(a,b) ((a)<(b)?(a):(b))
#define max(a,b) ((a)>(b)?(a):(b))
#define ls (k<<1)
#define rs (k<<1|1)
#define M 500005
#define MN 1<<20
#define inf 0x3f3f3f3f
using namespace std;
int n,m,cnt,l[M],r[M],rk[M],val[M<<],t[MN<<],ans=inf,mark[MN<<],len[M];
int find(int x){
    int le=,re=cnt;
    while(le<re){
        int mid=le+re>>;
        if(val[mid]<x)le=mid+;
        else re=mid;
    }return le;
}
void pushdown(int k){mark[ls]+=mark[k],mark[rs]+=mark[k],t[ls]+=mark[k],t[rs]+=mark[k],mark[k]=;}
void fpush(int k){t[k]=max(t[ls],t[rs]);}
void update(int l,int r,int a,int b,int k,int ad){
    if(a<=l&&r<=b){mark[k]+=ad;t[k]+=ad;return;}if(l!=r&&mark[k])pushdown(k);int mid=l+r>>;
    if(a<=mid)update(l,mid,a,b,ls,ad);
    if(b>mid)update(mid+,r,a,b,rs,ad);
    fpush(k);
}
bool cmp(int a,int b){return len[a]>len[b];}
int main(){
    scanf("%d%d",&n,&m);
    for(int i=;i<=n;i++)scanf("%d%d",&l[i],&r[i]),len[i]=r[i]-l[i],rk[i]=i,val[i<<]=l[i],val[i<<|]=r[i];
    sort(val+,val+(n<<)+);sort(rk+,rk+n+,cmp);
    for(int i=;i<=(n<<)+;i++)if(val[i-]!=val[i])val[++cnt]=val[i];
    for(int i=;i<=n;i++)l[i]=find(l[i]),r[i]=find(r[i]);
    for(int le=,re=;le<=n;le++)
        for(update(,cnt,l[rk[le]],r[rk[le]],,);t[]>=m;re++){
            update(,cnt,l[rk[re]],r[rk[re]],,-);
            ans=min(len[rk[re]]-len[rk[le]],ans);
        }
    printf("%d\n",ans==inf?-:ans);
} 

————————————————我是分割线————————————————

第一块讲完啦！接下来第二块。

矩阵快速幂=矩阵+快速幂。。

我记得我讲过。。但是博客不见了⌇●﹏●⌇吓死宝宝惹

无奈的重讲一遍。

首先我们要了解一下矩阵。。（虽然我们夏令营的时候讲过，但是显然向量内积什么的特别难理解，所以我们不要管理念）

总之就是n*m个数的集合。

然后我们理解一下矩阵乘法的定义

直接上图

那么我们用矩阵乘法解决什么问题呢？

答：dp问题。

是不是很奇怪？

但是其实并不难理解、

我们举个例子。

假设我们已知DP式子：dp[i]=dp[i-1]+dp[i-2]，假如我们想要直接得到dp的第n项，而且n的值特别大，比如10^18，那么显然我们不能On推过去。

那怎么办呢？我们可以把dp方程转移为一个矩阵。

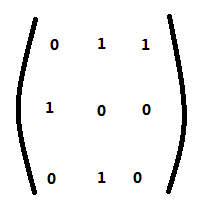
那么我们得到的这个矩阵表示，假如说我们把矩阵的第一位变为矩阵的第二位和矩阵的第三位之和，把矩阵的第二位变为矩阵的第一位，矩阵的第三位变为矩阵的第二位。

由于每次的转移方程都不变，所以我们只要把这个矩阵做快速幂就好了。

是不是很简单？

下面贴上例题&&代码

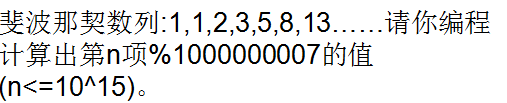
代码：

#include<cstdio>
#include<cstring>
using namespace std;
#define ll long long
#define MOD 1000000007
struct mat
{
    int z[][];
    mat(){memset(z,,sizeof(z));}
    mat operator*(mat b)
    {
        mat c;int i,j,k;
        for(i=;i<;++i)for(j=;j<;++j)
            for(k=;k<;++k)c.z[i][j]=(c.z[i][j]+(ll)z[i][k]*b.z[k][j])%MOD;
        return c;
    }
}f,x;
mat pow(ll x)
{
    mat r=f,t=f;
    for(--x;x;x>>=,t=t*t)if(x&)r=r*t;
    return r;
}
int main()
{
    ll n;
    f.z[][]=f.z[][]=f.z[][]=;
    x.z[][]=x.z[][]=;
    scanf("%lld",&n);
    printf("%d",(x*pow(n-)).z[][]);
}