[agc004f]Namori 贪心

Description

​ 现在给你一张NN个点MM条边的连通图，我们保证N−1≤M≤NN−1≤M≤N，且无重边和自环。

​ 每一个点都有一种颜色，非黑即白。初始时，所有点都是白色的。

​ 想通过执行若干次某种操作的方式，来将所有的点变成黑色。操作方式如下：

​ 选择一对颜色相同的****相邻的节点（存在边直接连接彼此），将它们的颜色反转。即若原来都是白色，则都变成黑色，反之亦然。

​ 现在想知道，他能否通过执行这种操作以达到目的。如果可以，他还希望步数尽可能的少。

Input

​ 第一行有两个正整数NN和MM（2≤N≤1052≤N≤105，N−1≤M≤NN−1≤M≤N）

接下来MM行，每行2个正整数aa和bb（1≤a,b≤N1≤a,b≤N），表示每条边连接的两个点。

Output

​ 如果存在操作方案能达到目的，请输出最少操作次数。

否则，请输出−1−1

Sample Input

Sample Input 1
6 5
1 2
1 3
1 4
2 5
2 6

Sample Input 2
3 2
1 2
2 3

Sample Input 3
4 4
1 2
2 3
3 4
4 1

Sample Input 4
6 6
1 2
2 3
3 1
1 4
1 5
1 6

Sample Output

Sample Output 1
5

Sample Output 2
-1

Sample Output 3
2

Sample Output 4
7

HINT

​ 如第一个样例中，存在如下操作方案：

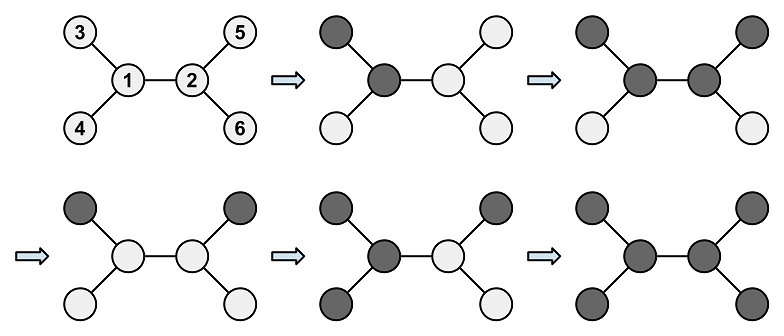
Sol

如果是一棵树，我们把深度为奇数的点赋值为1，偶数-1，然后判断总和是否为0即可。此时答案为\(\sum_{i=1}^{n}abs(s[i])\)，\(s[i]\)表示子树和。证明：我们让子树变成0的最小操作次数就是绝对值，因为一次操作至多改变1。

如果是个基环树，那么我们判断这个环连的两个点深度是否同奇同偶，同的话每次能够且仅能够添加或者删除2个权值，这样的话我们判断sum是不是一个偶数，是的话我们把s[u]和s[v]减去sum/2，然后做一次树的做法即可。

如果不同，说明我们无法改变总和，只能通过这个边进行直接对于不同深度的传输，我们假设u的权值+x，v的权值-x（只是系数，x能是任何数字），然后我们进行系数的子树和，这样的话求出系数为1或者-1的所有点，这些点是要加上x的，剩下的直接取abs，加上x的地方我们把它系数置为1（改变数字的正负强制改变系数），然后丢进一个数组，排序后取中位数即为最优解。

Code

#include <bits/stdc++.h>
using namespace std;
int fa[100005],c[100005],d[100005],s[100005],g[100005],i,j,k,l,t,n,m,u,v,a,b,x,tot,num,vis[100005],ok;
long long ans;vector<int>e[100005];
void dfs1(int x,int y)
{
	vis[x]=1;
	for(int i=0;i<e[x].size();i++) if(e[x][i]!=y)
	{
		if(vis[e[x][i]]){u=x;v=e[x][i];if(c[u]==c[v]) ok=1;}
		else{c[e[x][i]]=c[x]^1;dfs1(e[x][i],x);}
	}
}
void dfs(int x,int y)
{
	for(int i=0;i<e[x].size();i++) if(e[x][i]!=y&&!((x==u&&e[x][i]==v)||(x==v&&e[x][i]==u)))
		dfs(e[x][i],x),d[x]+=d[e[x][i]],s[x]+=s[e[x][i]];
}
int main()
{
	scanf("%d%d",&n,&m);
	for(int i=1;i<=m;i++) scanf("%d%d",&j,&k),e[j].push_back(k),e[k].push_back(j);
	c[1]=1;dfs1(1,0);
	for(int i=1;i<=n;i++) s[i]=c[i]?1:-1;
	for(int i=1;i<=n;i++) num+=s[i];
	if(m==n-1){if(num){printf("-1\n");return 0;}}
	else
	{
		if(ok){if(abs(num%2)==1){printf("-1\n");return 0;}s[u]-=num/2;s[v]-=num/2;ans+=(long long)abs(num/2);}
		else{if(num){printf("-1\n");return 0;}d[u]=1;d[v]=-1;}
	}
	dfs(1,0);
	for(int i=1;i<=n;i++) if(!d[i]) ans+=(long long)abs(s[i]);else g[++tot]=-s[i];
	g[++tot]=0;sort(g+1,g+tot+1);x=g[(tot+1)/2];
	for(int i=1;i<=tot;i++) ans+=(long long)abs(g[i]-x);
	printf("%lld\n",ans);
}