拥挤的奶牛题解---队列优化DP---DD(XYX)​​​​​​​的博客

拥挤的奶牛

时间限制: 1 Sec  内存限制: 128 MB

题目描述

FJ的n头奶牛（1<=n<=50000）在被放养在一维的牧场。第i头奶牛站在位置x(i)，并且x(i)处有一个高度值h(i)

（1<=x(i),h(i)<=1000000000）。

一头奶牛感觉到拥挤当且仅当它的左右两端都有一头奶牛所在的高度至少是它的2倍，且和它的距离最多为D。尽管感到拥挤的奶牛会产生更少的牛奶，FJ还是想知道一共有多上感到拥挤的奶牛。请你帮助他。

输入

第一行：两个整数n和D。

第二行到第n+1行：每一行有两个数表示x(i)和h(i)。

输出

一个数k表示感到拥挤的奶牛的数量。

方法

这道题确实烧脑，因为它没办法用单调队列去存。 假设 i 大于队末元素 j ，则在普通的下降单调队列中， j 就因该被计算并且出队，但是若 i 并不大于等于 2 * j ，就不能计算 j 。若此时把 i 直接入队，就缺乏单调性，不方便计算了。

既然此题数据过大，需要优化，却又不能用单调队列/栈的话，能不能只利用它 O(2n) 的优点，采用更灵活的结构呢？

我的想法是，先按照位置排序，然后用一个优先队列，令 (node)a < b 为 a.h < b.h，用小根堆优化。跟单调队列差不多。每次有元素 x 入堆，就先把堆顶(最矮的那些)身高不超过 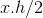 的奶牛计算了，如果有与 x 的距离超过 D 的，就直接出堆，然后再把 x 入堆。计算两遍，一次计算右边有无拥挤，一次计算左边。

这样一来，每个元素仍然只有 入堆，出堆 两种计算，时间复杂度也还是 n 的常数倍！

#include<cstdio>
#include<iostream>
#include<algorithm>
#include<queue>
#include<vector>
using namespace std;
void read(int &x) {
    int f = 1;x = 0;char s = getchar();
    while(s < '0' || s > '9') {if(s == '-')f = -1;s = getchar();}
    while(s >= '0' && s <= '9') {x = x * 10 + s - '0';s = getchar();}
    x *= f;
}
struct no{
    int id,x,h;
}a[50005];
bool operator < (no a,no b) {
    return a.h < b.h;
}
bool operator > (no a,no b) {
    return b < a;
}
int n,m,s,o,i,j,k;
bool l[50005],r[50005];
priority_queue<no,vector<no>,greater<no> > b;
bool cmp(no a,no b) {
    return a.x < b.x;
}
int main() {
    read(n);read(m);
    for(i = 1;i <= n;i ++) {
        read(a[i].x);read(a[i].h);
        a[i].id = i;
    }
    sort(a + 1,a + 1 + n,cmp);
    b.push(a[1]);
    for(i = 2;i <= n;i ++) {
        while(!b.empty() && a[i].h >= b.top().h * 2) {
            if(a[i].x - b.top().x <= m) {
                r[b.top().id] = 1;
            }
            b.pop();
        }
        b.push(a[i]);
    }
    while(!b.empty()) b.pop();
    b.push(a[n]);
    for(i = n - 1;i > 0;i --) {
        while(!b.empty() && a[i].h >= b.top().h * 2) {
            if(b.top().x - a[i].x <= m) {
                l[b.top().id] = 1;
            }
            b.pop();
        }
        b.push(a[i]);
    }
    for(i = 1;i <= n;i ++) {
        if(l[i] && r[i]) k ++;
    }
    printf("%d",k);
    return 0;
}