遗传算法求TSP问题

一、实验内容及目的

本实验以遗传算法为研究对象，分析了遗传算法的选择、交叉、变异过程，采用遗传算法设计并实现了商旅问题求解，解决了商旅问题求解最合适的路径，达到用遗传算法迭代求解的目的。选择、交叉、变异各实现了两种，如交叉有顺序交叉和部分交叉。

二、实验环境

Windows10

开发环境Python 3/Flask

三、实验设计与实现

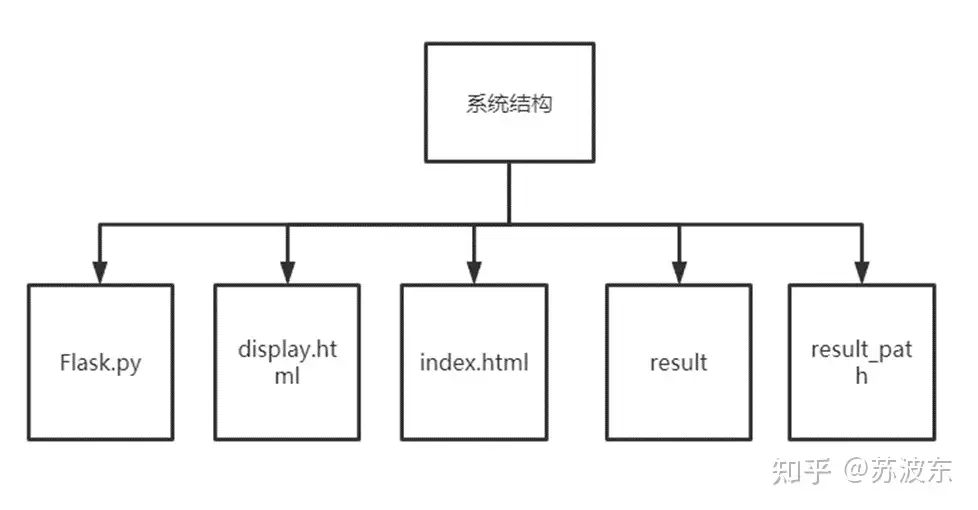
图1软件结构图

图1软件结构图

Flask.py是后端核心代码，里面是遗传算法实现，index.html为首页，即第一次进入网页的页面，进入之后可以进行参数设置，之后点击开始，参数会传到Flask.py中进行解析和算法运行，最终将迭代结果存到result（存储迭代结果图）和result_path（存储最短路径图）在返回给display.html页面显示。

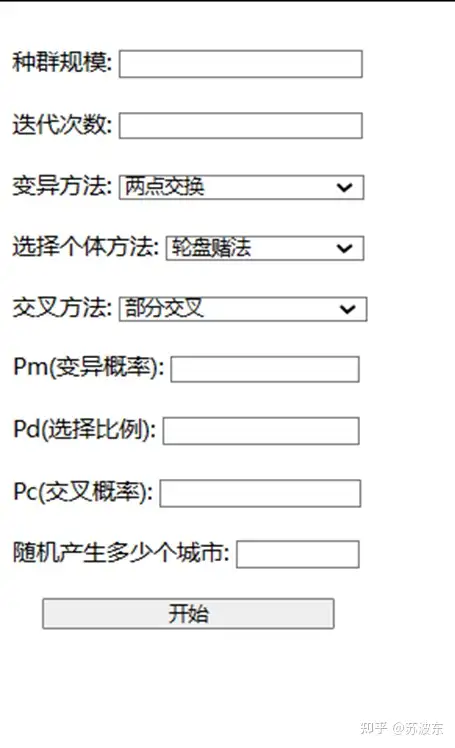
图2系统界面图

图2系统界面图

输入种群规模、迭代次数、变异概率、选择比例、交叉概率并选择变异方法、选择个体方法、交叉方法。点击开始即可运行该系统。

具体算法流程图：

图3核心算法流程图

流程图描述：首先根据参数城市数量和种群规模初始一个城市坐标矩阵的列表并计算城市间的距离存到矩阵，最后生成一个路径矩阵，这样就可以进入下一步计算适应度，每一条路径都有其路径距离值和适应度，接下来一次进行选择，交叉，变异操作，循环往复，直至达到了参数中的迭代次数限制。

选择—轮盘赌：（这里我的算法选出的种群数量不一定就恰好是根据比例算出的数量）

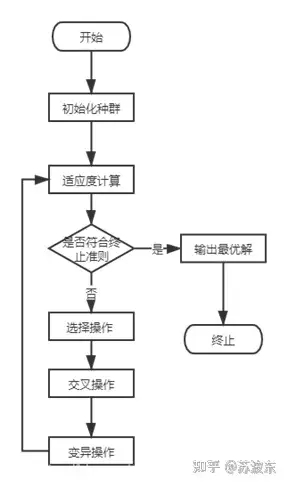
图3核心算法流程图

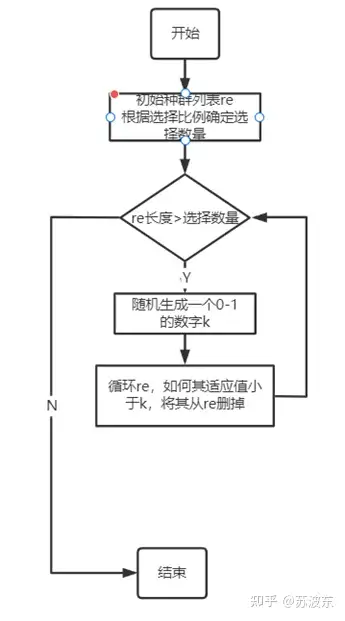
图4轮盘赌流程图

选择—锦标赛：

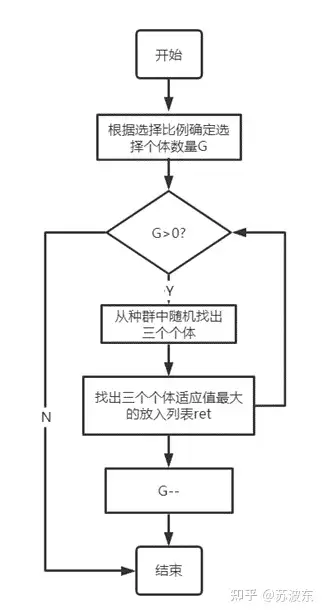
图5三元锦标赛流程图

交叉—顺序交叉：

1、 选切点X，Y

2、 交换中间部分

3、 从第二个切点Y后第一个基因起列出原顺序，去掉已有基因

4、 从第二个切点Y后第一个位置起，将获得的无重复顺序填入

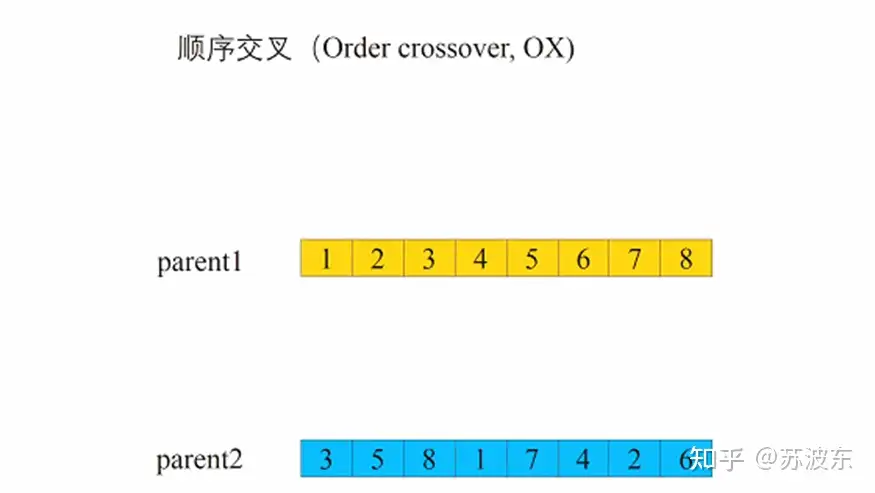
图6顺序交叉动态图

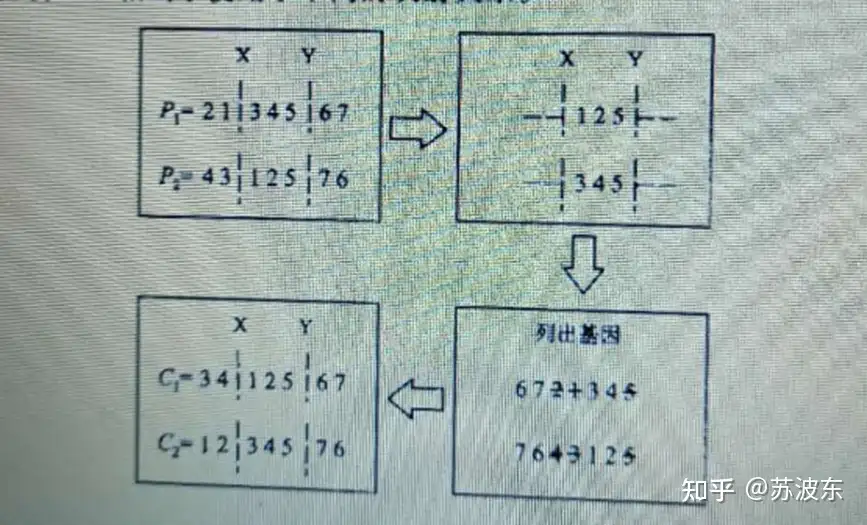
图7顺序交叉静态图

交叉—部分交叉：

1、 选切点oop

2、 选取oop到oop+3部分交换(我这里就是三个，你可以做成随机的几个）

3、 判断是否有重复的，若重复则进行映射，保证形成的新一对子代基因无冲突。

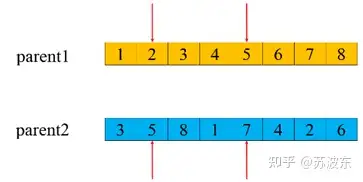
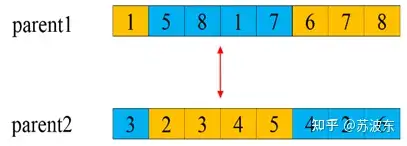
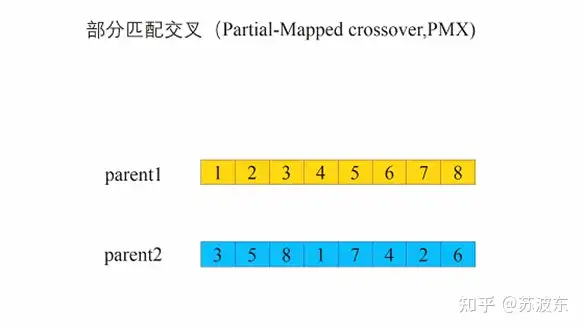
图8部分交叉动态图

变异—两点交换

1、 随机选取两点

2、 两点进行交换

变异—相邻交换

1、 随机选取一点

2、 和该点的后面点进行交换

适应度函数：经过测试得A取5，B取0效果好，所以实验中直接取了A=5,B=0运行

借鉴了sigmoid函数的形式，并对数据做了最大最小标准化，A、B是人为给定的常系数mean、max、min是种群所有个体的目标函数值的均值、最大值、最小值图像如下A=5,B=0

适应值较大的更容易进入下一代种群中

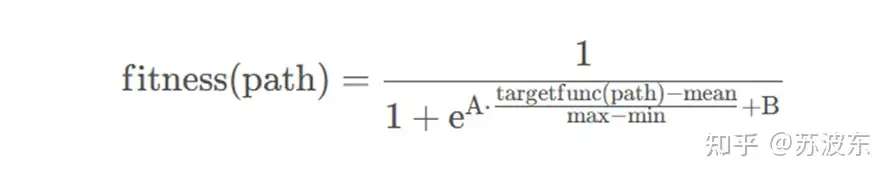
图9适应度函数算术表达式

四、实验结果与测试

表1 遗传算法解决TSP问题的测试用例

测试内容	测试用例	预期结果	实际结果
种群规模	1.不输入 2.输入除数字其他 3.输入整数数字 4.输入小数或者负数	失败 失败 成功 失败	与预期相同
迭代次数	5.不输入 6.输入除数字其他 7.输入整数数字 8.输入小数或者负数	失败 失败 成功 失败	与预期相同
变异方法	9.选择两点交换 10.选择相邻交换	成功 成功	与预期相同
选择个体方法	11.选择轮盘赌 12.选择锦标赛	成功 成功	与预期相同
交叉方法	13.选择部分交叉 14.选择顺序交叉	成功 成功	与预期相同
变异概率	15.不输入 16.输入除数字其他 17.输入小于1的小数 18.输入非小于1的小数或者整数	失败 失败 成功 失败	与预期相同
选择比例	19.不输入 20.输入除数字其他 21.输入小于1的小数 22.输入非小于1的小数或者整数	失败 失败 成功 失败	与预期相同
交叉概率	23.不输入 24.输入除数字其他 25.输入小于1的小数 26.输入非小于1的小数或者整数	失败 失败 成功 失败	与预期相同
随机产生多少个城市	27.不输入 28.输入除数字其他 29.输入整数数字 30. 输入小数或者负数	失败 失败 成功 失败	与预期相同

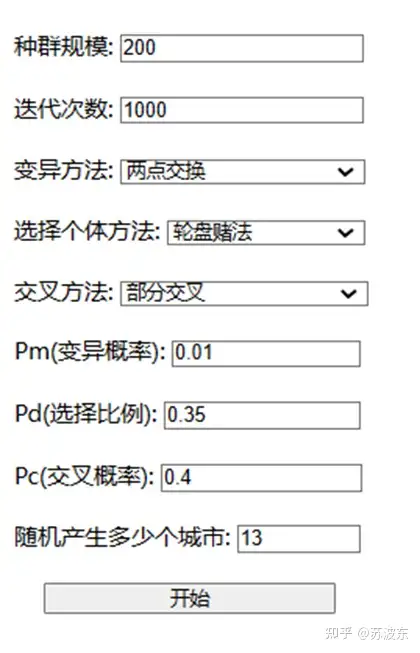
图10参数设置图

在上述参数设置好之后，即可开始运行系统，最后产生如图11的迭代结果图，最上面是自己的参数设置和最后生成的最小路径min_dist，图示整体为每次迭代的路径距离，可见随着迭代次数增加，路径距离一直减小最后趋于稳定。图12为用python画的路径图，图中横轴纵轴为城市位置的X,Y坐标。

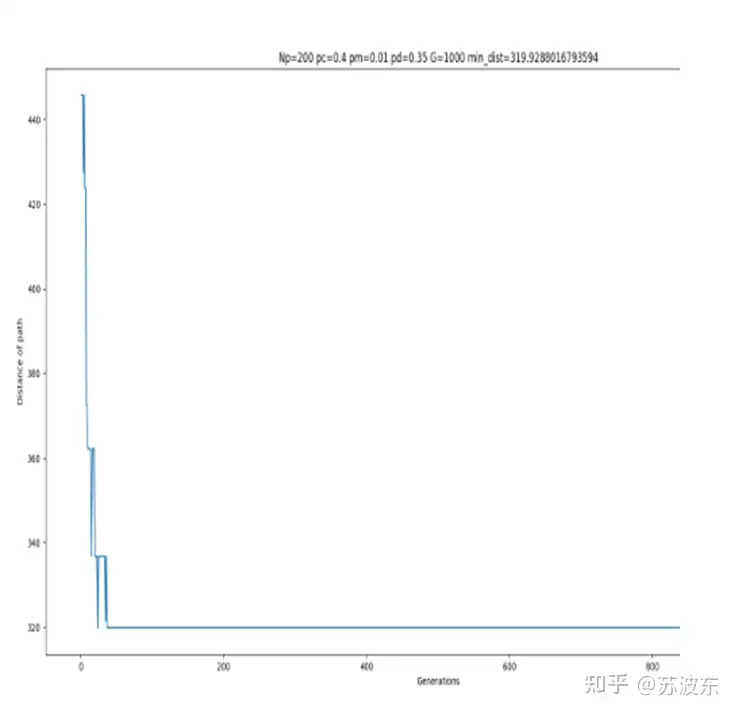
图11 迭代结果图

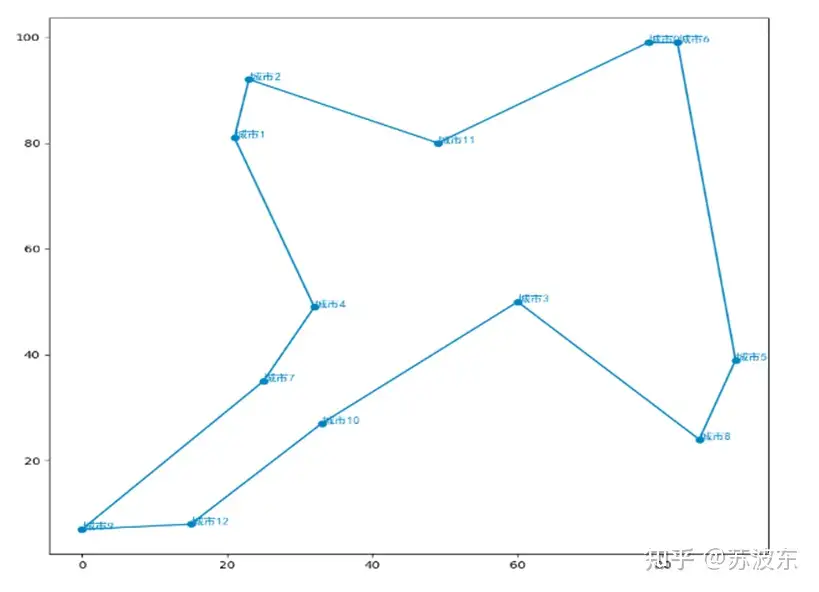
图12最短路径图

接下来重新选择其他参数来运行一下，看一下有没有区别。

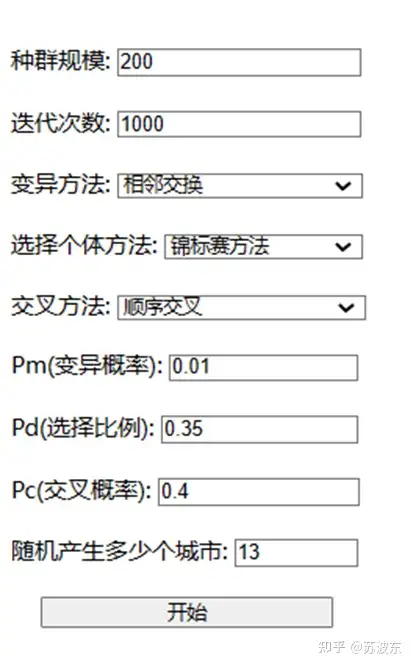
图13参数设置图

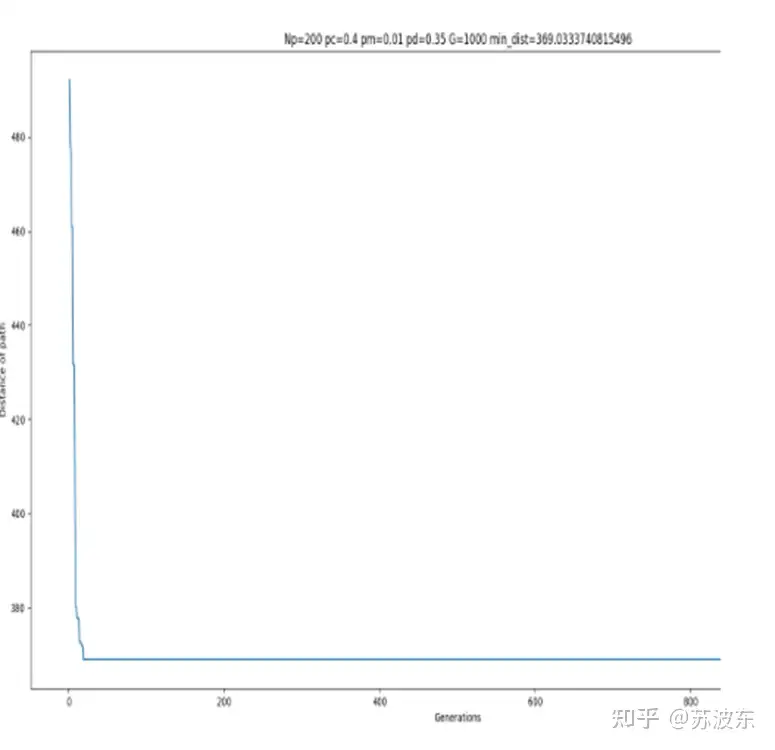
图14迭代结果图

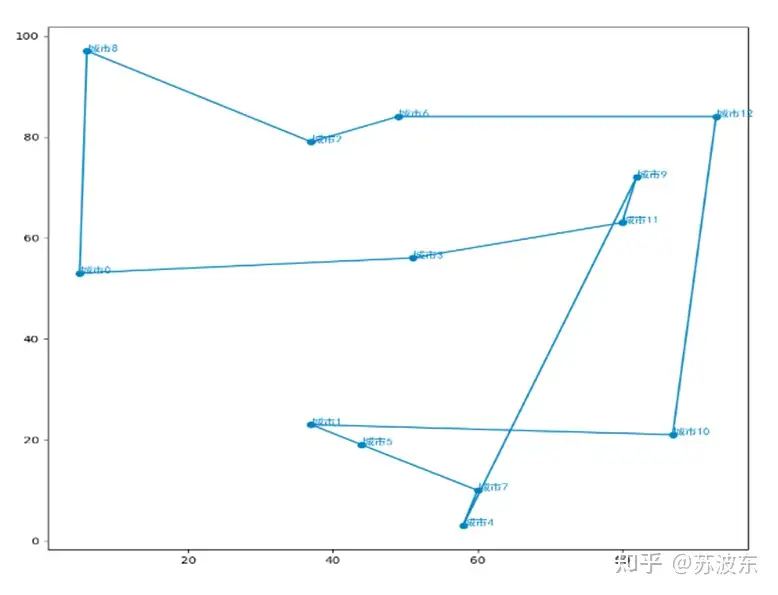
图15最短路径图

可以从迭代图像看出，参数不同会导致迭代中结果的不同，第一次参数设置的迭代中在前段迭代不稳定，忽上忽下，之后稳定，而第二次参数设置后迭代很快就稳定，没有忽上忽下的现象，所以不同的选择、变异、交叉方法会使迭代结果不同。所以可以根据随机设定让计算机找到最合适的参数设置。

欢迎关注我的知乎平台，我将持续为您解答一系列问题！