有向图的拓扑排序——DFS

在有向图的拓扑排序——BFS这篇文章中，介绍了有向图的拓扑排序的定义以及使用广度优先搜索（BFS）对有向图进行拓扑排序的方法，这里再介绍另一种方法：深度优先搜索（DFS）。

算法

考虑下面这张图：

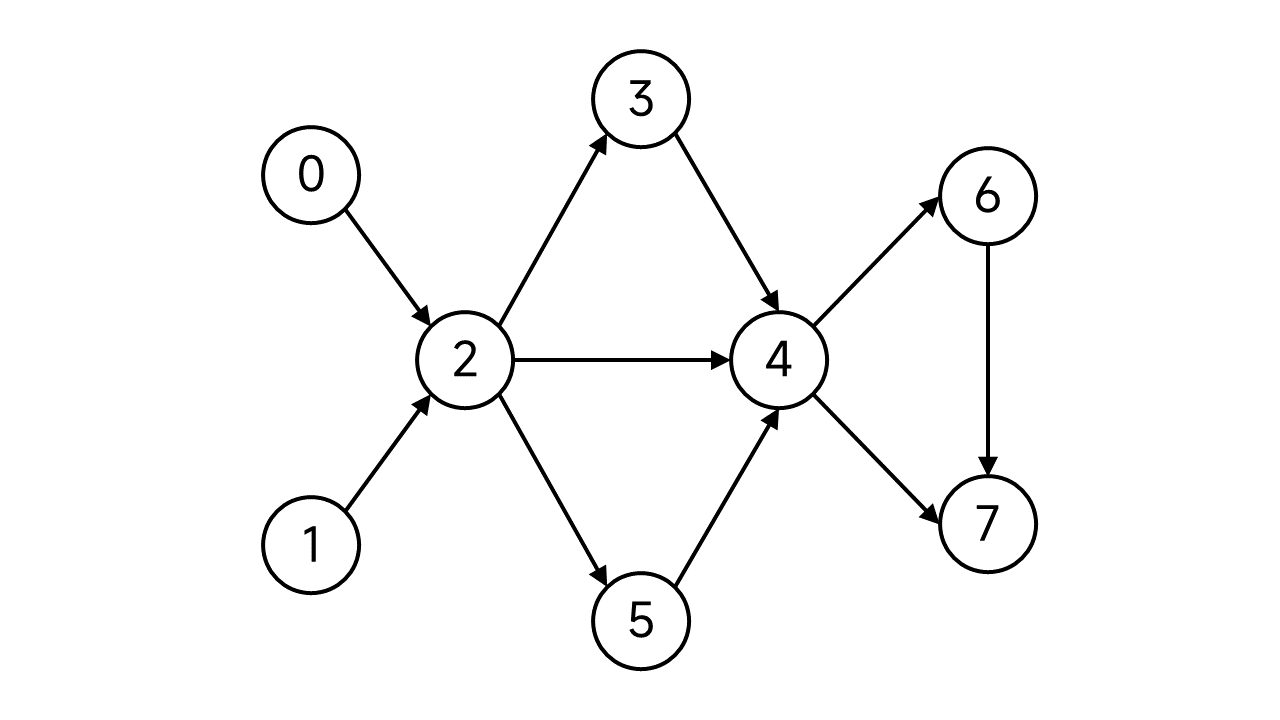
首先，我们需要维护一个栈，用来存放DFS到的节点。另外规定每个节点有两个状态：未访问（这里用蓝绿色表示）、已访问（这里用黑色表示）。

任选一个节点开始DFS，比如这里就从0开始吧。

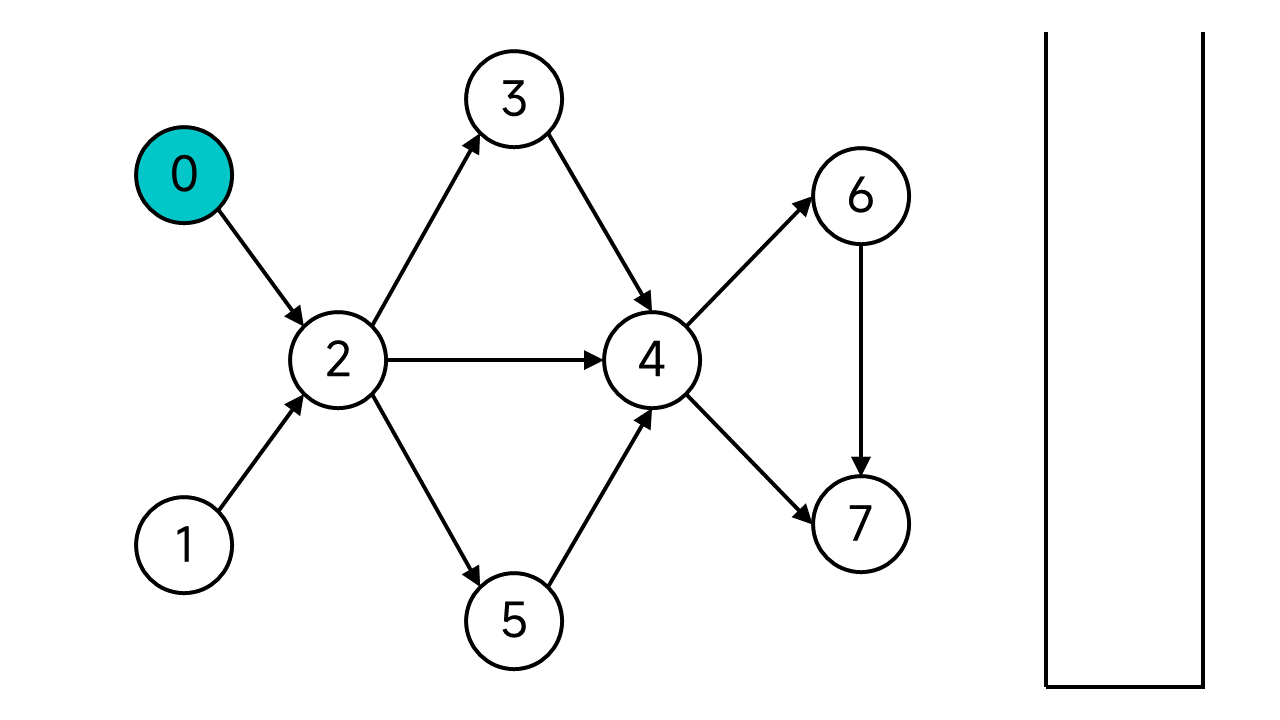
首先将节点0的状态设为已访问，然后节点0的邻居（节点0的出边指向的节点）共有1个：节点2，它是未访问状态，于是顺下去访问节点2。

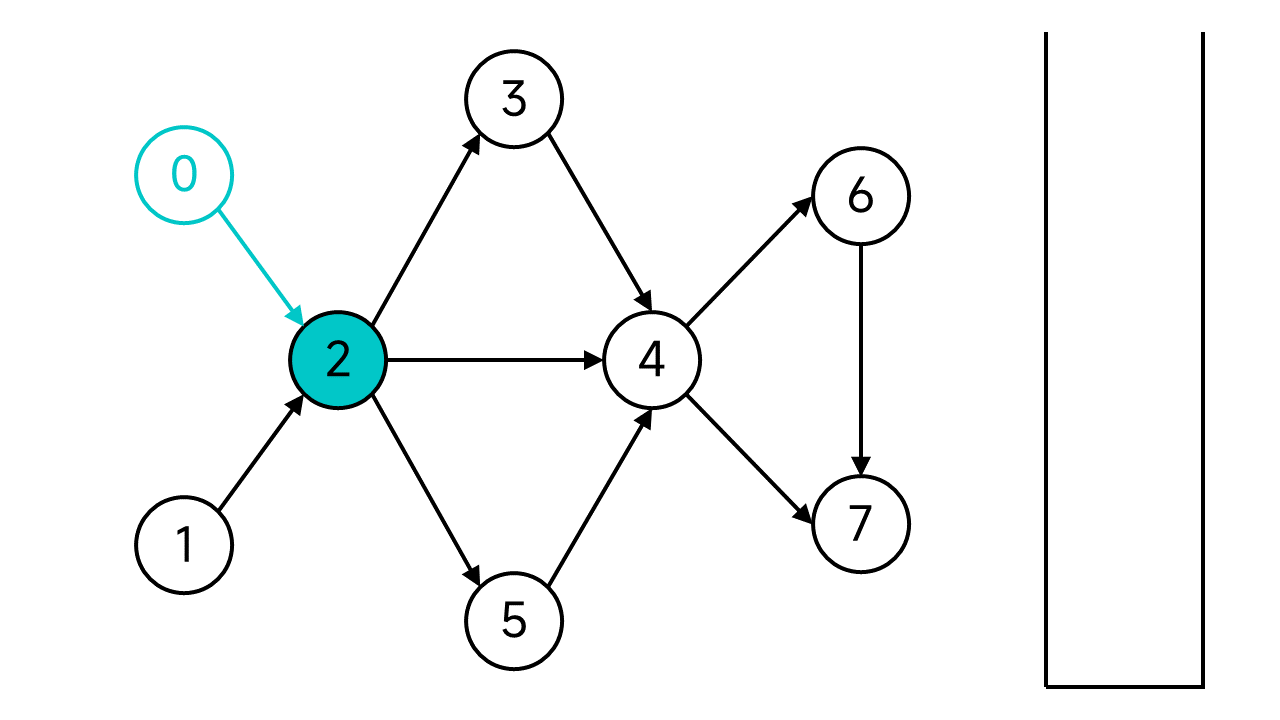
节点2的状态也设为已访问。节点2有3个邻居：3、4、5，都是未访问状态，不妨从3开始。一直这样访问下去，直到访问到没有出边的节点7。

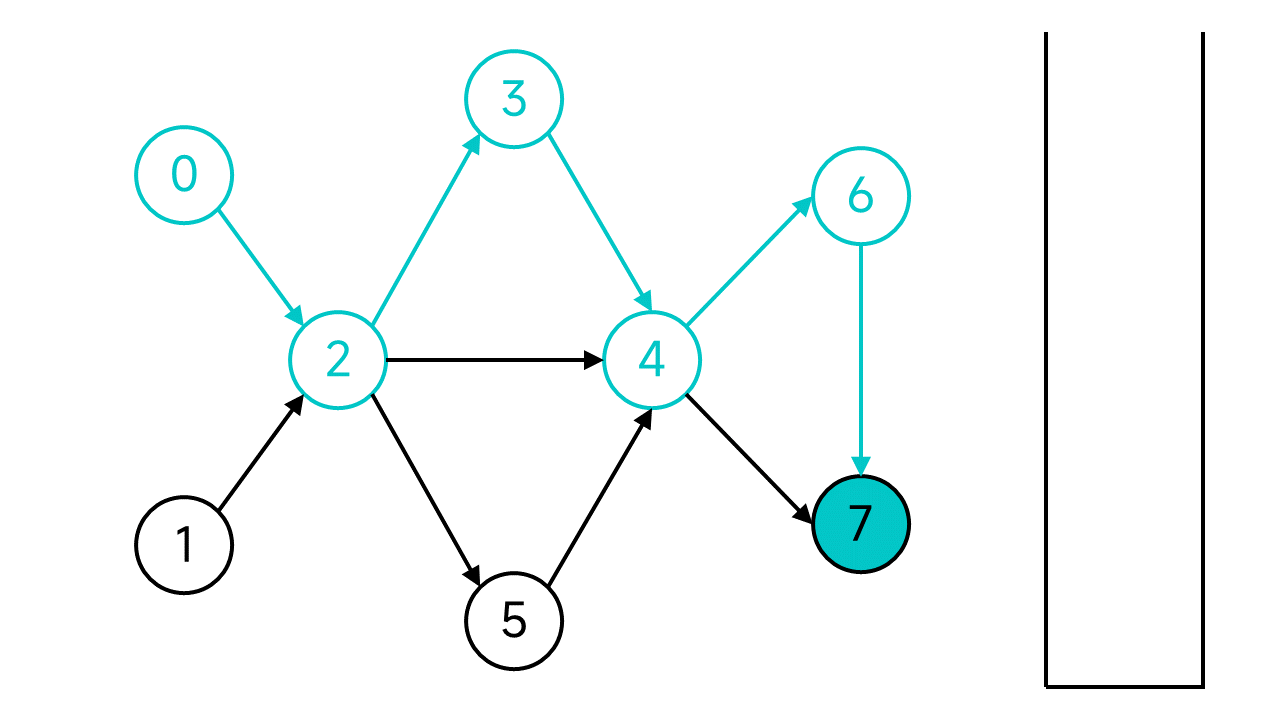
节点7没有出边了，这时候就将节点7入栈。

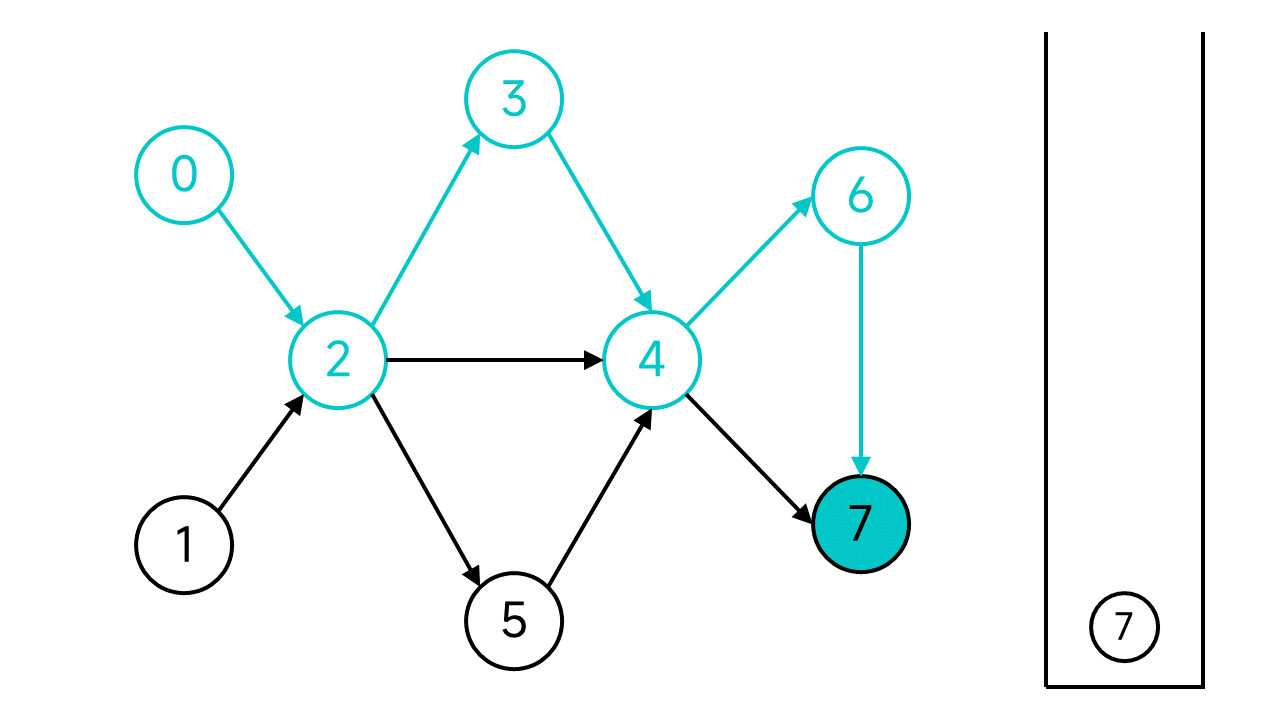
退回到节点6，虽然6还有邻居，但是唯一的邻居节点7是已访问状态，也入栈。再次退回，节点4的两个邻居也都已访问，依旧入栈并后退。以此类推，退回到节点2。

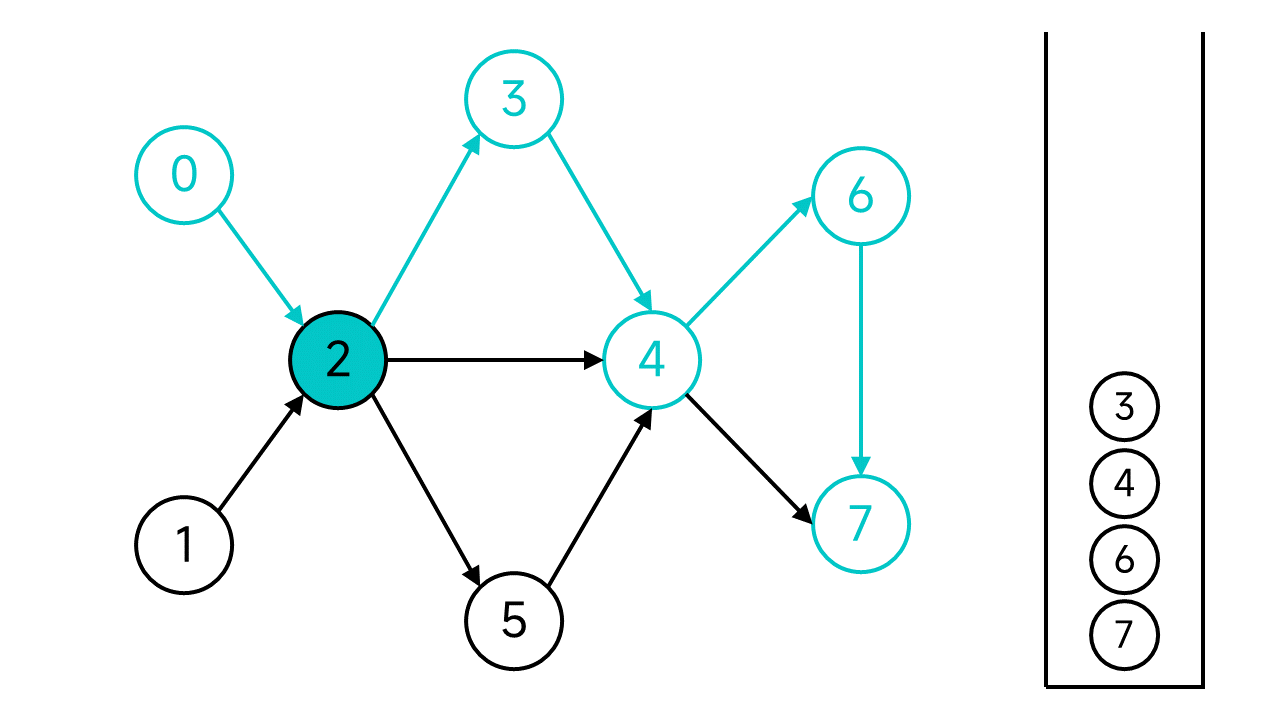
节点2有3个邻居，其中节点3和4已访问，但是节点5还未访问，访问节点5。

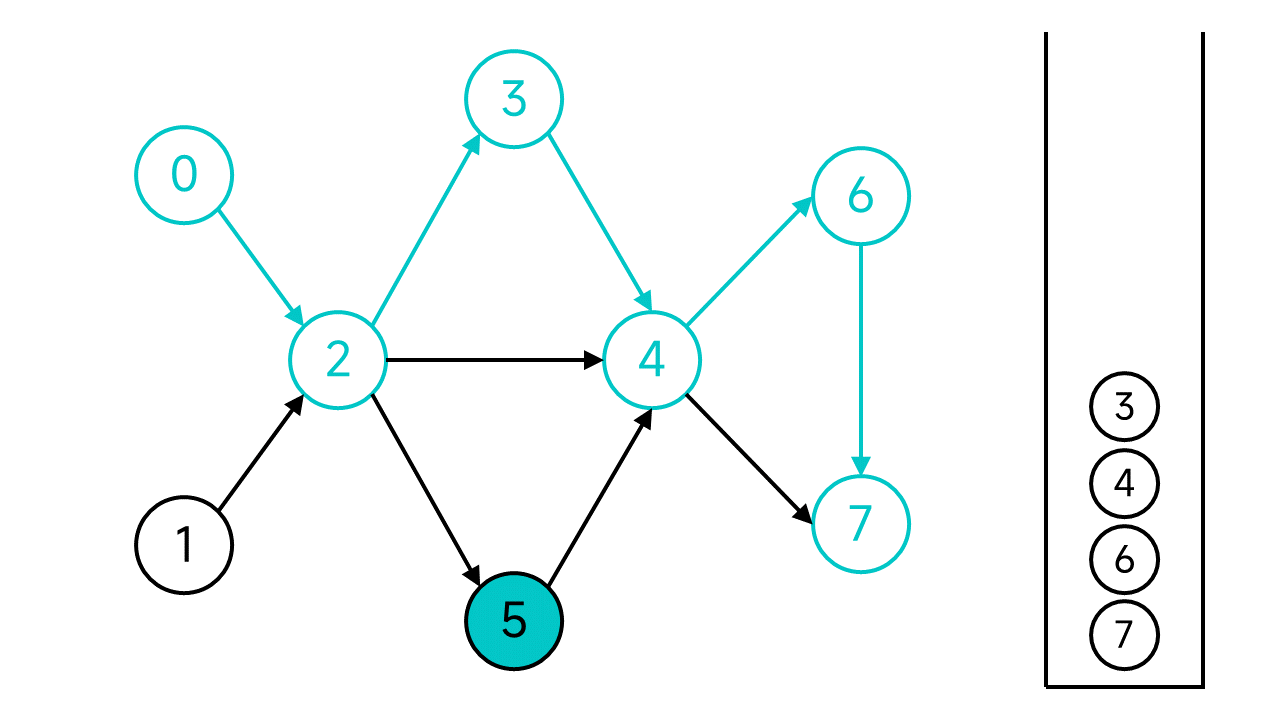
接下来的步骤是一样的，不再赘述了，直接退回到节点0并将0入栈。

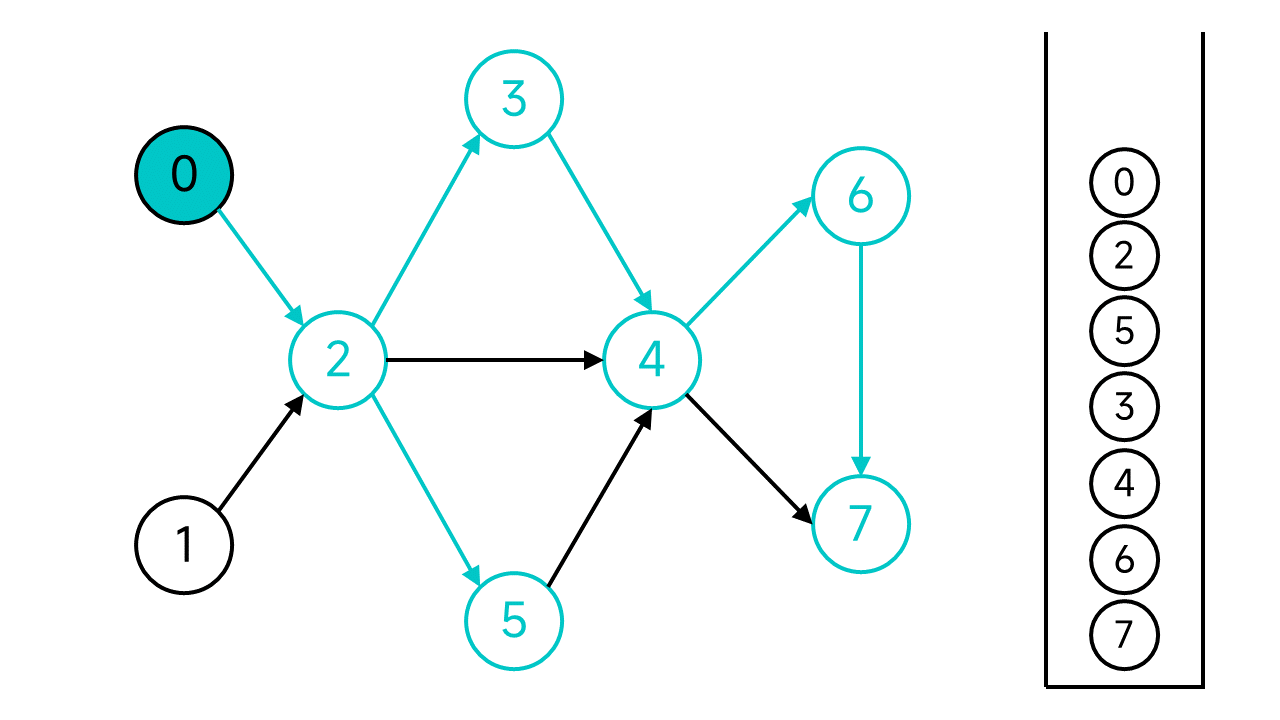
现在，从节点0开始的DFS宣告结束，但是图中还有未访问的节点：节点1，从节点1继续开始DFS。

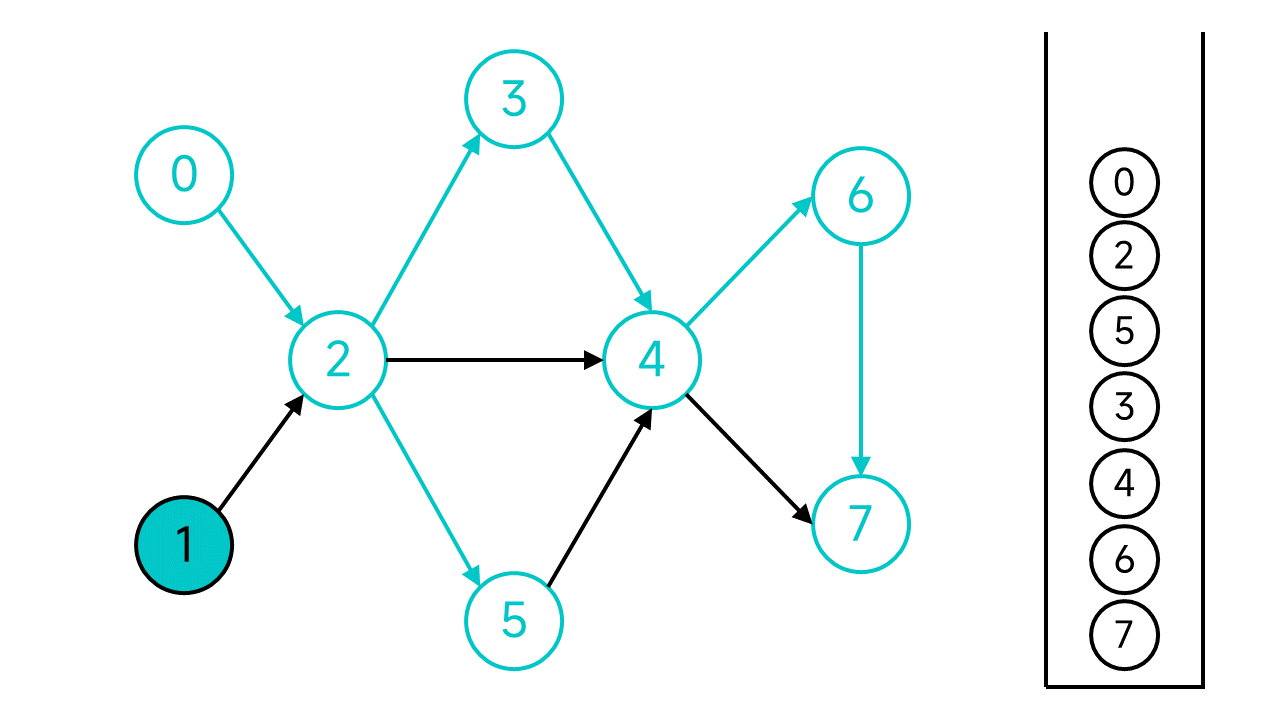
节点1的邻居节点2已经访问过了，直接将节点1入栈。

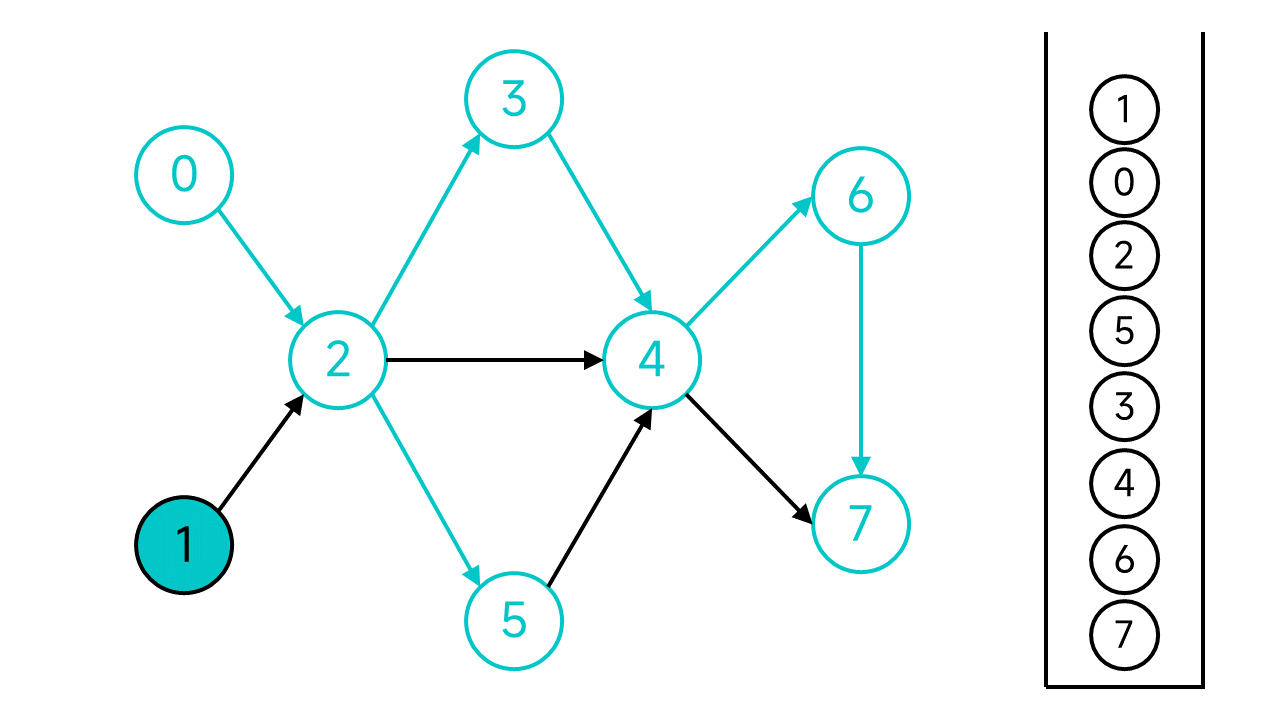
至此，整个DFS过程宣告结束。从栈顶到栈底的节点序列1 0 2 5 3 4 6 7就是整个图的一个拓扑排序序列。

实现

这里同样使用类型别名node_t代表节点序号unsigned long long：

using node_t = unsigned long long;

同样使用邻接表来存储图结构，整个图的定义如下：

class Graph {
    unsigned long long n;
    vector<vector<node_t>> adj;

protected:
    void dfs(node_t cur, vector<bool> &visited, stack<node_t> &nodeStack);

public:
    Graph(initializer_list<initializer_list<node_t>> list) : n(list.size()), adj({}) {
        for (auto &l : list) {
            adj.emplace_back(l);
        }
    }

    vector<node_t> toposortDfs();
};

DFS

函数dfs的参数及说明如下：

• cur：当前访问的节点。
• visited：存放各个节点状态的数组，false表示未访问，true表示已访问。初始化为全为false。
• nodeStack：存放节点的栈。

整个过程如下：

1. 首先，我们需要将当前节点的状态设为已访问：

visited[cur] = true;

1. 依次检查当前节点的所有邻居的状态：

for (node_t neighbor: adj[cur]) {
    // ...
}

1. 如果某个节点已访问，则跳过。

if (visited[neighbor]) continue;

1. 否则，递归的对该节点进行DFS：

dfs(neighbor, visited, nodeStack);

1. 所有邻居检查完后，就将该节点入栈：

nodeStack.push(cur);

整个dfs函数的代码如下：

void Graph::dfs(node_t cur, vector<bool> &visited, stack<node_t> &nodeStack) {
    visited[cur] = true;
    for (node_t neighbor: adj[cur]) {
        if (visited[neighbor]) continue;
        dfs(neighbor, visited, nodeStack);
    }
    nodeStack.push(cur);
}

拓扑排序

我们需要初始化3个数据结构：

• sort：存放拓扑排序序列的数组。
• visited：见上文。
• nodeStack：见上文。

vector<node_t> sort;
vector<bool> visited(n, false);
stack<node_t> nodeStack;

整个过程如下：

1. 依次检查每个节点的状态，如果未访问，则从该节点开始进行DFS：

for (node_t node = 0; node < n; ++node) {
    if (visited[node]) continue;
    dfs(node, visited, nodeStack);
}

1. 此时nodeStack已经存储了整个拓扑排序序列，我们只需要转移到sort数组并返回即可：

while (!nodeStack.empty()) {
    sort.push_back(nodeStack.top());
    nodeStack.pop();
}
return sort;

整个代码如下：

vector<node_t> Graph::toposortDfs() {
    vector<node_t> sort;
    vector<bool> visited(n, false);
    stack<node_t> nodeStack;
    for (node_t node = 0; node < n; ++node) {
        if (visited[node]) continue;
        dfs(node, visited, nodeStack);
    }
    while (!nodeStack.empty()) {
        sort.push_back(nodeStack.top());
        nodeStack.pop();
    }
    return sort;
}

测试

代码：

int main() {
    Graph graph{{2},
                {2},
                {3, 4, 5},
                {4},
                {6, 7},
                {4},
                {7},
                {}};
    auto sort = graph.toposortDfs();
    cout << "The topology sort sequence is:\n";
    for (const auto &node: sort) {
        cout << node << ' ';
    }
    return 0;
}

输出：

The topology sort sequence is:
1 0 2 5 3 4 6 7

复杂度分析

• 时间复杂度：\(O(n+e)\)，\(n\)为节点总数，\(e\)为边的总数。其中DFS的时间复杂度为\(O(n+e)\)。
• 空间复杂度：\(O(n)\)（邻接表的空间复杂度为\(O(n+e)\)，不计入在内），其中维护visited数组和nodeStack栈分别需要\(O(n)\)的额外空间。