UOJ244 【UER #7】短路

本文版权归ljh2000和博客园共有，欢迎转载，但须保留此声明，并给出原文链接，谢谢合作。

本文作者：ljh2000
作者博客：http://www.cnblogs.com/ljh2000-jump/
转载请注明出处，侵权必究，保留最终解释权！

Description

“第七套广播体操，原地踏步——走！”

众所周知，跳蚤们最喜欢每天早起做早操，经常天还没亮就齐刷刷地站在操场做着反复纵跳热热身。跳晚国在研制三星 note7 的时候注意到了这点，于是他们打算让炸弹更快地引爆，这样就可以消灭更多早起的跳蚤。

三星 note7 的主板可以看作是由(2n+1)×(2n+1) 个中继器构成的，某些中继器会有导线连在一起，左上角和右下角的中继器分别连着电源的正负极。

电流流过一根导线的时间可忽略不计，但当电流经过中继器时，会延缓一段时间再从中继器流出。这个时间只跟该中继器本身有关，我们把这段时间的长度称为中继器的延时值。

这些中继器由导线连接围成一个一个的层，同个层的中继器的种类都一样，而不同层的种类都不一样，可以发现总共有n+1 层。当n=4 时，主板大概长这样：

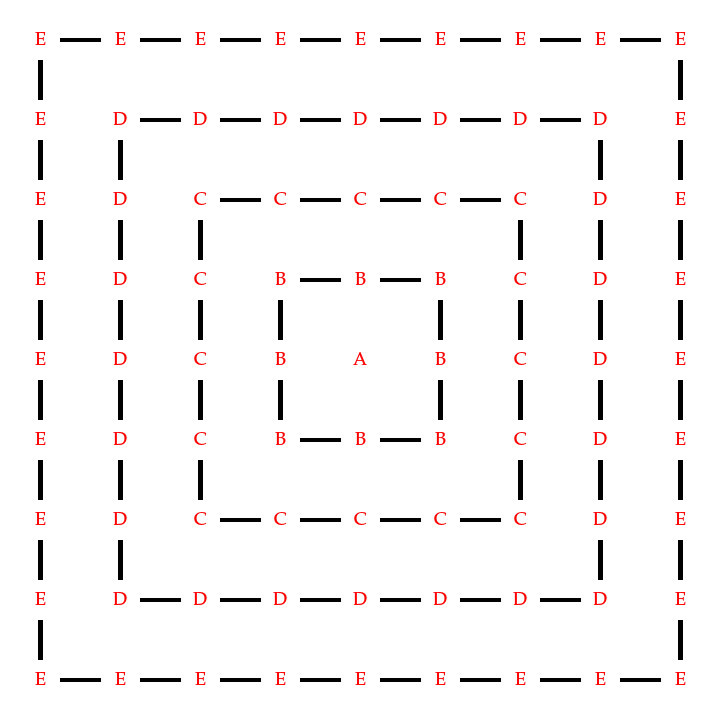
跳晚们打算再加几根导线将某些中继器连接起来.凭借发达的重工业，他们能生产出无数条导线。但由于主板的限制，他们的导线只能和主板四周的边平行，且其长度只够连接相邻两个中继器。

现在他们想知道，他们改造的三星 note7 的电源正极流出的电流能在多短的时间到达电源负极从而造成短路，这样电池就会释放出巨大的能量摧毁跳蚤国的有生力量了。

请参考输入格式和样例配图来更好地理解题意。

输入格式

第一行一个正整数 nn。

第二行n+1 个正整数 a0,a1,…,an，表示从内到外每层的中继器的延时值，单位为秒。其中，第 i 行第 j 列的中继器的延时值为（1≤i,j≤n）amax(|i−n−1|,|j−n−1|)

输出格式

输出一行一个数表示改造后的最短引爆时间。

C/C++ 输入输出 long long 时请用 %lld。C++ 可以直接使用 cin/cout 输入输出。

样例一

input

1

1 2

output

explanation

这个数据对应的主板如下所示：

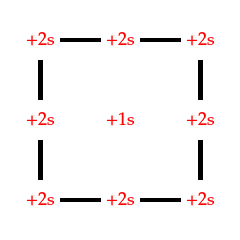
显然，我们可以用导线改造成这样：

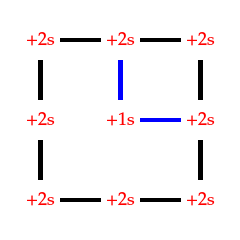
这样从左上角到右下角就会有条 {2,2,1,2,2}{2,2,1,2,2} 的电流路径，耗时为 99 秒。

样例二

input

9

9 5 3 7 6 9 1 8 2 4

output

样例三

见样例数据下载。

限制与约定

测试点编号	nn
1	n≤5n≤5
2	n≤2000n≤2000
3	n≤2000n≤2000
4	n≤5000n≤5000
5	n≤5000n≤5000
6	n≤105n≤105
7
8
9
10

对于所有数据，保证每个数都是不超过 109109 的正整数。

正解：贪心

解题报告：

　　开始的时候直接写了一发50分暴力，就没管了，把后面两道题暴力写完才回过头来看这道题。发现了一些奇怪的贪心，然后就写了。本来T2、T3暴力+骗分分数挺高的，最后A题FST了，仔细看了一下，没开long long...错失虐场机会。

　　考虑一个问题，从外往内数，我们已经到达了第x层，那么1->x-1层每一层都至少经过了一次，否则到不了x。由于图是对称的，我们只考虑一半，另一半直接翻折过去肯定也是最优的。

　　那么我们一定希望决策到x时，之前走过的是最优的情况。如何保证最优性呢？我们记录一下从外往内数前x层的最小的权值，我们肯定希望这一层尽可能地多走，而其他的少走。我们假设走了一层别的层的，我们可以把这个不够优的移动往上平移到最优的那一层走，也就是说我可以在最优的那一层多走一次来代替这一层。可以想到，这样的贪心可以保证到达这一层的花费是最小的。

　　由于到了x之后又会有新的决策，要么再往内走，要么直接从这一层走出去，也就是说不再往内走。后者可以直接通过公式算出来，发现每一层比内一层多4个，所以很快求出直接从这一层走出去的答案。至于前者，可以继续往下做，相当于是进入下一步决策。

 //It is made by ljh2000

 #include <iostream>

 #include <cstdlib>

 #include <cstring>

 #include <cstdio>

 #include <cmath>

 #include <algorithm>

 #include <ctime>

 #include <vector>

 #include <queue>

 #include <map>

 #include <set>

 using namespace std;

 typedef long long LL;

 const int MAXN = ;

 int n;

 LL a[MAXN];

 LL ans,now;

 inline int getint()

 {

     int w=,q=; char c=getchar();

     while((c<'' || c>'') && c!='-') c=getchar(); if(c=='-') q=,c=getchar();

     while (c>='' && c<='') w=w*+c-'', c=getchar(); return q ? -w : w;

 }

 inline void work(){

     n=getint(); for(int i=;i<=n;i++) a[i]=getint();

     now=ans=(1LL<<);  LL lin,tot=;

     for(LL i=n;i>=;i--) {

     lin=a[i]*(*i+)+tot;

     if(lin<ans) ans=lin;

     if(a[i]<now) now=a[i];

     tot+=(now+a[i])*;

     }

     printf("%lld",ans);

 }

 int main()

 {

     work();

     return ;

 }