Backtracking line search的理解

使用梯度下降方法求解凸优化问题的时候，会遇到一个问题，选择什么样的梯度下降步长才合适。

假设优化函数为，若每次梯度下降的步长都固定，则可能出现左图所示的情况，无法收敛。若每次步长都很小，则下降速度非常慢，需要很多轮的迭代，如右图所示。所以步长的选择和收敛速度是一个取舍关系。

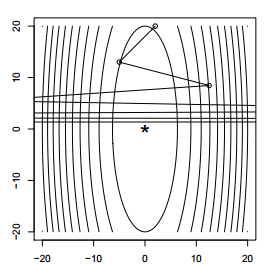
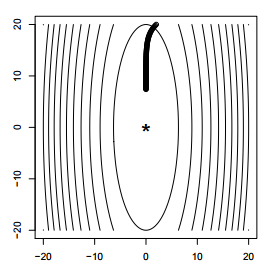
于是，有了一种可调节步长的解法，称为backtracking line search。

假设我们当前的位置为X_c 并且要在d方向上寻找更优的解，那么问题就变为了估计Φ(t)的最小值，t是步长。

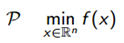
关于P的新的解是。那么怎么来估计这个步长呢？（直接把课件的幻灯片贴上来了）

也就是说，设f(x)在X_c的导数，再设两个变量r和c∈(0, 1).

因为r∈(0, 1)，所以r^v随着v的增大而趋向于0，也就是步长t逐渐减小，直到找到满足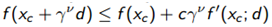条件的r^v。之前已经设定了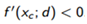，所以必定有

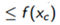
课件里给出了一段Matlab的伪代码，翻译过来差不多就是这样

function t = BLS(f,d,x,r,c)
% Backtracking line search
% Input :
% f: MATLAB file that returns function value
% d: The search direction
% x: current x
% r : backtrack step between (,) usually /
% c: (,) usually ^{-}
% Output :
% t: adaptive step length

[fc, gc] = feval(f,x);
xc = x;
x = xc + t*d;
fk1 = feval(f,x);
t = 1;

while fk1 > fk + c*t*(gk'*d)
    t= t*r; 
    x = xc + t*d; 
    fk1 = feval(f,x); 
end

最后，课件里给出了寻找方向d的几种方法

参考资料：

http://www.stat.cmu.edu/~ryantibs/convexopt/lectures/05-grad-descent.pdf

https://www.math.washington.edu/~burke/crs/408/lectures/L7-line-search.pdf